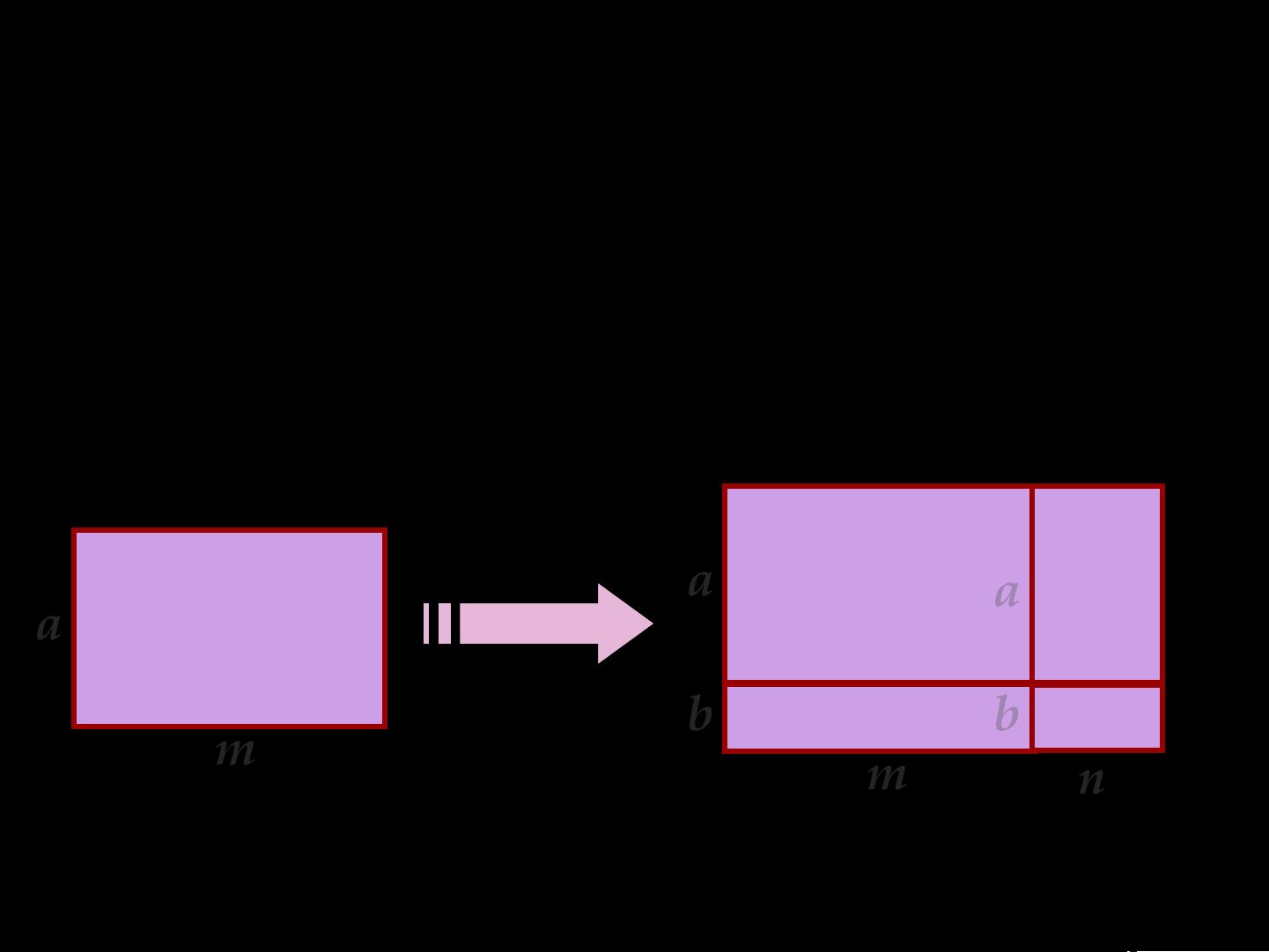
【多项式与多项式相乘】是数学中的一个重要概念，主要涉及代数部分的整式运算。在中学数学教育中，这一部分的知识是基础且关键的。多项式相乘是将两个或多个单项式组合起来形成新的多项式的过程，这个过程涉及到乘法规则和分配律。
我们要明确什么是【单项式】，它是由数字和字母组成的代数表达式，如x、3y等。而【多项式】则是由若干个单项式通过加减运算组合而成的，例如x+2、3x-1等。当两个多项式相乘时，我们需要遵循特定的步骤：
1. **单独乘法**：将每一个单项式分别与另一个多项式的每一项相乘。例如，在计算`(x+2)(x-3)`时，我们需要计算`x*x`、`x*(-3)`、`2*x`和`2*(-3)`。
2. **不遗漏乘法**：确保每个项都被正确地乘过。在上述例子中，我们不能只做`x*x`和`2*x`，还要包括`x*(-3)`和`2*(-3)`。
3. **符号确定**：在乘法过程中，根据乘法规则确定结果的符号。两正得正，两负得正，一正一负得负。例如，`(x+2)(-3x)`中，`x*3x`是正，`2*(-3x)`是负。
4. **合并同类项**：完成所有乘法后，需要将得到的单项式按字母的指数降序排列，并合并相同项。例如，`(x+2)(x-3)`的结果是`x^2 - x - 6`，这里我们合并了`x*x`和`-3x`。
举例来说明：
- **例4**：计算`(x+2)(x-3)`，首先将每一项分别相乘：`x*x`、`x*(-3)`、`2*x`和`2*(-3)`，得到`x^2 - 3x + 2x - 6`，然后合并同类项得到`x^2 - x - 6`。
- **例5**：计算`(2x+5y)(3x-2y)`，同样进行乘法操作后合并同类项，最终得到`6x^2 + x*y - 10y^2`。
在实际应用中，我们可以使用多项式乘法解决实际问题，例如在退耕还林的例子中，通过计算长和宽的变化来确定林区面积的增长。长方形林区原来的面积是`ma`，增长后变为`(m+n)(a+b)`，通过展开多项式得到`ma + mb + na + nb`，证明了面积的增加。
对于给定的随堂练习：
1. `(m+2n)(m-2n)`，这是差平方的形式，展开后为`m^2 - (2n)^2 = m^2 - 4n^2`。
2. `(2n+5)(n-3)`，按照乘法法则计算，得到`2n^2 - 6n + 5n - 15 = 2n^2 - n - 15`。
3. `(x+2y)^2`，这是一个完全平方公式，展开后为`x^2 + 2*2y*x + (2y)^2 = x^2 + 4xy + 4y^2`。
4. `(ax+b)(cx+d)`，这是一般的多项式乘法，计算得到`acx^2 + (ad+bc)x + bd`。
通过这些练习，我们可以更好地理解和掌握多项式相乘的技巧，确保在实际运算中不会出错，并能够灵活运用到更复杂的代数问题中。
