运筹学是一门应用数学学科,它通过使用数学模型来解决实际问题,特别是在管理科学、经济学和工程领域。运筹学中的线性规划是优化问题的一种基本方法,它旨在找到一组决策变量的值,使目标函数达到最大或最小,同时满足一系列线性的约束条件。
线性规划模型通常由以下部分组成:
1. 目标函数:这是我们要最大化或最小化的函数,用 `max` 或 `min` 表示。
2. 约束条件:一组线性的不等式或等式,限制了决策变量的可能取值。
3. 变量:决策变量,它们的值将影响目标函数的结果。变量分为非负变量(`x >= 0`)、无约束变量(`unr`)和非正变量(`x <= 0`)。
4. 标准形式:线性规划模型的标准形式要求目标函数为最大化或最小化,所有约束条件都是等式或不等式,且所有变量都是非负的。
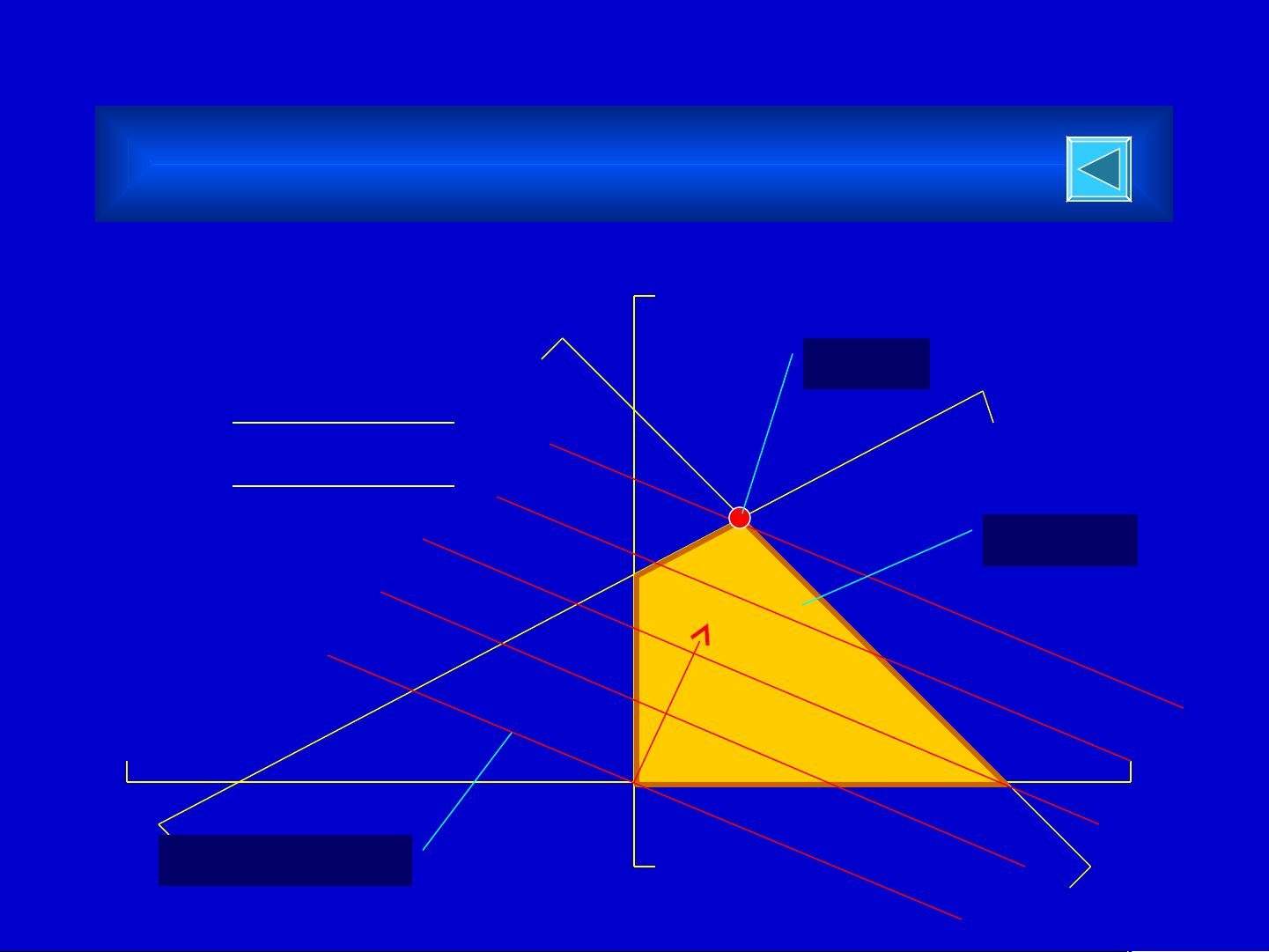
线性规划的图解法是通过绘制目标函数等值线和约束条件的边界来寻找可行域。可行域是所有满足约束条件的决策变量组合形成的区域。对于二维问题,可行域是一个凸集,即任意两点间的线段都在可行域内。在三维或多维问题中,凸集的概念依然适用,只不过可视化较为困难。
线性规划的基本概念包括:
1. 基本解:满足所有约束条件的解,但不一定是可行解。
2. 基础可行解:不仅满足约束条件,而且满足变量的非负约束,表示的是可行域内的一个点。
3. 极点:可行域的顶点,对于凸集来说,线性规划的最优解通常出现在极点上。
4. 基矩阵:由基础变量对应的系数构成的方阵,其行列式不为零。
5. 基变量与非基变量:在基础解中取非零值的变量是基变量,其他变量是非基变量。
单纯形法是一种求解线性规划问题的有效算法,通过迭代过程在不同极点之间转换,寻找目标函数的最佳值。每次迭代涉及选择一个进入基的变量和一个离开基的变量,进行基变换以更新解。这个过程持续进行,直到找到最优解或发现无解或无穷多解。
在实际应用中,运筹学的线性规划广泛用于资源分配、生产计划、运输调度、投资决策等多个领域。通过理解和运用线性规划,我们可以制定更有效的策略,实现资源的最大化利用。