直线裁剪算法研究(Cohen-Sutherland算法和Liang-Barsky算法).doc
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
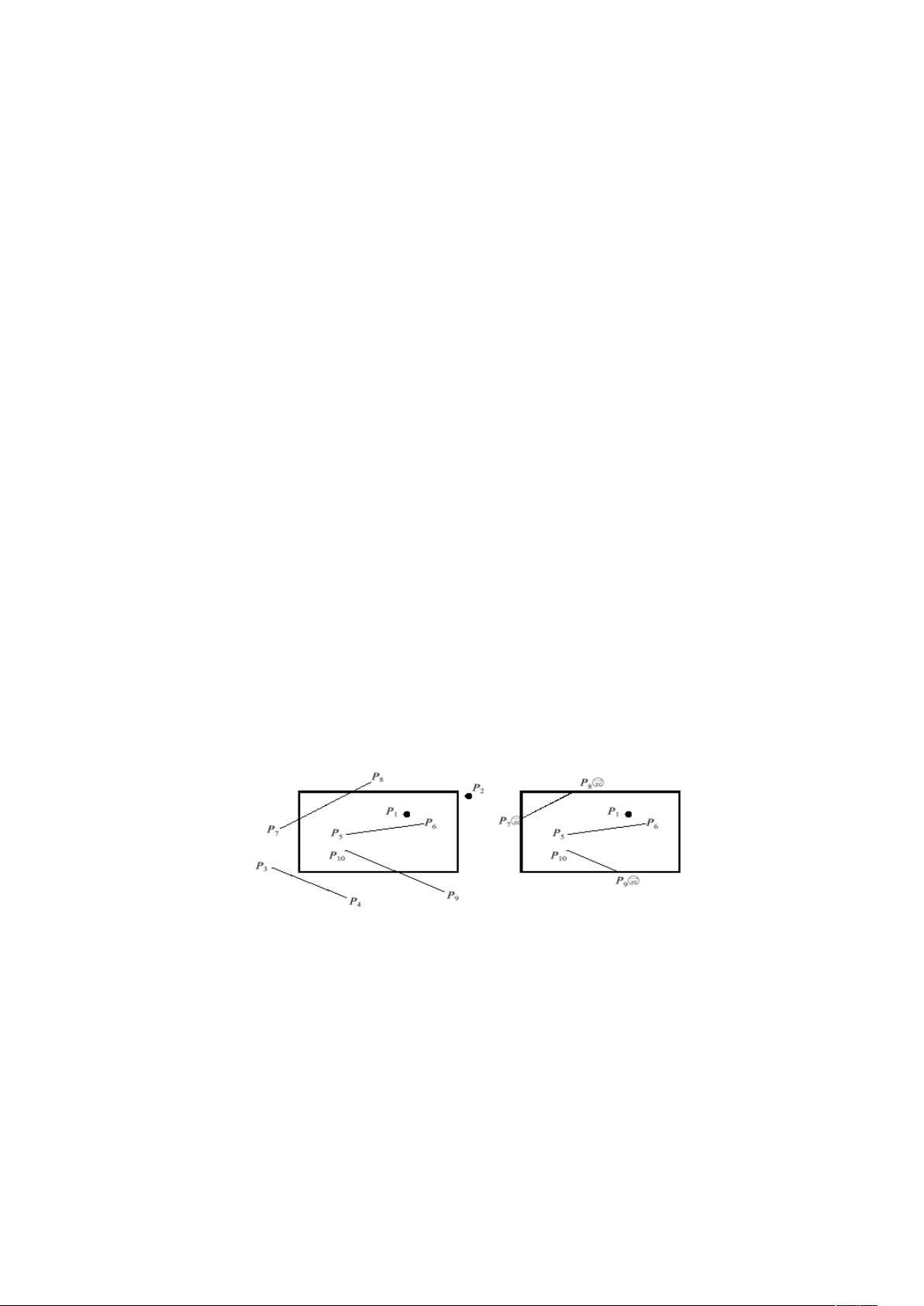
直线裁剪算法研究 本文研究了计算机图形学中的直线裁剪算法,特别是 Cohen-Sutherland 算法和 Liang-Barsky 算法。直线裁剪算法是计算机图形学中的一个重要技术,对于常见的直经线裁剪的算法分析的基础上,针对 Cohen-Sutherland 算法和 Liang-Barsky 算法进行了分析研究。 第一部分:直线裁剪的基本原理 直线裁剪算法的基本原理是检查直线的两个端点是否在窗口之内,确定如何对此直线裁剪。如果一条直线的两个端点均在窗口之内,则此直线应保留。如果一条直线的一个端点在窗口外,另一个点在窗口内,则应从直线与边界的交点处裁剪掉边界之外的线段。如果直线的两个端点均在边界外,则可分为两种情况:一种情况是该直线全部在窗口之外;另一种情况是直线穿过两个窗口边界。 第二部分:Cohen-Sutherland 算法 Cohen-Sutherland 算法的核心是把所有直线的端点均分配一个表示其相对位置的 4 位二进制代码,即区域码。区域码按照端点与窗口边界的相对位置编码,即区域码的 4 位分别代表端点位于窗口的上、下、左、右。区域码从右到左的各位所代表的坐标区如下所示: 位 4 3 2 1 坐标区 上 下 右 左 上述各位中某位为 1,则表示点位于此坐标区。窗口周围各坐标区的区域码如图 2 所示。由图 2 可见,位于窗中内的点,其区域码应为 0000,位于窗口左下方的点,其区域码应为 0101,其余类推。 第三部分:Liang-Barsky 算法 Liang-Barsky 算法是另一种常见的直线裁剪算法。该算法的基本思想是将直线切割成多个小段,然后检查每个小段是否在窗口之内。如果小段在窗口之内,则保留该小段;否则,裁剪掉该小段。 第四部分:比较分析 本文对 Cohen-Sutherland 算法和 Liang-Barsky 算法进行了比较分析。结果表明,Cohen-Sutherland 算法的计算速度较快,但需要更多的存储空间;Liang-Barsky 算法的计算速度较慢,但需要较少的存储空间。 本文对直线裁剪算法进行了详细的研究,特别是 Cohen-Sutherland 算法和 Liang-Barsky 算法的分析研究。这两种算法都是计算机图形学中的重要技术,对于常见的直经线裁剪的算法分析的基础上,进行了分析研究。这将有助于计算机图形学的发展和应用。

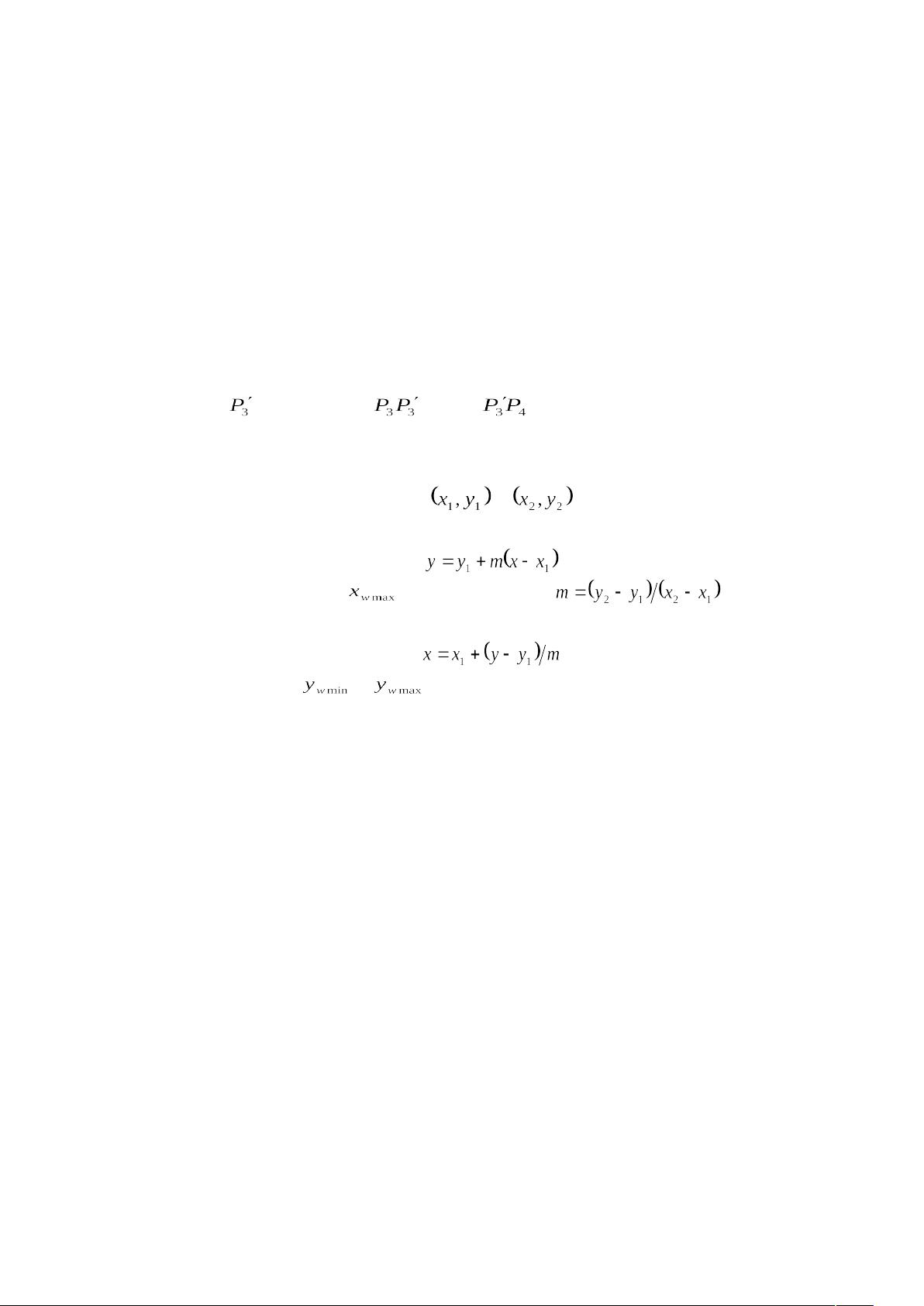
剩余10页未读,继续阅读

- 粉丝: 92
- 资源: 2万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- (源码)基于Maven + MyBatis的图书管理系统.zip
- 2024 年 10 月 26 日,第 19 届中国 Linux 内核开发者大会于湖北武汉成功举办 来自全国各地的近 400 名内核开发者相约华中科技大学,聆听讲座,共商 Linux 内核未来之发展12
- (源码)基于C++的仓储盘点系统.zip
- linux常用命令大全
- mongodb-compass-1.44.6-darwin-x64.dmg
- (源码)基于JavaFX和MyBatis的HSY寝室管理系统.zip
- 对AVEC2014视频进行Dlib或MTCNN人脸裁剪
- excel数据分析案例1数据
- 调试版_蓝牙串口APP.apk
- (源码)基于Spring Boot和Vue的基金管理系统.zip


 信息提交成功
信息提交成功