没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

第 07 讲 反馈网络

反馈网络 (Recurrent Network) ,又称自联想记忆网络,其
目的是为了设计一个网络,储存一组平衡点,使得当
给网络一组初始值时,网络通过自行运行而最终收敛
到这个设计的平衡点上。
1982 年,美国加州工学院物理学家霍普菲尔德 (J . Hopf
ield) 发表了一篇对人工神经网络研究颇有影响的论文。
反馈网络能够表现出非线性动力学系统的动态特性。它
所具有的主要特性为以下两点:
第一、网络系统具有若干个稳定状态。当网络从某一初
始状态开始运动,网络系统总可以收敛到某一个稳定
的平衡状态;
第二,系统稳定的平衡状态可以通过设计网络的权值而
被存储到网络中。

在本章中,我们将集中讨论反馈网络,通过网络神经元
状态的变迁而最终稳定于平衡状态,得到联想存储或
优化计算的结果。
在这里,着重关心的是网络的稳定性问题,研究的重点
是怎样得到和利用稳定的反馈网络。
霍普菲尔德网络是单层对称全反馈网络,根据其激活函
数的选取不同,可分为离散型的霍普菲尔德网络 (Discr
ete Hopfield Neural Network ,简称 DHNN) 和连续型的
霍普菲尔德网络 (Continuous Hopfield Neural Network ,
简称 CHNN) 。
DHNN 的激活函数为二值型的,其输入、输出为 {0 , 1}
的反馈网络,主要用于联想记忆。
CHNN 的激活函数的输入与输出之间的关系为连续可微
的单调上升函数,主要用于优化计算。
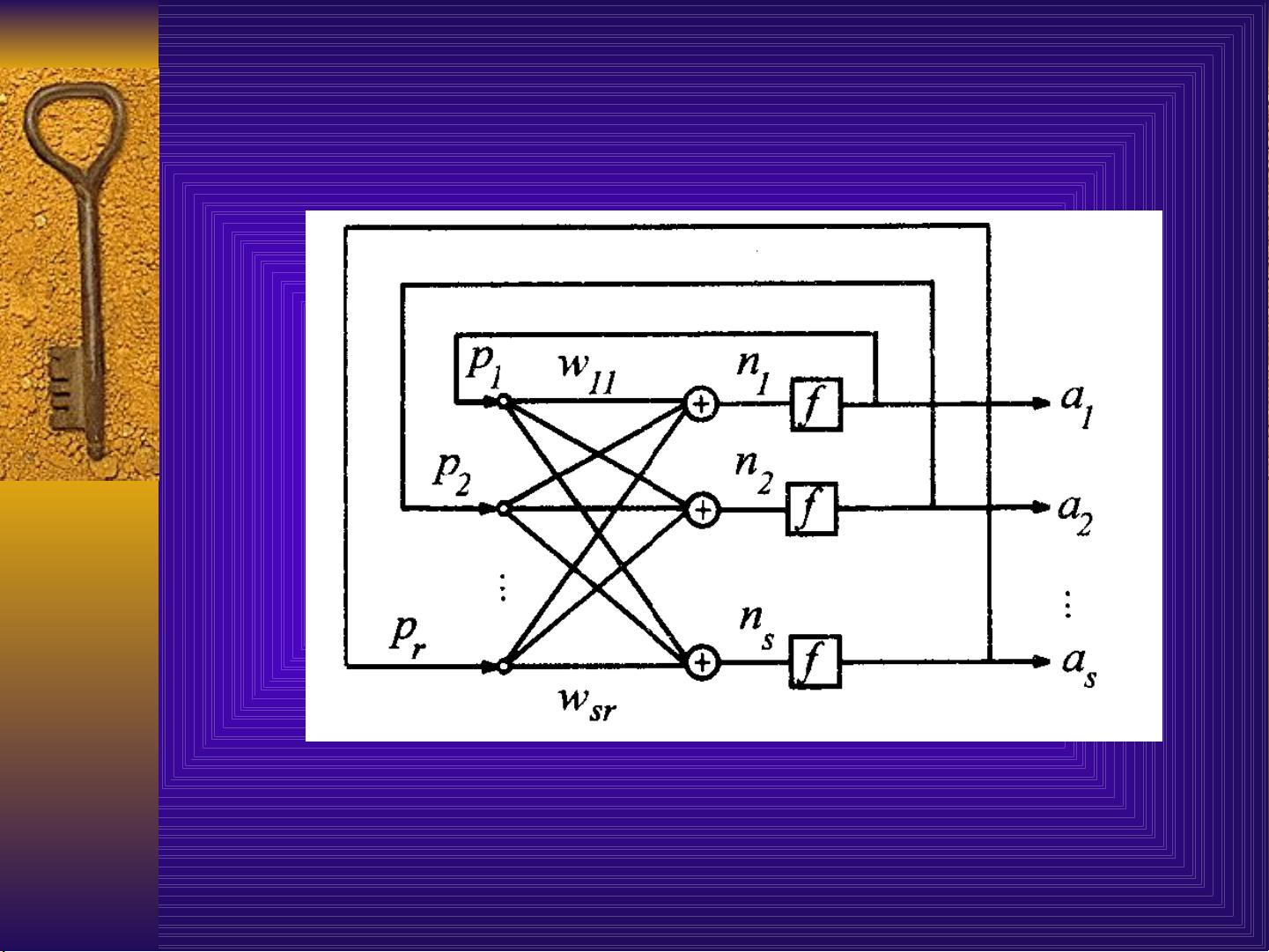
7 . 1 霍普菲尔德网络模型
图 7 . 1 反馈网络结构图

在反馈网络中
如果其激活函数 f(·) 是一个二值型的硬函数,如图 7 . 2 所
示,即 a
i
= sgn(n
i
) , i = l, 2, … r ,则称此网络为离散型
反馈网络;
如果 a
i
=f(n
i
) 中的 f(·) 为一个连续单调上升的有界函数,这
类网络被称为连续型反馈网络。图 7 . 3 中所示为一个
具有饱和线性激活函数,它满足连续单调上升的有界函
数的条件,常作为连续型的激活函数。
图 7 . 2 DHNN 中的激活函数 图 7 . 3 CHNN 中的激活函数
剩余41页未读,继续阅读
资源评论

wei.yinfu
- 粉丝: 9
- 资源: 22
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功