2013数学建模B题附件四答案代码顺序

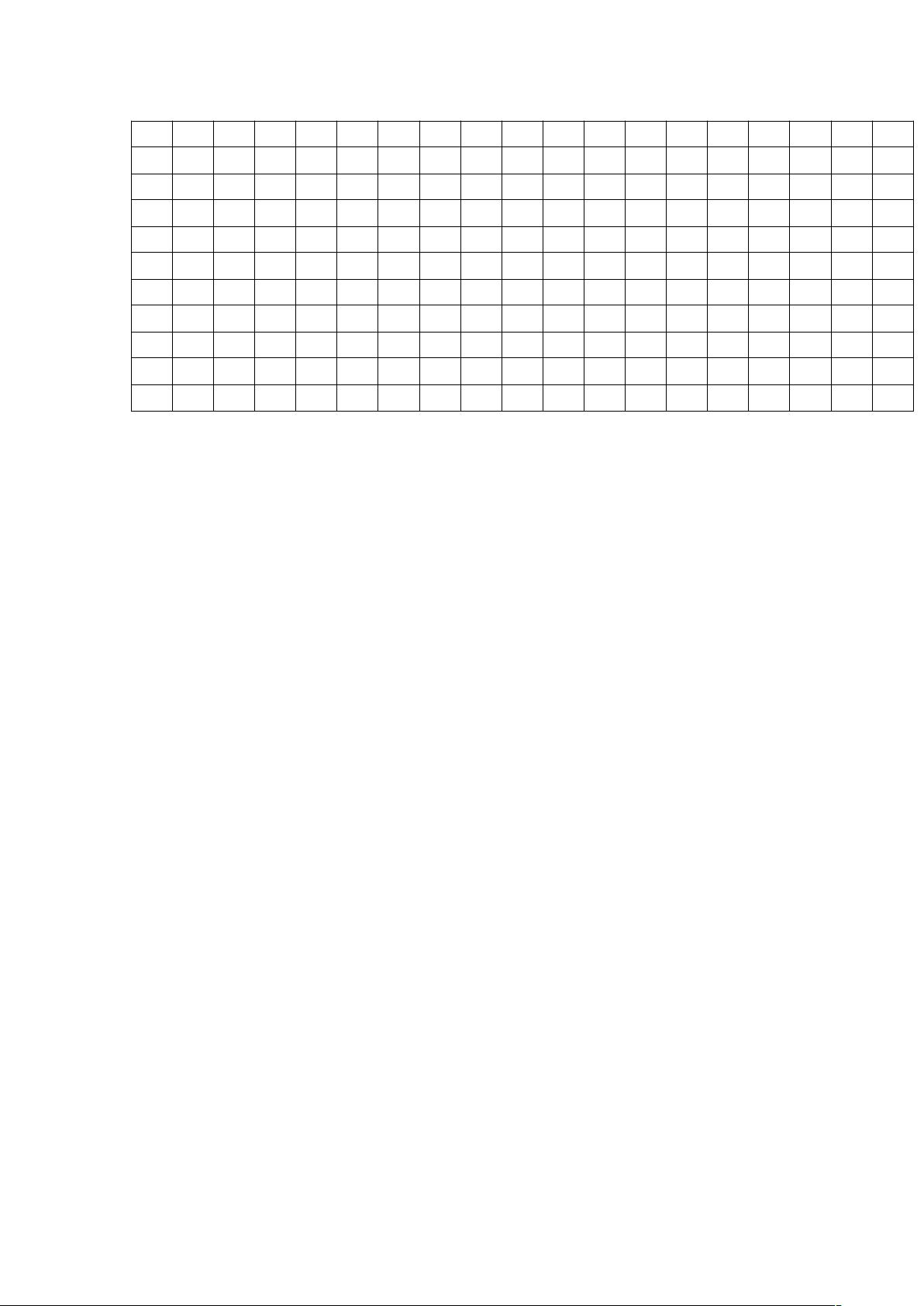
(1) 附件1、附件2的结果：将碎片序号按复原后顺序填入1×19的表格； (2) 附件3、附件4的结果：将碎片序号按复原后顺序填入11×19的表格； (3) 附件5的结果：将碎片序号按复原后顺序填入两个11×19的表格； (4) 不能确定复原位置的碎片，可不填入上述表格，单独列表。 在2013年的数学建模竞赛中，B题涉及到了一种基于碎片复原的问题，这个问题需要参赛者处理一系列的数据并进行序列排列。这道题目要求参赛者对给出的附件进行分析，然后按照特定的顺序将碎片序号填充到不同的表格中。 我们需要理解描述中的四个关键点： 1. **附件1和附件2的结果**：这两个附件提供的数据需要被整合到一个1×19的表格中。这意味着参赛者需要找到19个碎片，并按照复原后的正确顺序将它们的序号填入这个单一列的表格。 2. **附件3和附件4的结果**：这两个附件的数据需要填充到一个11×19的表格中。这可能意味着存在更复杂的排列，每个附件提供了19个碎片，但它们分别对应于11行的不同位置。 3. **附件5的结果**：这个附件的数据涉及到两个11×19的表格。这表明存在两种不同的排列情况，每个表格都需要有11行，每行包含19个碎片，总计38个碎片。 4. **未确定位置的碎片**：对于无法确定复原位置的碎片，它们不需要填入上述表格，而是应该单独列出。这可能是为了区别处理，以便后续分析或者寻找额外线索来确定其位置。 从部分内容来看，我们看到了一串数字序列，这些数字很可能是碎片的序号。例如，191075011154190184002104180064106004149032204065039067147等，这些序号需要根据附件中的信息进行排序和归位。 在解决这类问题时，参赛者可能需要运用数学、逻辑推理和计算机编程等技能。他们可能需要利用数据结构（如数组或列表）来存储碎片序号，使用排序算法（如冒泡排序、快速排序或归并排序）对碎片进行排序，以及通过矩阵操作来构建和填充表格。此外，数据分析和模式识别也至关重要，因为碎片的排列可能隐藏着某种规律或模式。 对于不确定位置的碎片，可能需要使用概率论或模糊逻辑的方法来推测它们可能的位置，或者通过与其他碎片的关联性来逐步确定。同时，建模过程可能涉及到迭代和优化，以逐步改善复原的准确性和完整性。 2013年数学建模B题考察了参赛者处理复杂数据、建立数学模型、编程实现和逻辑推理的能力，是一道综合性的挑战。通过这样的问题，学生能够提升解决实际问题的技能，并学习如何将理论知识应用到实践中。