没有合适的资源?快使用搜索试试~ 我知道了~
资源详情
资源评论
资源推荐

第一讲:程序语言的发展过程
任务:以程序为对象,分析其属性,如:
值的获取与传播,活跃性
应用:程序转换 程序理解 程序演化 程序逆
向工程 程序验证与测试 程序优化 重构 自
动并行化
发展:
机器语言:
指令:
二进制组成
具有基本操作,左移、右移、加 1
缺点:
可读性差(可理解性差)
写程序困难(不方便)
问题:程序的维护比较困难
扩展 纠错 预防 适应
汇编语言:
符号化了的机器语言
功能没有扩充
可读性强
高级程序设计语言:
(1)过程( PASCAL,C,FORTRAN,PL1)
特点:命令为基础,程序由一系列语句组
成,语句的执行引起存储单元值的变化。
程序的正确型(归纳断言指导…)
数学性质弱(副作用,变量值变化)
数据类型不够丰富
程序的动静态结构差异大
Goto 语言的争议(难以理解,难以查错,
动静态差异大
修改引起的副作用小,全局优化简单
概念简单,效率高)
(2)函数式语言(LISP,ML,HOPE,FP)
程序由一组函数组成,通过调用执行程序。
特点:
数学性质好
数据类型可自定义
支持并行计算
抽象级别高
数据以表为基础
(3)逻辑式语言(PROLOG)
以谓词为基础,具有推理能力
特定的应用领域抽象的问题求解公式处理
专家系统人工智能等
(4)对象式语言 SmallTalk80
特点:封装性 继承性 多态性
第四代语言:特定领域的特殊类语言 高级
语 言 的 抽 象 如 : Oracle 应 用 开 发 环 境 、
Power Builder…
程序分析方法:
静态分析方法:(词法分析 语法分析 所需
要的分析)
动态分析方法
第二讲:编译原理基础
基本概念:
• 字母表: ∑,元素的非空有穷集合。
• 符号串:由字母表中的符号组成的
任何有穷序列。或者如下定义:
1. 空符号串 ε 是 S 上的符号串
2. 若 x 是 S 上的符号串,a 是 S
的元素,则 xa 是 S 上的符号
串
3. y 是 S 上的符号串,当且仅
当它可以由 1 和 2 导出
• 符号串的连接:设 x 和 y 均是字母
表∑上的符号串,它们的连接是把
y 的所有符号顺序接在 x 的符号之
后所得到的符号串。
• 符号串的方幂:设 x 是字母表∑上
的符号串,把 x 自身连接 n 次得到
的符号串 z, 称作符号串 x 的 n 次幂,
记作 z=(幂形式) ,特别地:x0=e
• 前缀和后缀:设 x 是字母表上的符
号串,x=yz ,则 y 是 x 的前缀,z 是
x 的后缀,特别是当 z≠e 时,y 是 x
的真前缀;y≠ε 时,z 是 x 的真后
缀。
• 子字符串:非空字符串 x ,删去它的
前缀和后缀后所得到的字符串称为
x 的子字符串,简称子串。如果删
去的前缀和后缀不同时为 ε,则称该
子串为真子串。
• 符号串集合:若集合 A 中的所有元
素都是某字母表上的符号串,则称
A 为该字母表上的符号串集合。
• 符号串集合的乘积:设 A、B 是两
个符号串集合,AB 表示 A 与 B 的
乘积,则定义
AB={xy|(x∈A)∧(y∈B)}
• 符号串集合的方幂:设 A 是符号串
集合,则称 A
i
是符号串集合 A 的
方幂,其中 i 是非负整数。
A
0
={e}, A
1
=A, A
2
=AA, …, A
n
=AA… A
• 符 号 串 集 合 的 正 闭 包 :
A
+
=A1∪A2∪A3 …
• 符 号 串 集 合 的 星 闭 包 : A*=
A0∪A1∪A2∪A3 …
2 正则表达式
• 定义:RE 为定义在∑上的正则表达
式则
– ∧,ε∈RE
– 若 a∈∑,则 a∈RE
– 若 e1,e2∈RE , 则 e1·e2,e1|
e2,e1
+
∈RE
• 语义函数(解释函数)L
L(∧)=Ф,L(ε)={ε}
– 若 a ∈ ∑则 L(a)={a}
– 若 e1,e2∈RE 则 L(e1·e2)=
L(e1)·L(e2) L(e1|e2)=
L(e1)∪L(e2) L(e1
+
)= L
+
(e1)
Eg:ab
*
表示所有以字母 a 开头的后面跟了 n
个(包括)0 个 b 的字符串
a(a|b)
*
表示所有以 a 开头的字符串
3 自动机 定义:一个 DFA 是一个 5 元组
(S,∑,δ,S
0
,F),其中 S 是状态集合,∑是字符
集 , δ 是转 换 函数 (转 移函 数) S×∑→S
,S
0
为初始状态 S
0
∈S,F 为终止状态集合,
F⊆S。
两种表示形式 ( 转换图 转换矩阵)
Eg: 确定有限状态自动机 M=({a, b},
{S, U, V, Q}, f, S, {Q}),其中 f 定义为:
f (S, a)=U f (V, a)=U
f (S, b)=V f (V, b)=Q
f (U, a)=Q f (Q, a)=Q
f (U, b)=V f (Q, b)=Q
S U V Q
a U Q U Q
b V V Q Q
S U V Q
a U Q U Q
b V V Q Q
S U
QV
a
a
a
b
b
b
词法分析:
功能:读源程序的字符序列,逐个拼出单
词,并构造相应的内部表示,同时检查源
程序中的词法错误。
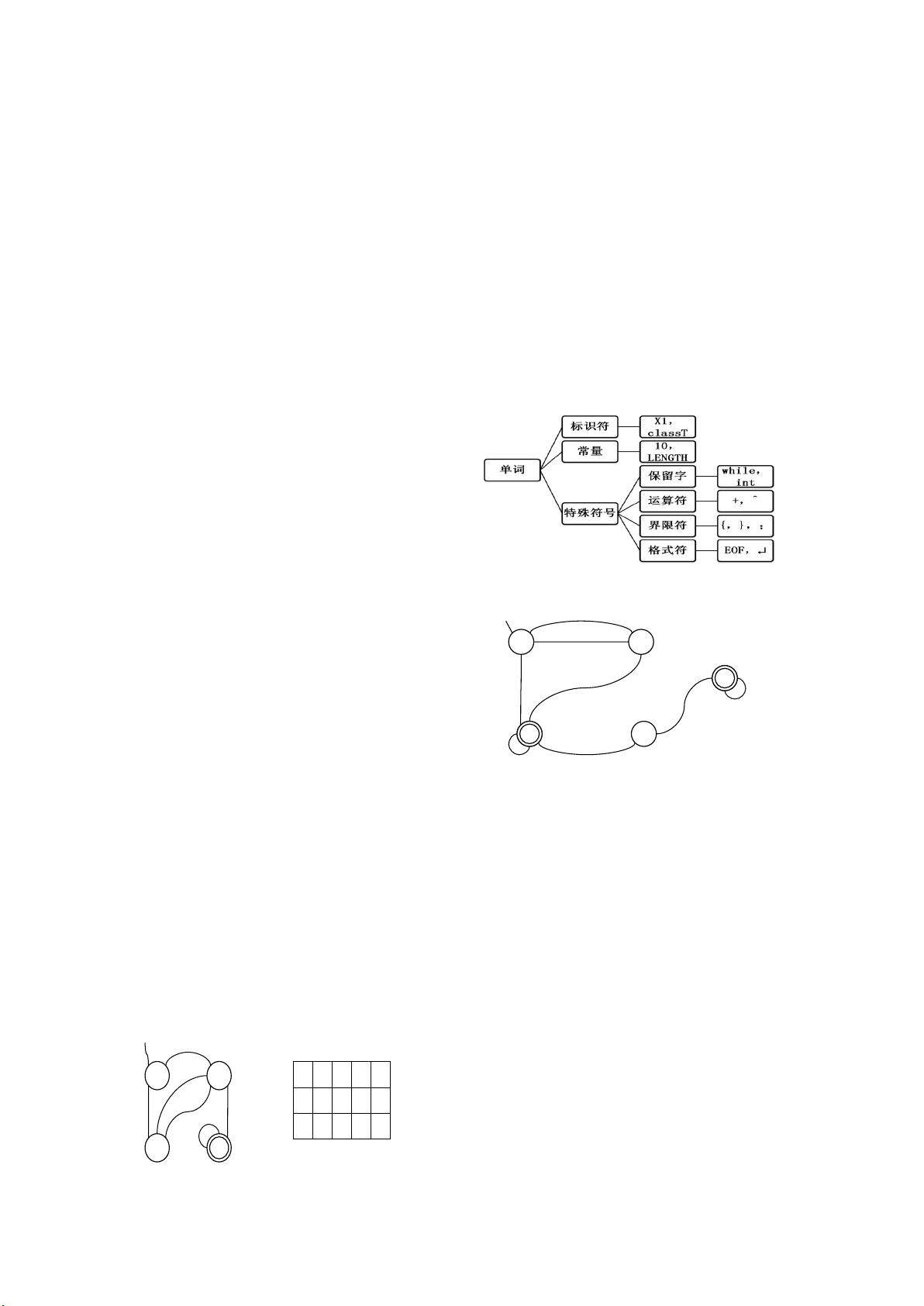
单词:所谓单词是指语言中具有独立含义
的最小的语义单位。
Token:单词的内部表示。“程序语言的操
作对象( 只能)是该语言规 定的各种数
据。”编译程序是用某种程序语言书写的程
序,其操作对象是一般程序中的各种语法
单位。
单词的一种分类:
识别常数的自动机
13
A B
EE
+
数字
-
数字
数字
CC
数字
D
小数点
数字
注:未考虑前导0的情形
文法概述
定义
文法 G 定义为四元组(V
T
,V
n
,S,P)
V
T
是有限的终极符集合
V
n
是有限的非终极符集合
S 是开始符,SÎ V
n
P 是产生式的集合,且具有下面的形式:
aàb,其中 a,bÎ (V
T
UV
n
)*
分类
• O 型文法:也称为短语文法,其产
生式具有形式: a→b,其中 a,bÎ
(V
T
ÈV
N
)*,并且 a 至少含一个非终
极符 。
• 1 型文法:也称为上下文相关文法
它是 0 型文法的特例,要求|a| £ |b|
(S→l 例外,但 S 不得出现于产生

式右部)。
• 2 型文法:也称为上下文无关文法
它是 1 型文法的特例,即要求产生
式左部是一个非终极符: A→b 。
• 3 型文法:也称为正则文法。它是
2 型文法的特例,即产生式的右部
至多有两个符号,而且具有下面形
式之一: A →a ,A →a B 其 中
A,BÎ V
N
,aÎ V
T
。
• 推导(直接推导):如果 Ab ®是一
个产生式,则有 aAgbaÞg ,其中 Þ
表示一步推导(用 A →b)。这时称
gba 是由 aAg 直接推导的。
Þ 的含义是,使用一条规则,代替 Þ
左边的某个符号,产生 Þ 右端的符号串。
• a Þ+ b: 表示 a 通过一步或多步可
推导出 b
• a Þ* b : 表示 a 通过 0 步或多步可
推导出 b
• 句型:如果有 SÞ* b ,则称符号串
b 为 CFG 的句型 。我们用 SF(G)表
示文法 G 的所有句型的集合。
• 句子:如果 b 只包含终极符,则称
b 为 CFG 的句子。
• 语言:L(G)={ u| S Þ+ u ,u Î VT* }
文法 G 所定义的语言是其开始符所能推导
的所有终极符号串(句子)的集合。
最左(右)推导:如果进行推导时
选择的是句型中的最左(右)非终极符,则
称这 种 推 导 为最 左 ( 右) 推 导 , 并用符号
lm(rm)表示最左(右)推导。
左(右)句型:用最左推导方式导
出的句型,称为左句型,而用最右推导方
式导出的句型,称为右句型(规范句型)。
结论:每个句子都有相应的最右和
最左推导(但对句型此结论不成立)
• 短语:设 S 是文法的开
始 符 , bpa 是 句 型 ( 即 有 S
Þ*bpa),如果满足条件:
SÞ* aAb AÞ+ p pÎV
T
+
则称 p 是句型 bpa 的一个短语。
任一子树的树叶全体(具有共同祖先的叶节
点符号串)皆为短语。
• 直 接 短语( 简 单 短语)
如果满足条件:
SÞ* aAb AÞ p pÎV
T
+
则称 p 是句型 bpa 的一个简单短
语。 任一简单子树的树叶全体(具有共同父
亲的叶节点符号串)皆为简单短语。
• 句柄:一个句型可能有
多个简单短语,其中最左的简单短
语称之为句柄。
• 语法分析树(简称分析树)
用来描述句型的结构,是句型推导
的 一 种 树 型 表 示 。 文 法
G=(V
N
,V
T
,S,P),则称满足下面条件
的树为 G 的一棵语法分析树:
• 每 个 结 点 都 有
G 的一个文法符号,并且
根结点标有初始符 S,非叶
结点标有非终极符,叶结
点标有终极符或非终极符
或 l。
• 如 果 一 个 非 叶
结点 A 有 n 个儿子结点(从
左到右)为 X1,X2,...,Xn,
则 G 一 定 有 产 生 式
A→X1X2 ...Xn 。
• 线性推导:我们称用 Þ
符号进行的推导为线性推导 。
• 树型推导与线性推导的
不同:线性推导指明了推导的顺序
而树型推导则没有指明推导的顺序
因此,句型一般只有一棵分析树(如
果无二义性),而线性推导则可以有
很多棵分析树。
• 二义性文法:如果一个
文法的某个句型有两棵不同的语法
分析树,则称该文法二义性为二义
性文法。
例:文法 G=( {+,*,i,(,)}, {E}, E, P),
其中 P 为:
E ® i E ® E + E
E ® E * E E ® ( E )
剩余10页未读,继续阅读
奋斗小英雄
- 粉丝: 6
- 资源: 16
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功


评论7