Delta 机器人反解算法
Delta 机器人反解算法是指通过数学模型和算法来确定机器人的关节角度和位置,以便控制机器人的运动。该算法是机器人学和计算机视觉领域中的一个基本问题。
Kinematics Analysis of a Delta Parallel Robot
Delta 机器人是一种特殊的平行机器人,它由三个平行臂组成,每个臂都连接着一个滑块,滑块上安装着一个电机。 Delta 机器人的反解算法是指通过数学模型和算法来确定机器人的关节角度和位置,以便控制机器人的运动。
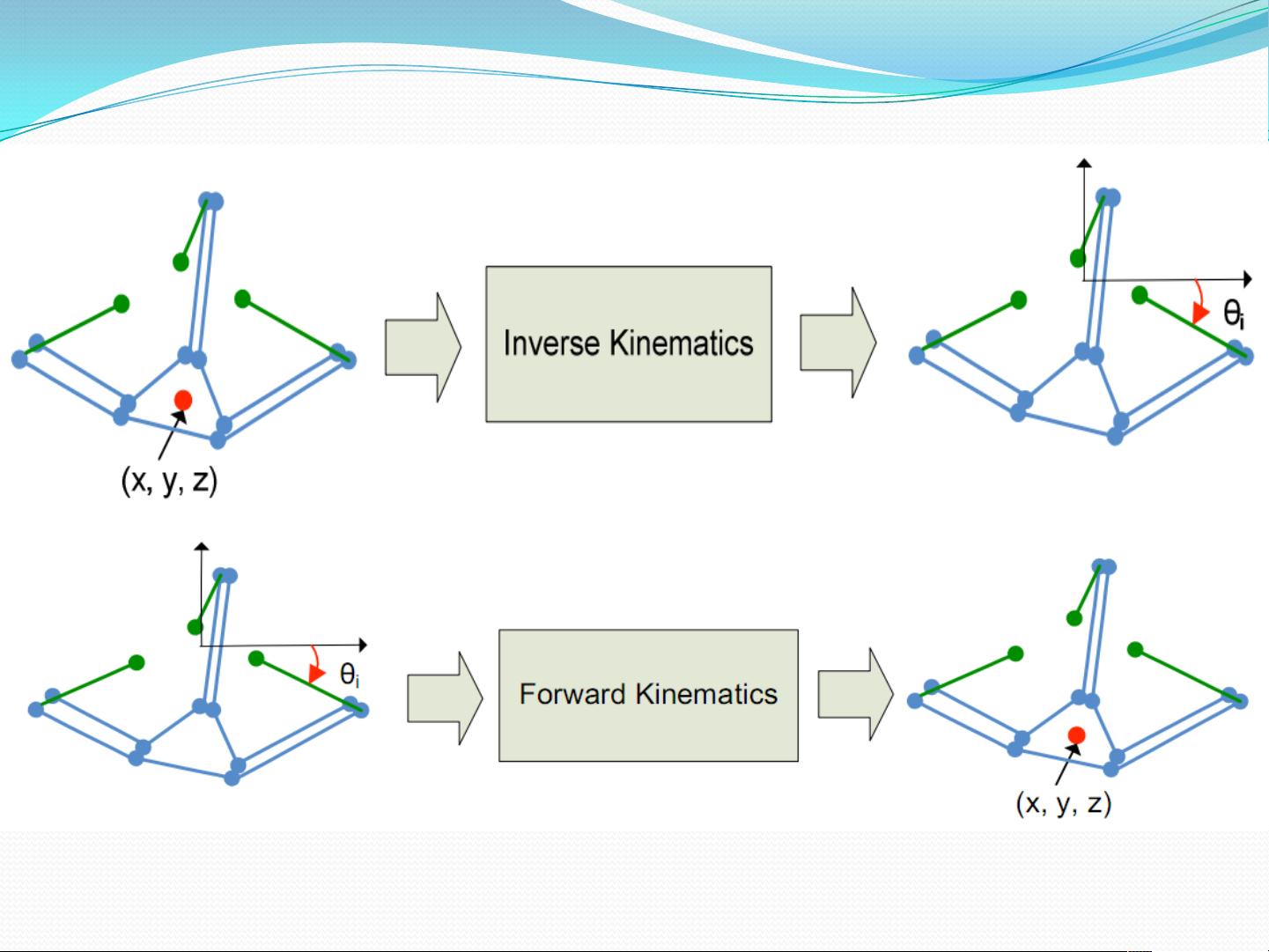
Inverse Kinematics (IK)
逆解算法是机器人学中一个基本问题,它指的是通过机器人的末端执行器的位置和姿态来确定机器人的关节角度。逆解算法的目的是为了使机器人能够准确地执行任务,例如抓取物体、焊接等。
Delta 机器人的逆解算法可以通过以下步骤来实现:
1. 建立数学模型:建立 Delta 机器人的数学模型,包括机器人的几何参数和运动学参数。
2. 确定末端执行器的位置和姿态:通过传感器或其他方法确定机器人的末端执行器的位置和姿态。
3. 求解逆解算法:使用数学模型和末端执行器的位置和姿态来求解机器人的关节角度。
Forward Kinematics (FK)
正解算法是机器人学中另一个基本问题,它指的是通过机器人的关节角度来确定机器人的末端执行器的位置和姿态。正解算法的目的是为了使机器人能够准确地执行任务,例如抓取物体、焊接等。
Delta 机器人的正解算法可以通过以下步骤来实现:
1. 建立数学模型:建立 Delta 机器人的数学模型,包括机器人的几何参数和运动学参数。
2. 确定机器人的关节角度:确定机器人的关节角度。
3. 求解正解算法:使用数学模型和机器人的关节角度来求解机器人的末端执行器的位置和姿态。
Multiply Pci with the rotational matrix
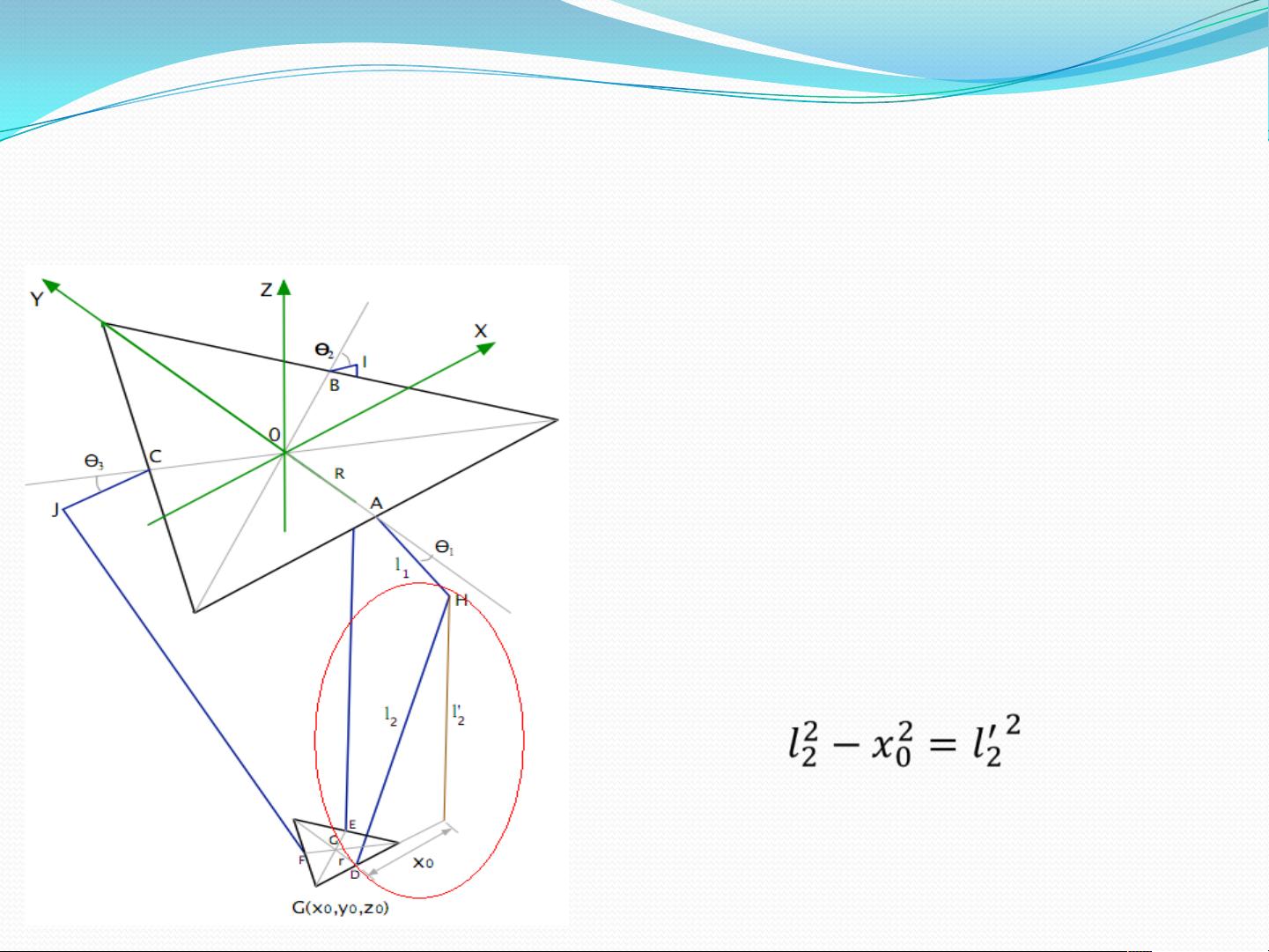
在 Delta 机器人的反解算法中,需要将机器人的关节角度与旋转矩阵相乘,以便求解机器人的末端执行器的位置和姿态。
Three ball equations as:
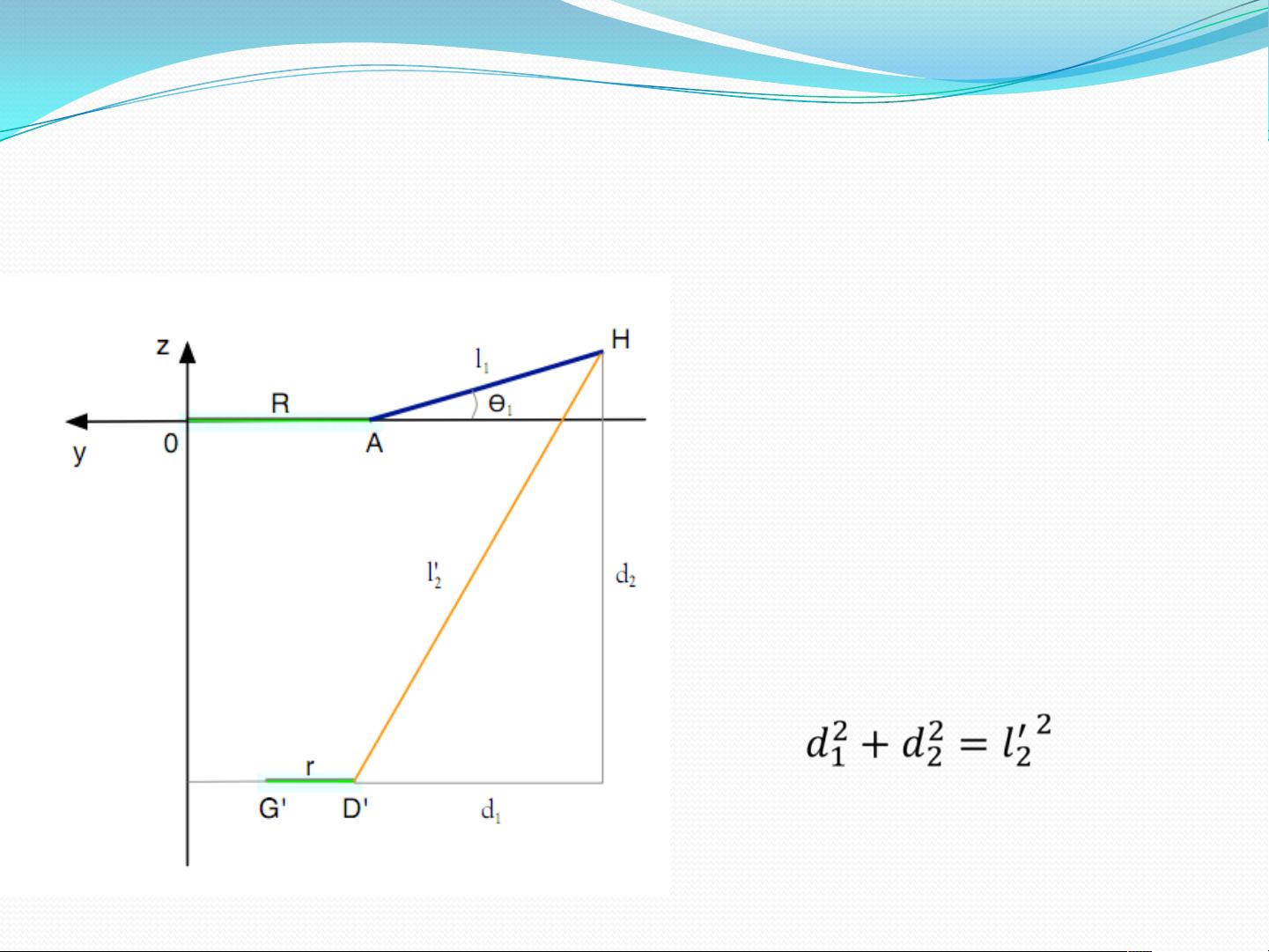
在 Delta 机器人的反解算法中,需要使用三个球面方程来描述机器人的运动。这些方程可以描述机器人的末端执行器的位置和姿态。
Two solutions : z > 0, z < 0
在 Delta 机器人的反解算法中,可能存在两个解决方案,即 z > 0 和 z < 0。这两种解决方案对应着机器人的两个可能的运动状态。
√√x
在 Delta 机器人的反解算法中,需要使用平方根和其他数学操作来求解机器人的关节角度和位置。
Test & Verify in Matlab
在 Delta 机器人的反解算法中,需要使用 Matlab 等软件来测试和验证算法的正确性。
DeltaRobotForward(-18,13,30,235,800,200,45)
这是一段 Matlab 代码,用于测试和验证 Delta 机器人的反解算法。
z = -703.0740, x = 80.7752, y = -200.2409
这些是 Delta 机器人的反解算法的结果,它们描述了机器人的末端执行器的位置和姿态。