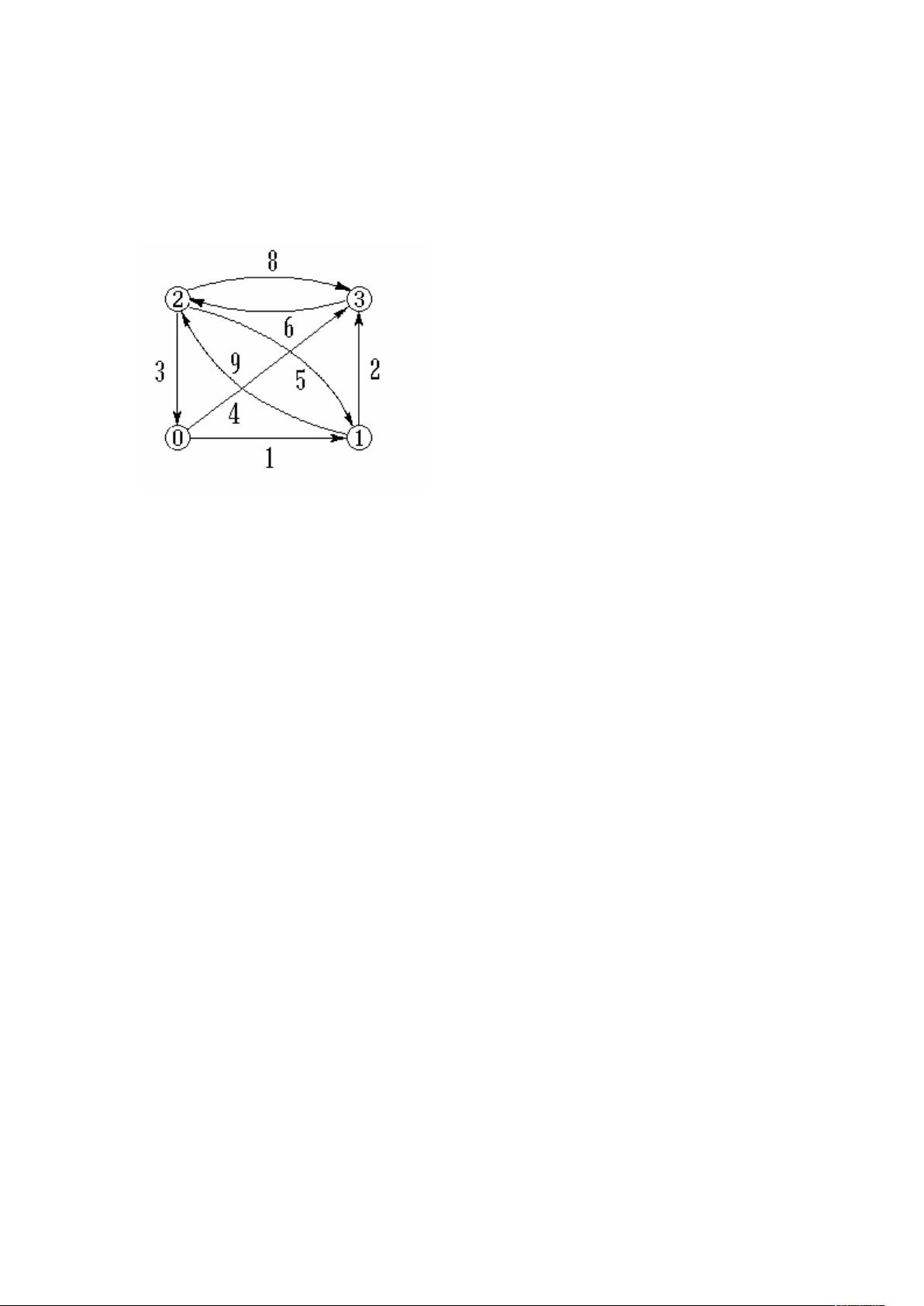
实现图的遍历算法 深度优先遍历

2． 系统设计 1．用到的抽象数据类型的定义 图的抽象数据类型定义： ADT Graph{ 数据对象V：V是具有相同特性的数据元素的集合，称为顶点集 数据关系R： R={VR} VR={<v,w>|v,w∈V且P(v,w),<v,w>表示从v到w的弧， 谓词P(v,w)定义了弧<v,w>的意义或信息} 基本操作P： CreatGraph(&G,V,VR) 初始条件：V是图的顶点集，VR是图中弧的集合 操作结果：按V和VR的定义构造图G DestroyGraph(&G) 初始条件：图G存在 操作结果：销毁图G InsertVex(&G,v) 初始条件：图G存在，v和图中顶点有相同特征 操作结果：在图G中增添新顶点v …… InsertArc(&G,v,w) 初始条件：图G存在，v和w是G中两个顶点 操作结果：在G中增添弧<v,w>，若G是无向的则还增添对称弧<w,v> …… DFSTraverse(G,Visit()) 初始条件：图G存在，Visit是顶点的应用函数 操作结果：对图进行深度优先遍历，在遍历过程中对每个顶点调用函数Visit一次且仅一次。一旦Visit()失败，则操作失败 BFSTraverse(G,Visit()) 初始条件：图G存在，Visit是顶点的应用函数 操作结果：对图进行广度优先遍历，在遍历过程中对每个顶点调用函数Visit一次且仅一次。一旦Visit()失败，则操作失败 }ADT Graph 栈的抽象数据类型定义： ADT Stack{ 数据对象：D={ai|ai∈ElemSet,i=1,2,…,n,n≥0} 数据关系：R1={<ai-1,ai>|ai-1,ai∈D,i=2,…,n} 约定an端为栈顶，ai端为栈底 基本操作： InitStack(&S) 操作结果：构造一个空栈S DestroyStack(&S) 初始条件：栈S已存在 操作结果：将S清为空栈 StackEmpty(S) 初始条件：栈S已存在 操作结果：若栈S为空栈，则返回TRUE，否则FALSE …… Push(&S,e) 初始条件：栈S已存在 操作结果：插入元素e为新的栈顶元素 Pop(&S,&e) 初始条件：栈S已存在且非空 操作结果：删除S的栈顶元素，并用e返回其值 StackTraverse(S,visit()) 初始条件：栈S已存在且非空 操作结果：从栈底到栈顶依次对S的每个数据元素调用函数visit()，一旦visit()失败，则操作失效 }ADT Stack 队列的抽象数据类型定义： ADT Queue{ 数据对象：D={ai|ai∈ElemSet,i=1,2,…,n,n≥0} 数据关系：Rl={<ai-1,ai>|ai-1,ai∈D,i=2,…,n} 约定其中ai端为队列头，an端为队列尾。 基本操作： InitQueue(&Q) 操作结果：构造一个空队列Q DestroyQueue(&Q) 初始条件：队列Q已存在 操作结果：队列Q被销毁，不再存在 QueueEmpty(Q) 初始条件：队列Q已存在 操作结果：若Q为空队列，则返回TRUE，否则FALSE …… EnQueue(&Q,e) 初始条件：队列Q已存在 操作结果：插入元素e为Q的新的队尾元素 DeQueue(&Q,&e) 初始条件：Q为非空队列 操作结果：删除Q的队头元素，并用e返回其值 }ADT Queue 2．主程序的流程： 调用CreateDN函数创建图的邻接表G； 调用PrintDN函数输出邻接表G； 调用DFSTraverse函数深度优先遍历图； 调用BFSTraverse函数广度优先遍历图 图的遍历是图论中的基础操作，主要包含深度优先遍历(DFS)和广度优先遍历(BFS)两种算法。这两种算法在处理图结构数据时非常关键，例如在网络爬虫、社交网络分析、最短路径计算等领域都有广泛应用。 深度优先遍历是一种递归的搜索策略，它尽可能深地探索图的分支。在非递归实现中，通常使用栈来辅助完成遍历。DFS的基本步骤如下： 1. 从某个起始顶点开始，将其标记为已访问。 2. 将该顶点的所有未访问过的邻接点压入栈中。 3. 如果栈不为空，弹出栈顶顶点，重复步骤2。 4. 当所有顶点都被访问过，遍历结束。 广度优先遍历是一种层次遍历，先访问离起点近的顶点，再访问远的顶点。在非递归实现中，通常使用队列来辅助完成遍历。BFS的基本步骤如下： 1. 创建一个队列，将起始顶点放入队列，并标记为已访问。 2. 当队列不为空时，取出队首顶点，访问它，然后将它的所有未访问过的邻接点加入队列。 3. 重复步骤2，直到队列为空，遍历结束。 在上述系统设计中，定义了图的抽象数据类型ADT Graph，包括顶点集V、弧集VR和一系列操作如创建、销毁、添加顶点和弧以及深度优先和广度优先遍历。此外，还定义了栈和队列的抽象数据类型，它们是实现图遍历的关键数据结构。 对于给定的需求分析，要输出从顶点0开始的DFS和BFS序列，可以按照以下步骤进行： 1. 初始化图G，可以使用邻接矩阵或邻接表来存储图的结构。 2. 对于DFS，从顶点0开始，将访问过的顶点标记并压入栈中，然后处理其邻接点，直至遍历完整个图。 3. 对于BFS，同样从顶点0开始，将其加入队列，然后逐个处理队列中的顶点及其未访问过的邻接点，直至队列为空。 在实现这些操作时，FirstAdjVex和NextAdjVex函数用于获取顶点u的第一个和下一个邻接顶点。在非递归BFS中，FirstAdjVex应返回顶点u的第一个邻接顶点，而NextAdjVex则用于在遍历邻接顶点时找到下一个未访问的邻接顶点。 主程序流程包括创建图、打印图、进行深度优先遍历和广度优先遍历。通过调用相应的函数，如CreateDN创建邻接表，PrintDN打印图，DFSTraverse和BFSTraverse分别执行DFS和BFS。 在调试分析中，需要确保FirstAdjVex和NextAdjVex函数的正确性，以及栈和队列的操作无误，这样才能保证图的遍历按预期进行。同时，对于每个遍历过程，要确保每个顶点只被访问一次，避免无限循环或遗漏。在实际应用中，这些算法可能需要进行优化，比如通过位运算标记已访问顶点，提高效率。