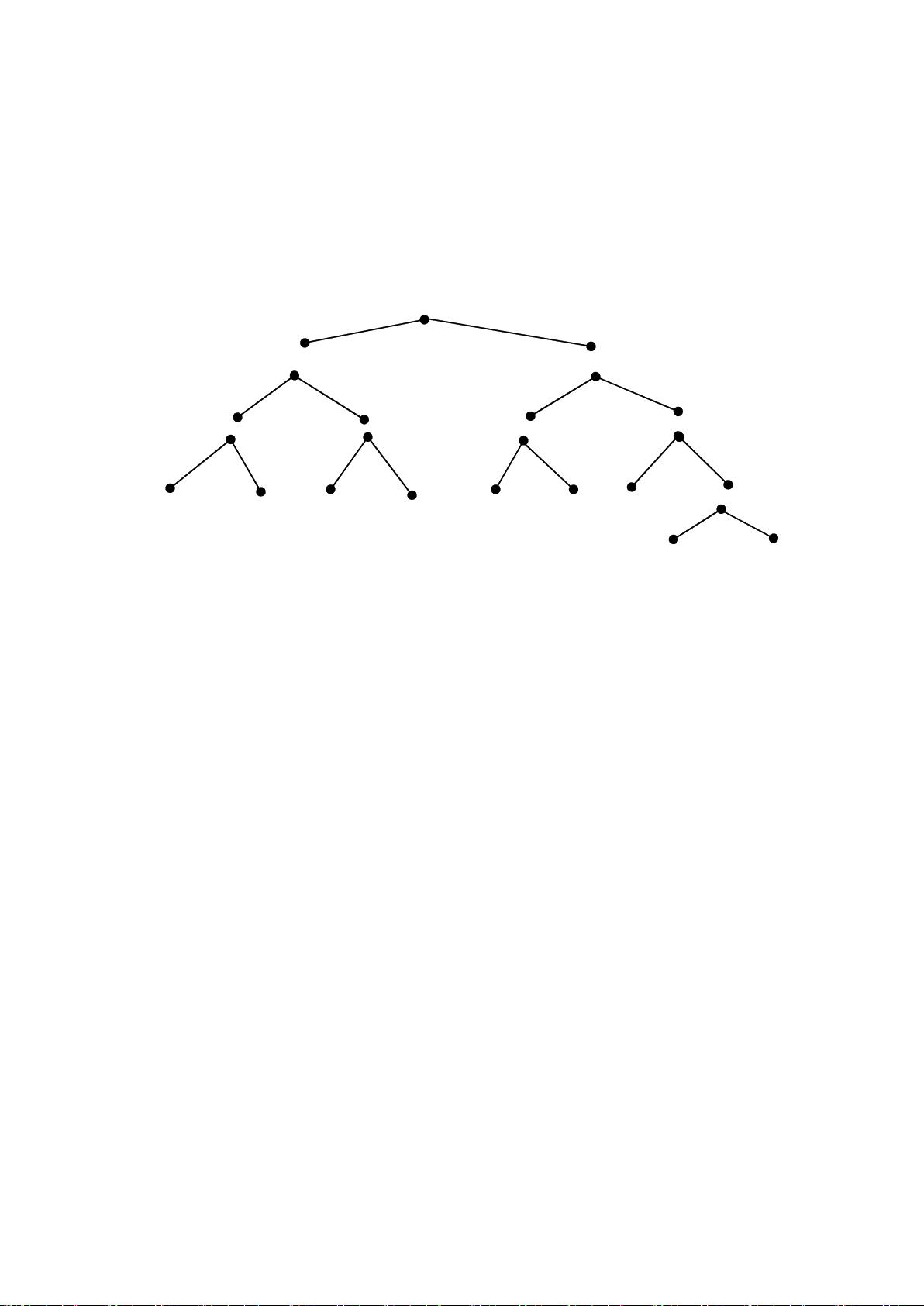
acm 线段树 数据结构

### ACM 线段树 数据结构 #### 一、引言与应用场景 在信息学竞赛中，线段树作为一种高效的数据结构，常被用于解决区间更新与查询的问题。这类问题的特点在于需要对数轴上的一段区间或者数列中连续的若干个数进行统一的操作，例如增加一个值、修改区间内所有数的值、查询区间内的最大值、最小值或求和等。 #### 二、为什么选择线段树？ **例1：** 假设有一列初始值全为0的数，需要支持以下三种操作： 1. 给定区间内的每个数加某个特定值。 2. 将指定区间内的所有数置为同一值。 3. 查询指定区间上的最小值、最大值、所有数的和。 **问题分析：** - **朴素解法**：使用线性表来存储整个数列，并对每一次操作或查询逐个元素进行处理。假设数列长度为 _n_，总操作数为 _m_，则时间复杂度为 O(_mn_)。这种方法在 _n_ 和 _m_ 较大时效率低下。 - **优化思路**：关键在于将针对单个元素的操作转变为区间操作。通过设计一种能直接维护所需处理区间的数据结构，可以显著提高效率。 #### 三、线段树的结构 **定义与特性：** 1. **元线段**：长度为1的线段。 2. **线段树**：一种二叉树，每个节点对应一个区间 [a, b]。叶子节点代表元线段，内部节点的左子树代表区间 [a, (a + b) / 2]，右子树代表区间 [(a + b) / 2, b]。 3. **递归结构**：线段树的结构是递归定义的。以 T(1, 10) 为例，其结构如图所示。 **举例说明：** 考虑区间 [1, 10]，对应的线段树如下所示： - 根节点代表区间 [1, 10]。 - 左子树代表区间 [1, 5]。 - 右子树代表区间 [6, 10]。 - 再继续递归分解，直到达到叶子节点，即单个数字。 **优点**：通过将区间拆分成若干个不相交的小区间，线段树可以有效地处理区间操作。这种结构使得查询和更新操作可以在对数时间内完成。 #### 四、线段树的性质 1. **深度限制**：长度范围为 [1, L] 的线段树的深度不超过 log₂(L - 1) + 1。 2. **结点数量**：线段树上的结点个数不超过 2log₂L 个。 3. **区间划分**：线段树能把区间上的任意一条长度为 L 的线段分成不超过 2log₂L 条线段。 #### 五、线段树的存储方式 **链表实现：** ```c++ struct Node { int Left, Right; Node *LeftChild, *RightChild; }; ``` **数组模拟：** ```c++ int Left[], Right[], LeftChild[], RightChild[]; ``` **压缩存储**：线段树除了最后一层外的所有节点都有两个孩子。可以利用这一点来压缩存储空间，减少不必要的空闲空间。 #### 六、线段树的基本操作 **1. 构建线段树** 构建线段树的过程是从根节点到叶子节点递归进行的。对于每个非叶子节点，需要创建左右子节点并递归构建子树。 **2. 区间更新** - **单一值更新**：将某个指定位置的值更改为新值。 - **区间更新**：对区间内的每个值进行某种操作（如加值或赋值）。 **3. 区间查询** - **查询区间内的最大值/最小值/和**：根据题目需求，通过遍历线段树，合并路径上的值来计算结果。 #### 七、线段树与其它数据结构的对比 - **RMQ（Range Minimum Query）**：仅适用于查询区间最小值，而线段树支持多种操作。 - **树状数组**：适用于单点更新区间查询，但不支持区间更新。 - **平衡树**：支持动态插入删除，但实现复杂度较高。 线段树是一种强大的数据结构，特别适合处理区间操作问题。通过对区间进行递归分割，可以有效地将复杂问题简化为更简单的子问题，从而提高算法的整体效率。