
2 XAMPLING—PART I: PRACTICE
coset sampling [7], the Nyquist-folding ADC [8], the random
demodulator [9] and its parallel version [10], and the mod-
ulated wideband converter [11], [12]. The approaches differ
in the signal model they assume, in the sampling strategy and
in the recovery algorithms. Research on sub-Nyquist sampling
has so far focused on perfect recovery of the Nyquist-rate input
signal. The ability to process the information at baseband,
namely without involving Nyquist-rate computations, was not
addressed. In fact, as shown in this paper, none of the systems
proposed in [2]–[12] allow for baseband DSP, including the
previous works [7], [11] by the authors. Admittedly, whenever
x(t) can be recovered, DSP at the high Nyquist rate is possible.
However, this solution wastes the DSP resources and typically
results in impractical processing rates.
The main contribution of this two-part series is a design
methodology for sub-Nyquist systems, named Xampling. The
nomenclature we chose will be explained below. Part one, the
present paper, begins with the practical aspects of the Xam-
pling methodology. The framework consists of four criteria:
broad signal model, low sampling rate, efficient analog and
digital implementation and the baseband processing capability.
Our previous publications on multiband sampling incorporated
the model and the rate considerations [7], [13], whereas [11]
added the aspect of practical implementation. The Xampling
methodology has matured from these works and [12]. The
present paper capitalizes on the necessity of baseband process-
ing and on the digital input type that standard DSP packages
are designed to deal with. Section II elaborates more on these
properties, which we consider as ground rules for a successful
sub-Nyquist solution. In the same section, we address the
relation to compressed sensing (CS), an active research field
that was triggered by the works of [14], [15]. Mainstream CS
works study the problem of recovering a sparse vector from
an underdetermined linear system. In contrast, Xampling is a
broad framework for treating analog signals, which takes into
account considerations that are not treated in discrete CS.
Part two of Xampling [16] capitalizes on the difference be-
tween classic sampling theory and sub-Nyquist from a deeper
theoretical perspective. The former relies on a single subspace
model [17], whereas analog sparsity, such as multiband with
unknown carriers, fits the model of a union of subspaces
[12], [18]–[22]. Continuing the pragmatic theme of the present
paper, part two introduces additional Xampling criteria for the
theoretical study of rate and stability of sub-Nyquist systems.
The first part of the present paper is devoted to support the
proposed methodology and its design rules. We revisit [7]–[12]
in light of the four Xampling criteria. Our survey is inspective
rather than descriptive – each strategy is briefly overviewed,
after which we study various practical considerations, which
did not appear in the original publications. We begin with
pointwise strategies which are shown to suffer from practical
analog bandwidth limitations of existing hardware devices.
These limitations hold regardless of whether knowledge of
the carrier positions is available [2]–[6] or absent [7], and
become acute for wideband signals. The Nyquist-folding sys-
tem [8] also involves possible pointwise limitations. We then
proceed to examine in detail two state-of-the-art systems:
the random demodulator (RD) [9], [10] and the modulated
wideband converter (MWC), proposed by the authors in [11].
Our analysis relies on the viewpoint of equivalent systems,
explained in Section IV. The comparison reveals that the RD
relies on a sensitive signal model when dealing with analog
signals, the time-domain approach boils down to difficult im-
plementation requirements and the computational complexity
is severe, as discussed in detail in Section IV. In contrast, the
MWC naturally fits analog models, the implementation [23]
is based on the standard frequency-domain viewpoint and the
required computational complexity is by orders of magnitude
smaller compared with the RD. Unfortunately, we conclude
that all the methods we survey, including the MWC, do not
support baseband processing. Therefore, the impact of [2]–[12]
reduces to digital storage of the samples and reconstruction of
the input x(t). The prominent advantage of DSP at baseband,
which is the prime reason for shifting to digital, is not achieved
by these systems.
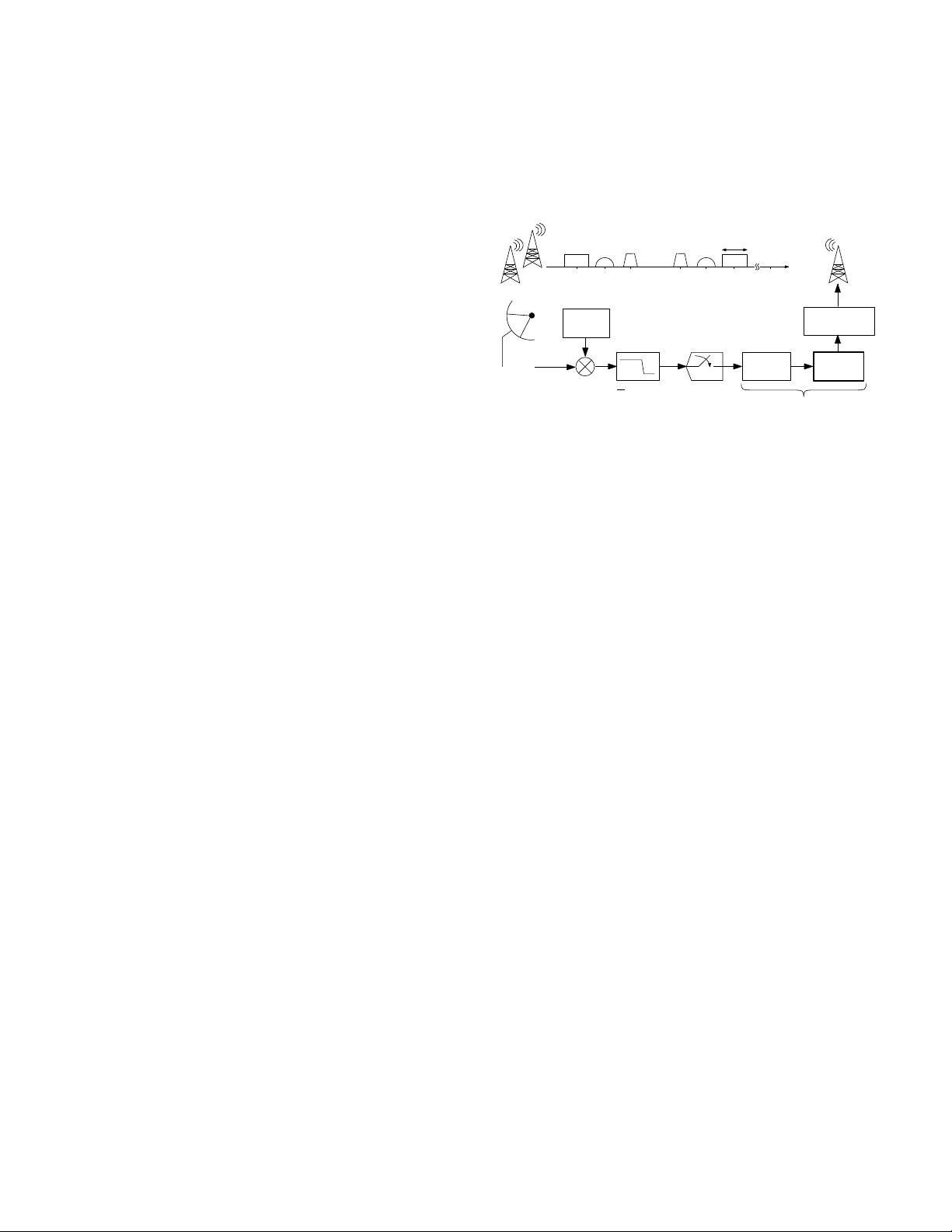
Our second contribution is a digital algorithm that translates
the MWC outputs to the required format for baseband pro-
cessing. We choose to treat the MWC system since it satisfies
all the other criteria of Xampling. Two ingredients that are
computed by [11] are prerequisites: a coarse estimate of the
spectral support and a set of lowrate sequences that together
capture the signal information. The algorithm consists of three
stages: refining the frequency support estimate, isolating the
transmissions, and finally a digital carrier recovery stage. The
last step utilizes the balanced quadricorrelator, a reliable fre-
quency detector which is suitable for many data transmission
techniques [24]. As a nice feature, we show that once the
algorithm is applied and the information is extracted from the
samples, the input x(t) can be reconstructed more efficiently
than the method proposed in [11]. Numerical simulations
demonstrate the algorithm accuracy in typical noisy wideband
scenarios. The consequence is that any existing DSP algorithm
of interest can smoothly interface with the MWC.
The third and final contribution of the paper applies the
MWC to spectrum sensing, one of the fundamental tasks
in cognitive radio systems [25]. The cognitive receiver uses
spectrum sensing to decide on available spectrum regions that
may be useful for transmissions, until the licensed owner
of those bands appear. We present two configurations of the
MWC for spectrum sensing which rely on the implementation
advantages of the MWC in the wideband regime, and on
our digital algorithm. Related works in the field [10], [26]–
[30] are discussed and compared within the unified Xampling
framework.
The paper is organized as follows. Section II introduces
the Xampling methodology, addresses the relation to CS and
explains the nomenclature. The three following sections are
dedicated to examine the validity of the methodology: lowrate
pointwise sampling in Section III; the RD in Section IV;
and the MWC in Section V. A mid-term summary is given
in Section VI. The digital algorithm that enables baseband
processing with the MWC is provided and simulated in
Section VII. Finally, in Section VIII, we explain how to apply
the MWC and the proposed algorithm to efficient spectrum
sensing in sub-Nyquist cognitive radio receivers.



 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功