用MATLAB实现模拟退火算法PPT学习教案.pptx

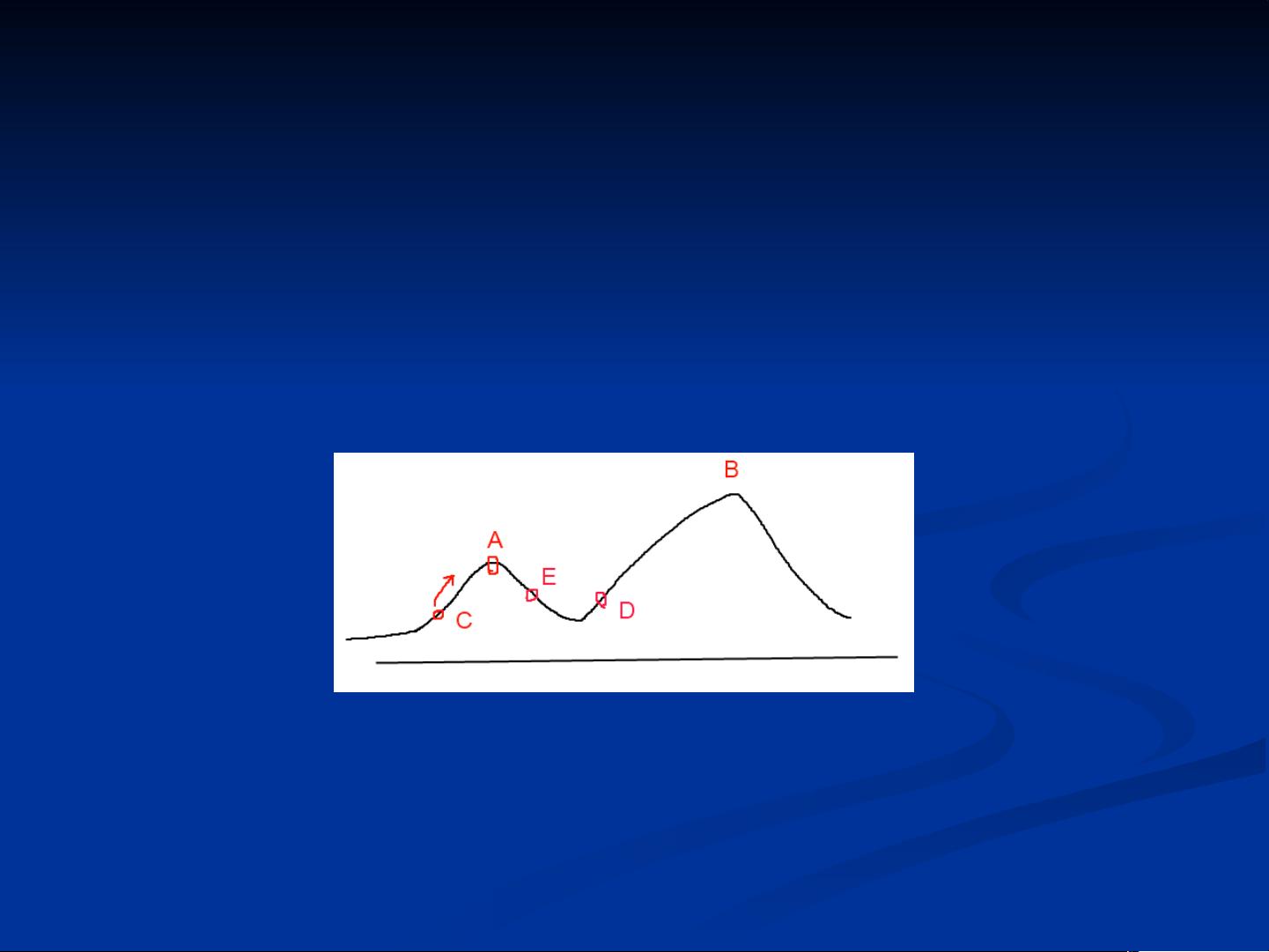
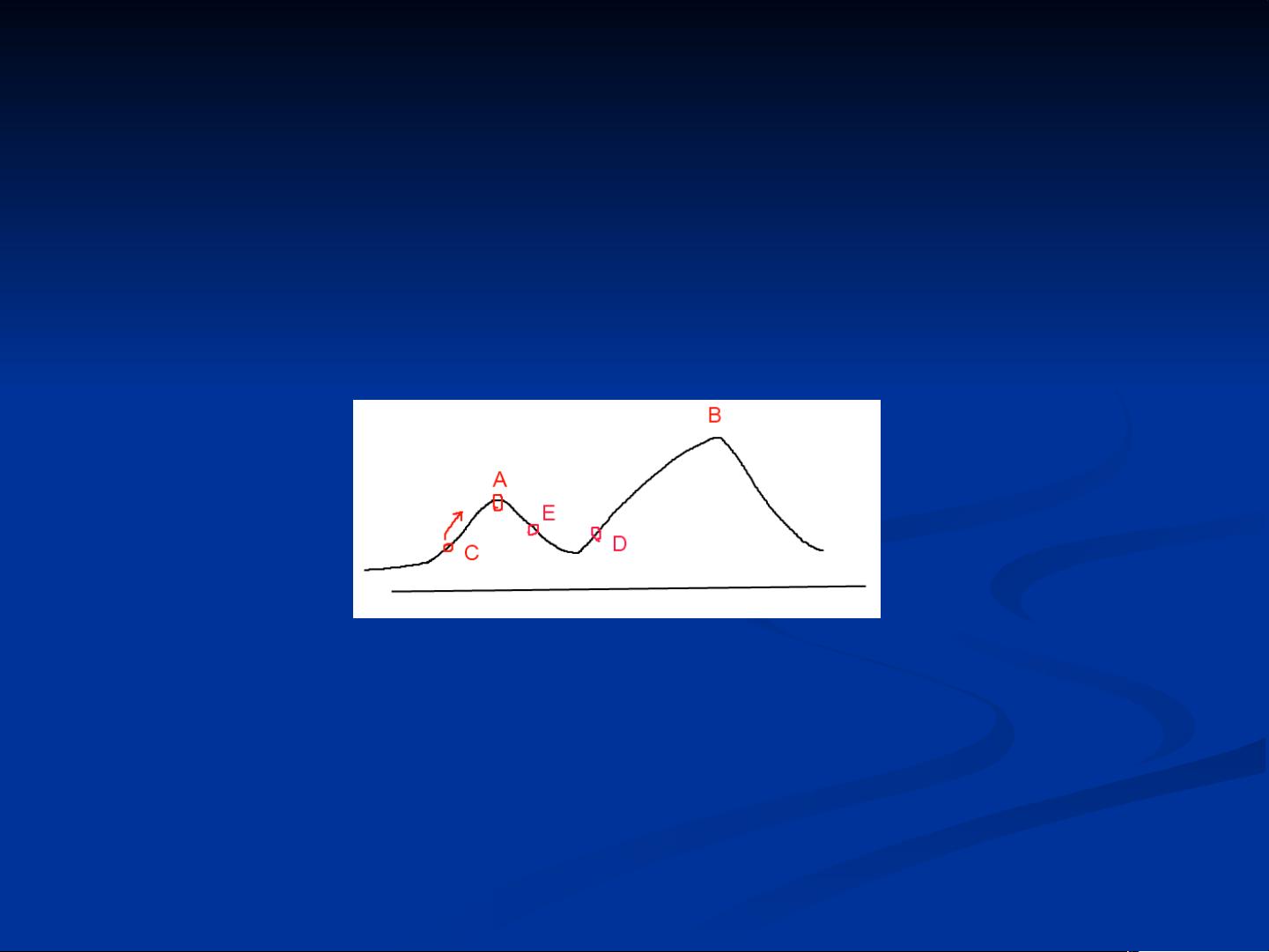
《用MATLAB实现模拟退火算法》PPT学习教案详细解析 模拟退火算法是一种基于物理退火原理的全局优化算法，广泛应用于解决复杂的非线性优化问题。它结合了贪心策略和随机性，避免了传统算法陷入局部最优的困境。在MATLAB中实现模拟退火算法，可以帮助我们更好地理解和应用这一强大的工具。 1. **算法基本理论** - **退火过程**：受固体退火过程启发，模拟退火算法通过改变“温度”参数T，模拟物质从高温到低温的冷却过程。在高温阶段，算法允许接受较优或较劣的解，以便探索更广阔的解空间；随着温度降低，算法更倾向于接受最优解，从而逐渐接近全局最优。 - **Metropolis准则**：新解被接受的概率P取决于新旧解的差异以及当前温度T。当新解质量更好时，新解总是被接受；当新解质量更差时，新解仍有概率被接受，且概率随T的降低而减小。 2. **算法基本步骤** - **初始化**：设定初始温度和随机产生初始解。 - **扰动与接受**：在每个温度阶段，生成新的解，计算目标函数变化，并根据Metropolis准则决定是否接受新解。 - **温度调度**：温度按照预定策略逐渐降低，如指数衰减。 - **记录历史最优解**：在整个过程中，记录下迄今为止的最优解，以防在低温阶段错过全局最优。 3. **关键参数** - **初始温度**：需足够高，确保算法在早期阶段能探索整个解空间。 - **终止温度**：设置一个足够低的阈值，使得在该温度下，算法几乎只接受目标函数值不增的解。 - **热平衡时间**：在每个温度阶段，应有足够的迭代次数，以确保系统达到热平衡状态。 4. **新解生成**： - 为了充分探索解空间，新解的生成方法应当多样化，可以是随机扰动、邻域搜索或其他启发式策略。 5. **收敛条件**： - 初始温度足够高，保证能跳出局部最优。 - 热平衡时间足够长，确保在每个温度下系统有充分时间达到稳定。 - 终止温度足够低，以捕获全局最优解。 MATLAB作为一种强大的数值计算平台，提供了丰富的数学工具和图形界面，非常适合实现模拟退火算法。通过编写MATLAB代码，用户可以自定义目标函数、温度调度策略以及新解生成方式，灵活适应各种优化问题。此外，MATLAB的可视化功能还能帮助分析算法的运行过程和结果，加深对模拟退火算法的理解。 用MATLAB实现模拟退火算法的学习教案，旨在教授如何利用编程技术解决复杂优化问题，同时也强调了算法背后的理论基础和实际应用。通过实践，学习者不仅可以掌握一种强大的优化工具，还能培养解决实际问题的能力。