支持向量机通俗导论

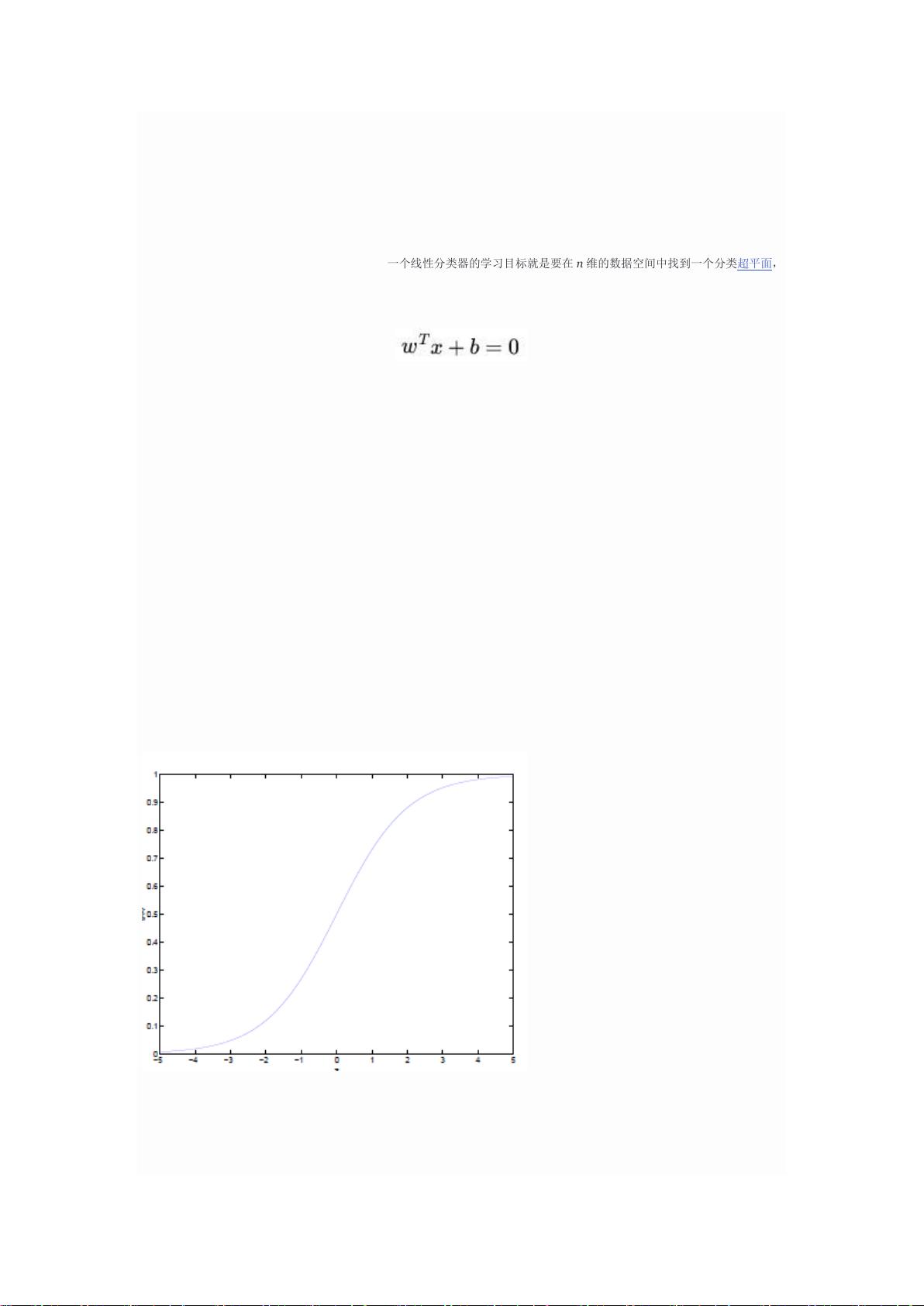
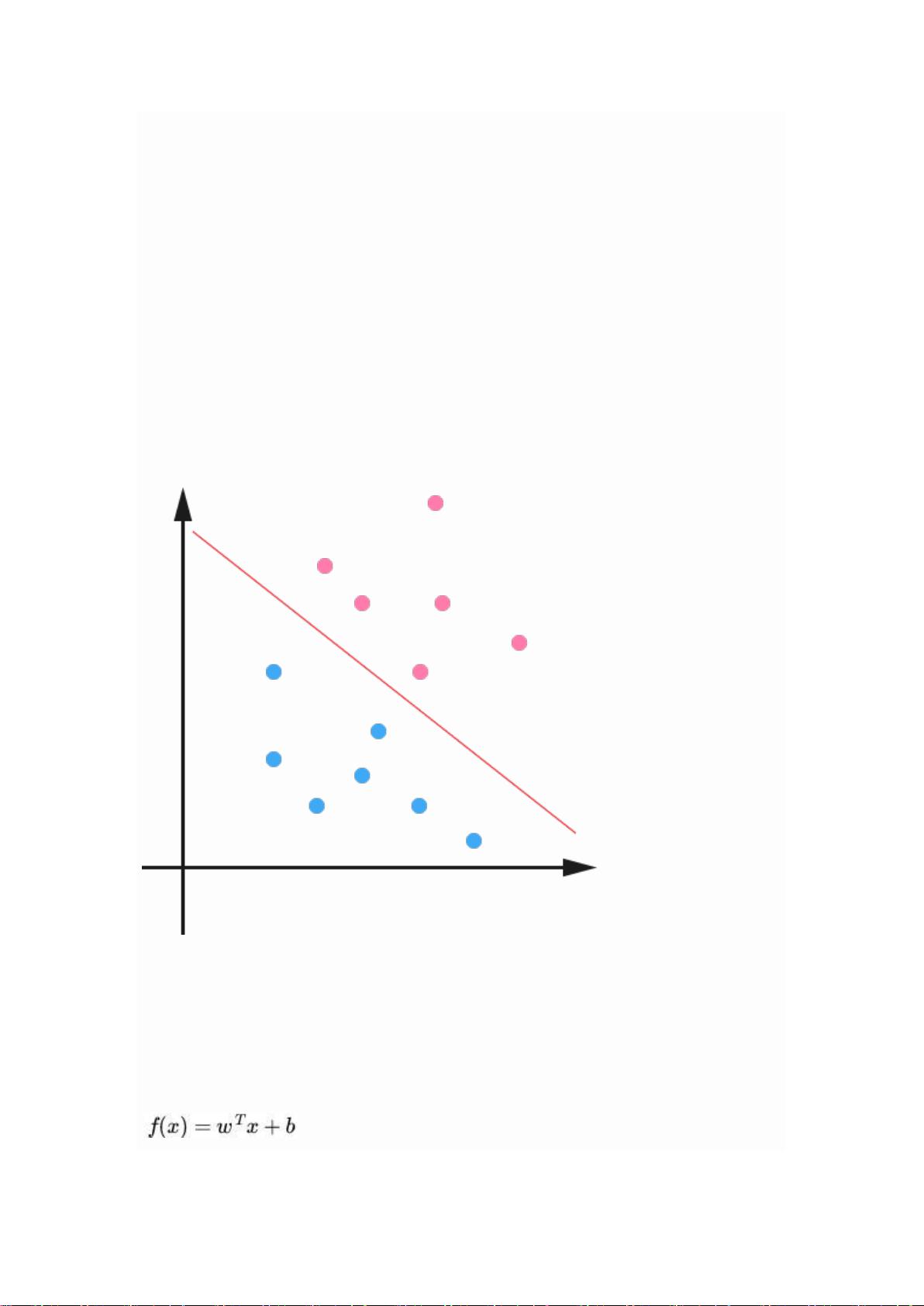
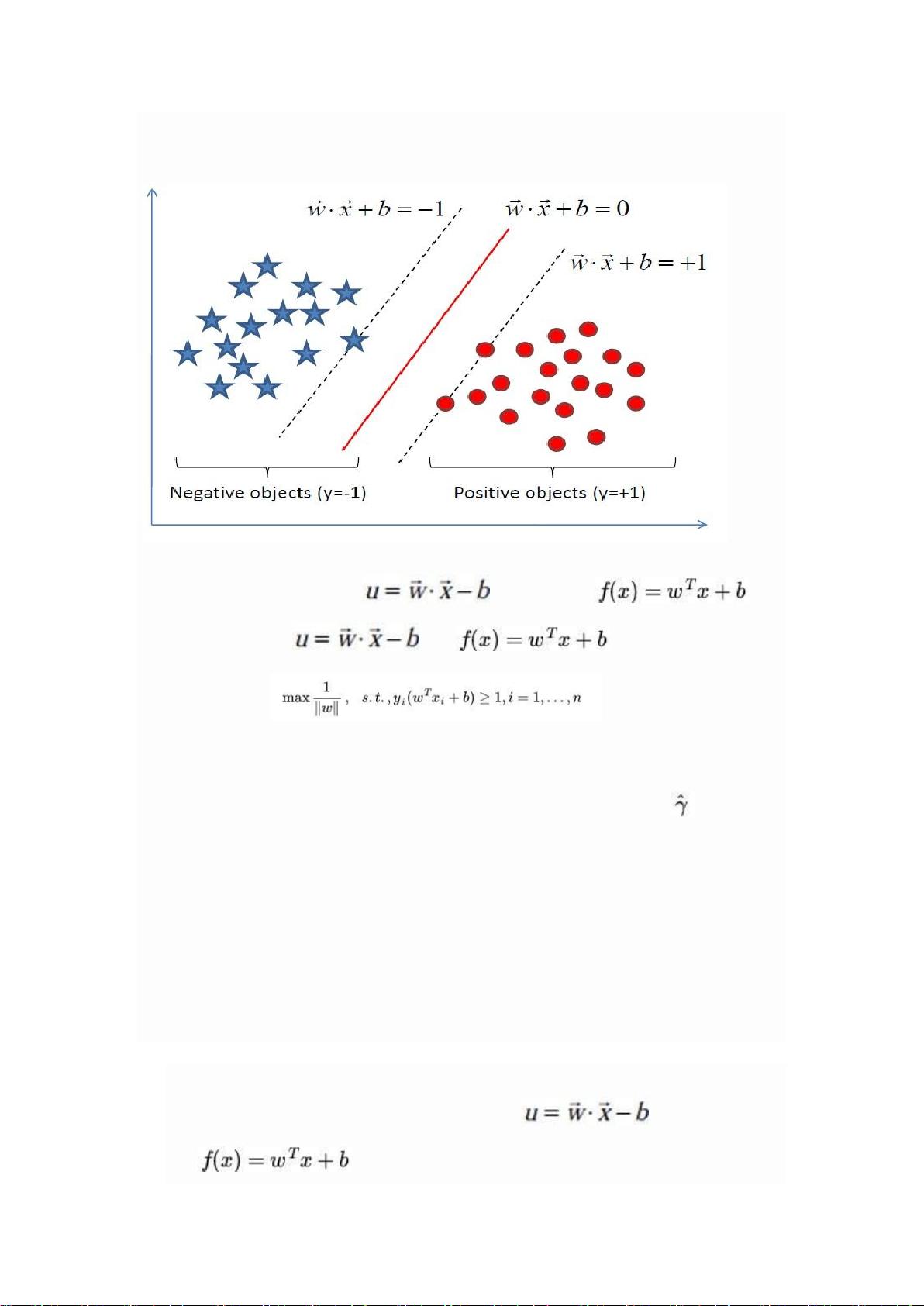
### 支持向量机(SVM)通俗导论 #### 1.0 什么是支持向量机SVM **支持向量机**(Support Vector Machine, SVM)是一种在数据挖掘领域非常重要的分类技术，用于构建分类模型。SVM的核心思想是在特征空间中寻找一个决策边界（也称为超平面），该边界能够最大程度地区分不同类别的样本点。SVM的目标不仅在于准确分类训练数据集，更在于提高模型的泛化能力，使其能够在未知数据上表现良好。 #### 1.1 线性分类 **1.1.1 分类标准** 在讨论支持向量机之前，我们首先需要了解“线性分类器”这一概念。在线性分类问题中，我们考虑的是将输入数据（通常表示为多维向量）分为两类的问题。例如，假设我们有一个二维空间中的数据集，每个样本点由一个二维向量\(x = (x_1, x_2)\)表示，目标是根据这些样本点划分两个不同的类别。类别用\(y\)表示，可以取值为1或-1，分别代表两个不同的类。 **1.1.2 1或-1分类标准的起源：Logistic回归** 为什么选择1或-1作为类别标记？这起源于Logistic回归。Logistic回归是一种用于预测因变量为二元分类结果的统计方法。它利用Logistic函数（也称Sigmoid函数）将线性组合的预测值映射到(0,1)之间，作为属于某一类的概率估计。具体而言，假设我们有特征向量\(x\)，预测概率为： \[ P(y=1|x) = \sigma(w^Tx + b) \] 其中，\(\sigma(z) = \frac{1}{1 + e^{-z}}\) 是Logistic函数，\(w\)是权重向量，\(b\)是偏置项。如果\(\sigma(w^Tx + b) > 0.5\)，则预测类别为1；否则预测类别为0。这种设定使得分类更加直观且易于处理。 **1.1.3 形式化表示** 对于分类标准，我们通常用\(y = \pm 1\)来表示，这不仅符合Logistic回归中的预测逻辑，也有助于简化后续的数学推导。例如，在SVM中，决策边界（超平面）的方程通常被表示为： \[ w^Tx + b = 0 \] 其中，\(w\)是权向量，\(b\)是偏置项。对于给定的样本点\(x\)，若\(w^Tx + b > 0\)，则该点属于类别1；若\(w^Tx + b < 0\)，则属于类别-1。 #### 1.2 线性分类的一个例子 考虑一个二维平面中的简单例子，假设我们有一组数据点，分为红色和蓝色两组，如图所示。目标是找到一条直线（在二维空间中的超平面），这条直线能尽可能好地将红色点与蓝色点分开。SVM试图找到这样一个超平面，它不仅能够正确分类现有数据，而且还能够最大化不同类别之间的边际距离，从而提高模型的鲁棒性和泛化能力。 ### 第二层：深入了解SVM的数学基础 **2.1 几何间隔与函数间隔** - **几何间隔**：是指样本点到超平面的距离，具体来说，对于一个样本点\(x_i\)，其到超平面\(w^Tx + b = 0\)的几何间隔定义为\(\gamma_i = \frac{|w^Tx_i + b|}{||w||}\)。 - **函数间隔**：对于一个分类为正或负的样本点\(x_i\)，其到超平面\(w^Tx + b = 0\)的函数间隔定义为\(y_i(w^Tx_i + b)\)。 **2.2 最大间隔原则** SVM的核心思想之一是最小化经验风险与结构风险，以获得良好的泛化性能。最大间隔原则即寻找使所有训练样本点的最小几何间隔最大的超平面。这相当于解决一个优化问题： \[ \max_{w,b} \min_i \gamma_i \] 其中，约束条件是所有样本点都要正确分类，即对于每一个训练样本\((x_i, y_i)\)，有\(y_i(w^Tx_i + b) \geq 1\)。 **2.3 硬间隔与软间隔** - **硬间隔**：在完全线性可分的情况下，可以通过最大化间隔来构建分类器，此时所有的训练样本都需要满足\(y_i(w^Tx_i + b) \geq 1\)的约束。 - **软间隔**：在实际应用中，数据往往不是完全线性可分的。为了处理这种情况，SVM引入了松弛变量\(\xi_i\)，允许某些样本点违反约束条件。通过调整惩罚系数\(C\)，可以在间隔最大化与错误分类样本之间进行平衡。 ### 第三层：SVM的高级概念与扩展 **3.1 核技巧** 对于非线性可分的问题，直接在原始特征空间中寻找线性超平面可能会遇到困难。核技巧通过将原始数据映射到更高维度的空间来解决这个问题。常用的核函数包括多项式核、高斯径向基(RBF)核等。 **3.2 多类分类** 虽然SVM本质上是一种二类分类器，但通过使用一对多（one-vs-all）、一对一（one-vs-one）等策略，可以将其应用于多类分类问题。 **3.3 软件工具与库** 实现SVM算法有许多成熟的软件工具和库，如LibSVM、Scikit-Learn等。这些工具提供了高效且易于使用的API，使得SVM可以方便地应用于各种实际问题中。 ### 结语 通过对支持向量机的理解逐步深入，我们可以看到SVM不仅是一种强大的分类方法，而且其背后的数学原理也为其他机器学习算法提供了宝贵的启示。从线性分类的基础到最大间隔原则，再到核技巧和多类分类的应用，SVM提供了一个全面而深入的框架，帮助我们更好地理解复杂数据背后的模式和规律。