python1All Algorithms implemented in PythonPGJ.zip

# Binary Tree Traversal ## Overview The combination of binary trees being data structures and traversal being an algorithm relates to classic problems, either directly or indirectly. > If you can grasp the traversal of binary trees, the traversal of other complicated trees will be easy for you. The following are some common ways to traverse trees. - Depth First Traversals (DFS): In-order, Pre-order, Post-order - Level Order Traversal or Breadth First or Traversal (BFS) There are applications for both DFS and BFS. Stack can be used to simplify the process of DFS traversal. Besides, since tree is a recursive data structure, recursion and stack are two key points for DFS. 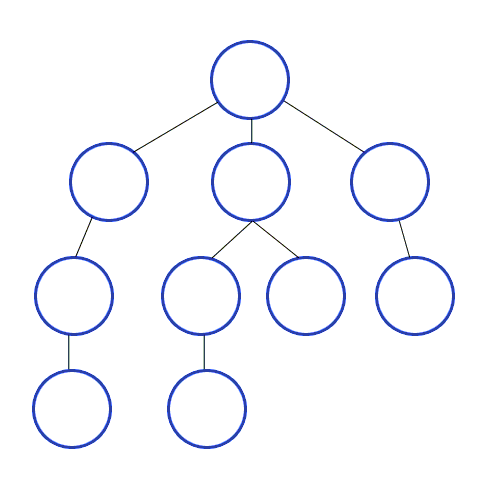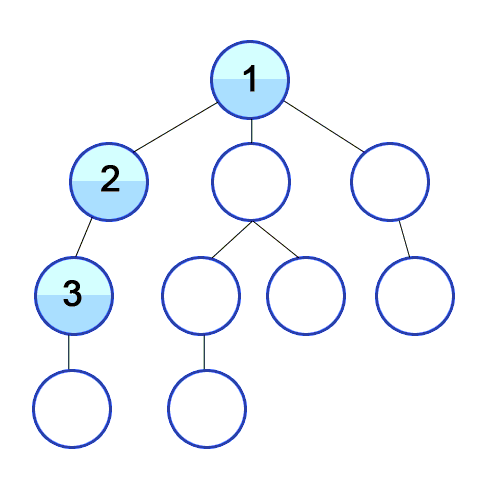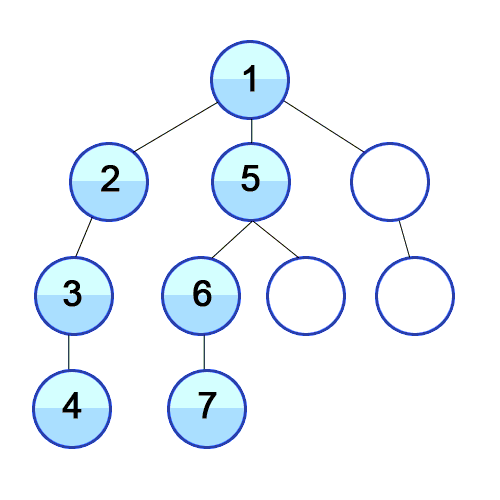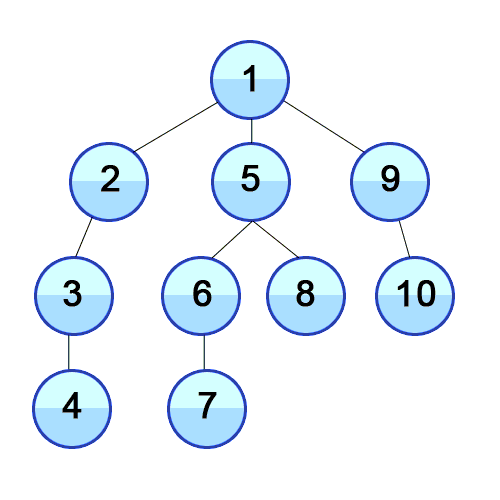Graph for DFS:  The key point of BFS is how to determine whether the traversal of each level has been completed. The answer is to use a variable as a flag to represent the end of the traversal of current level. ## Pre-order Traversal The traversal order of pre-order traversal is `root-left-right`. Algorithm Pre-order 1. Visit the root node and push it into a stack. 2. Pop a node from the stack, and push its right and left child node into the stack respectively. 3. Repeat step 2. Conclusion: This problem involves the classic recursive data structure (i.e. a binary tree), and the algorithm above demonstrates how a simplified solution can be reached by using a stack. If you look at the bigger picture, you'll find that the process of traversal is as followed. `Visit the left subtrees respectively from top to bottom, and visit the right subtrees respectively from bottom to top`. If we are to implement it from this perspective, things will be somewhat different. For the `top to bottom` part we can simply use recursion, and for the `bottom to top` part we can turn to stack. ## In-order Traversal The traversal order of in-order traversal is `left-root-right`. So the root node is not printed first. Things are getting a bit complicated here. Algorithm In-order 1. Visit the root and push it into a stack. 2. If there is a left child node, push it into the stack. Repeat this process until a leaf node reached. > At this point the root node and all the left nodes are in the stack. 3. Start popping nodes from the stack. If a node has a right child node, push the child node into the stack. Repeat step 2. It's worth pointing out that the in-order traversal of a binary search tree (BST) is a sorted array, which is helpful for coming up simplified solutions for some problems. ## Post-order Traversal The traversal order of post-order traversal is `left-right-root`. This one is a bit of a challenge. It deserves the `hard` tag of LeetCode. In this case, the root node is printed not as the first but the last one. A cunning way to do it is to: Record whether the current node has been visited. If 1) it's a leaf node or 2) both its left and right subtrees have been traversed, then it can be popped from the stack. As for `1) it's a leaf node`, you can easily tell whether a node is a leaf if both its left and right are `null`. As for `2) both its left and right subtrees have been traversed`, we only need a variable to record whether a node has been visited or not. In the worst case, we need to record the status for every single node and the space complexity is `O(n)`. But if you come to think about it, as we are using a stack and start printing the result from the leaf nodes, it makes sense that we only record the status for the current node popping from the stack, reducing the space complexity to `O(1)`. ## Level Order Traversal The key point of level order traversal is how do we know whether the traversal of each level is done. The answer is that we use a variable as a flag representing the end of the traversal of the current level.  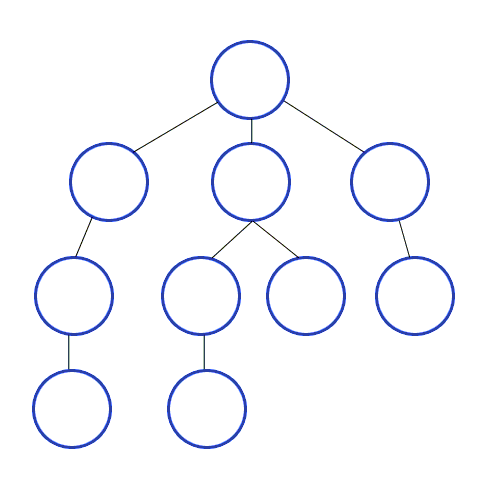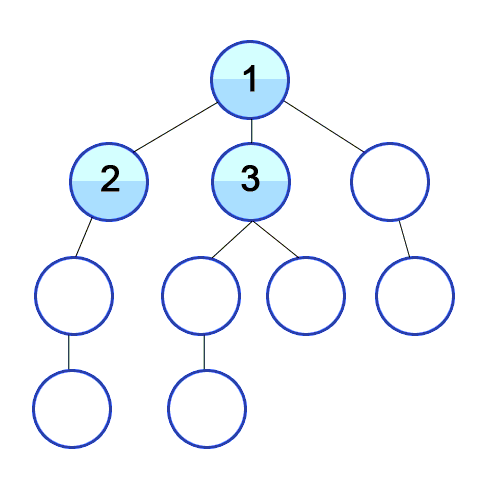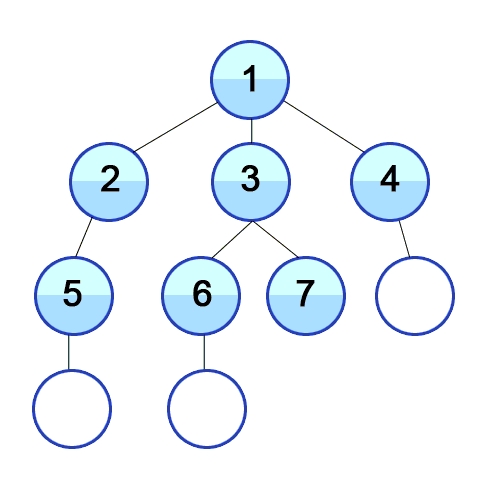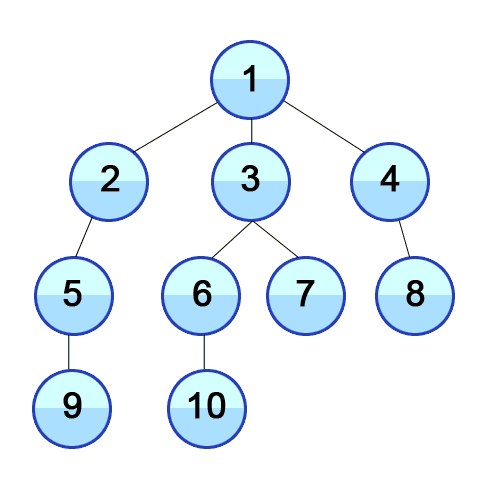Algorithm Level-order 1. Visit the root node, put it in a FIFO queue, put in the queue a special flag (we are using `null` here). 2. Dequeue a node. 3. If the node equals `null`, it means that all nodes of the current level have been visited. If the queue is empty, we do nothing. Or else we put in another `null`. 4. If the node is not `null`, meaning the traversal of current level has not finished yet, we enqueue its left subtree and right subtree respectively. ## Bi-color marking We know that there is a tri-color marking in garbage collection algorithm, which works as described below. - The white color represents "not visited". - The gray color represents "not all child nodes visited". - The black color represents "all child nodes visited". Enlightened by tri-color marking, a bi-color marking method can be invented to solve all three traversal problems with one solution. The core idea is as follow. - Use a color to mark whether a node has been visited or not. Nodes yet to be visited are marked as white and visited nodes are marked as gray. - If we are visiting a white node, turn it into gray, and push its right child node, itself, and it's left child node into the stack respectively. - If we are visiting a gray node, print it. Implementation of pre-order and post-order traversal algorithms can be easily done by changing the order of pushing the child nodes into the stack. Reference: [LeetCode](https://github.com/azl397985856/leetcode/blob/master/thinkings/binary-tree-traversal.en.md)