动态规划技术

动态规划技术是一种优化方法，由美国数学家R.E.Bellman在1951年提出，主要用于解决多阶段决策过程中的最优化问题。它通过将复杂问题分解为一系列子问题，然后逐一解决这些子问题，最终组合成全局最优解。动态规划的核心思想是将多阶段决策转化为单阶段问题，通过最优化原理来寻找最佳策略。 动态规划问题的特点是问题的状态会随着决策的进行而变化。在每个阶段，系统处于特定状态，可以选择一个决策转移到下一个状态，并获得相应的效益。决策序列构成策略，目标是找到一个策略，使得所有阶段的效益之和最大化或最小化（根据问题的具体目标）。 多阶段决策问题的要素包括： 1) 阶段：将整个过程划分为多个阶段，每个阶段有其特定的状态和决策集合。 2) 状态：表示系统在某一时刻的状态，可以是数值、向量或集合等。 3) 决策：每个阶段可以选择的行动，决策会影响下一个阶段的状态和收益。 4) 效益：每个决策带来的好处，可能是当前阶段的直接收益或对未来阶段的影响。 5) 策略：在整个过程中选择的一系列决策，决定了整个过程的轨迹。 动态规划与静态规划（如线性规划、非线性规划）的区别在于，静态规划通常针对的是不随时间变化的问题，而动态规划则涉及时间序列的决策。尽管如此，静态规划问题可以通过引入时间因素转化为动态规划问题来解决。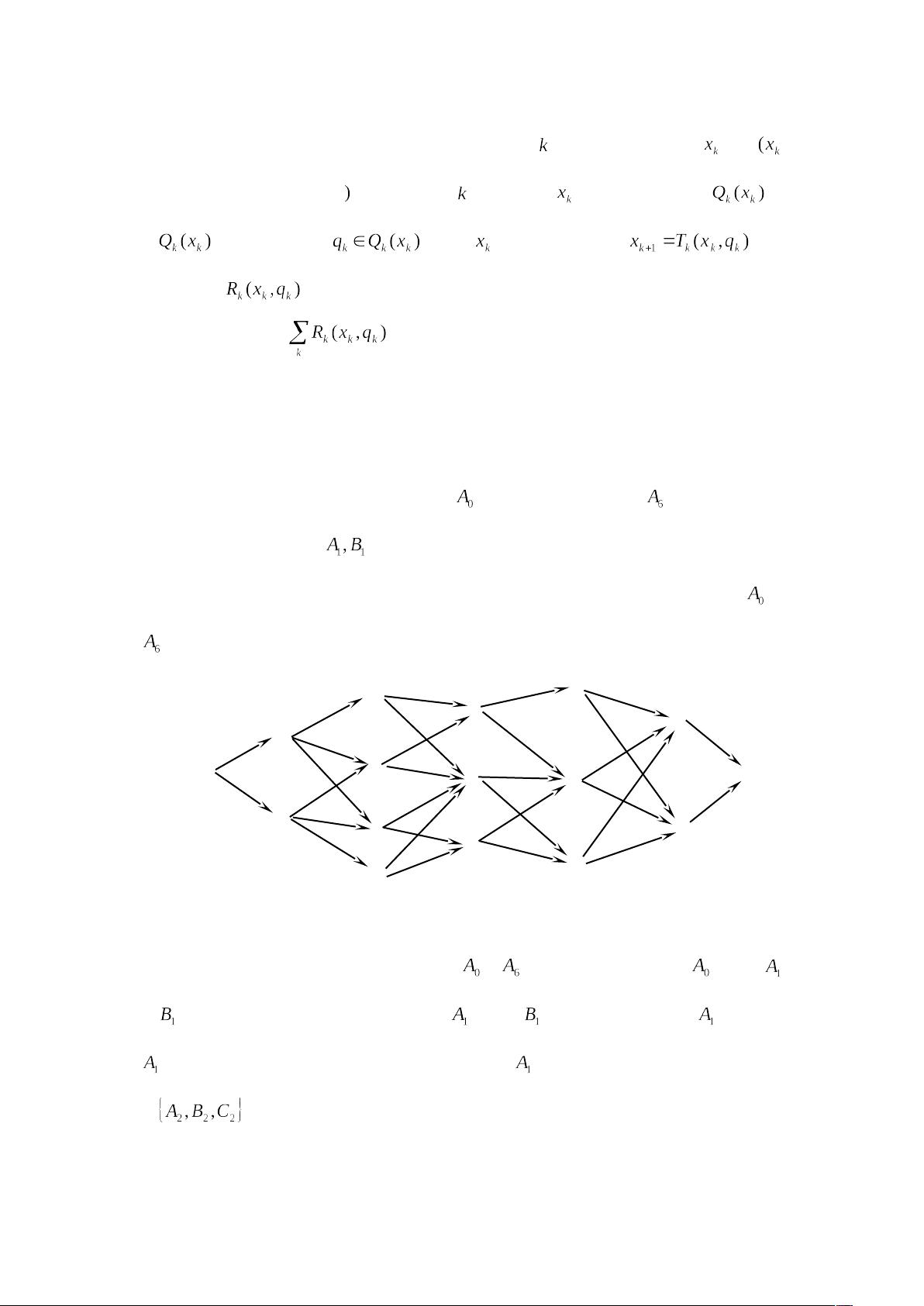 动态规划的应用非常广泛，例如在最短路径问题、库存管理、资源分配、生产调度、设备更新、排序和装载等问题中。例如，图5.1.1所示的煤气管道铺设问题，就是要找到从点A到点B的最短路径，这个问题可以通过动态规划的分阶段决策来解决，每个阶段代表从一个节点到另一个节点的决策。 在实际应用中，动态规划通常需要通过软件工具来求解，如LINGO软件。通过建立适当的模型和方程，可以将问题输入到LINGO中，由软件自动求解出最优策略。 解决动态规划问题的关键步骤包括状态定义、决策规则制定、状态转移方程构建、最优性原则（如Bellman的最优化原理）的运用以及边界条件设定。动态规划模型可能存在多种解法，但最终的目标是找到全局最优解，而不仅仅是局部最优。 动态规划的难点在于理解和构建适当的状态空间，以及正确地定义和应用最优化原理。理解和掌握动态规划的基本概念、原理和方程是学习动态规划的基础，而能够熟练应用LINGO等工具进行求解则是实践中的重要技能。通过深入学习和实践，可以有效解决各种复杂的最优化问题。