非常浅显易懂的傅里叶变换讲解,让你理解为什么要做傅里叶变换
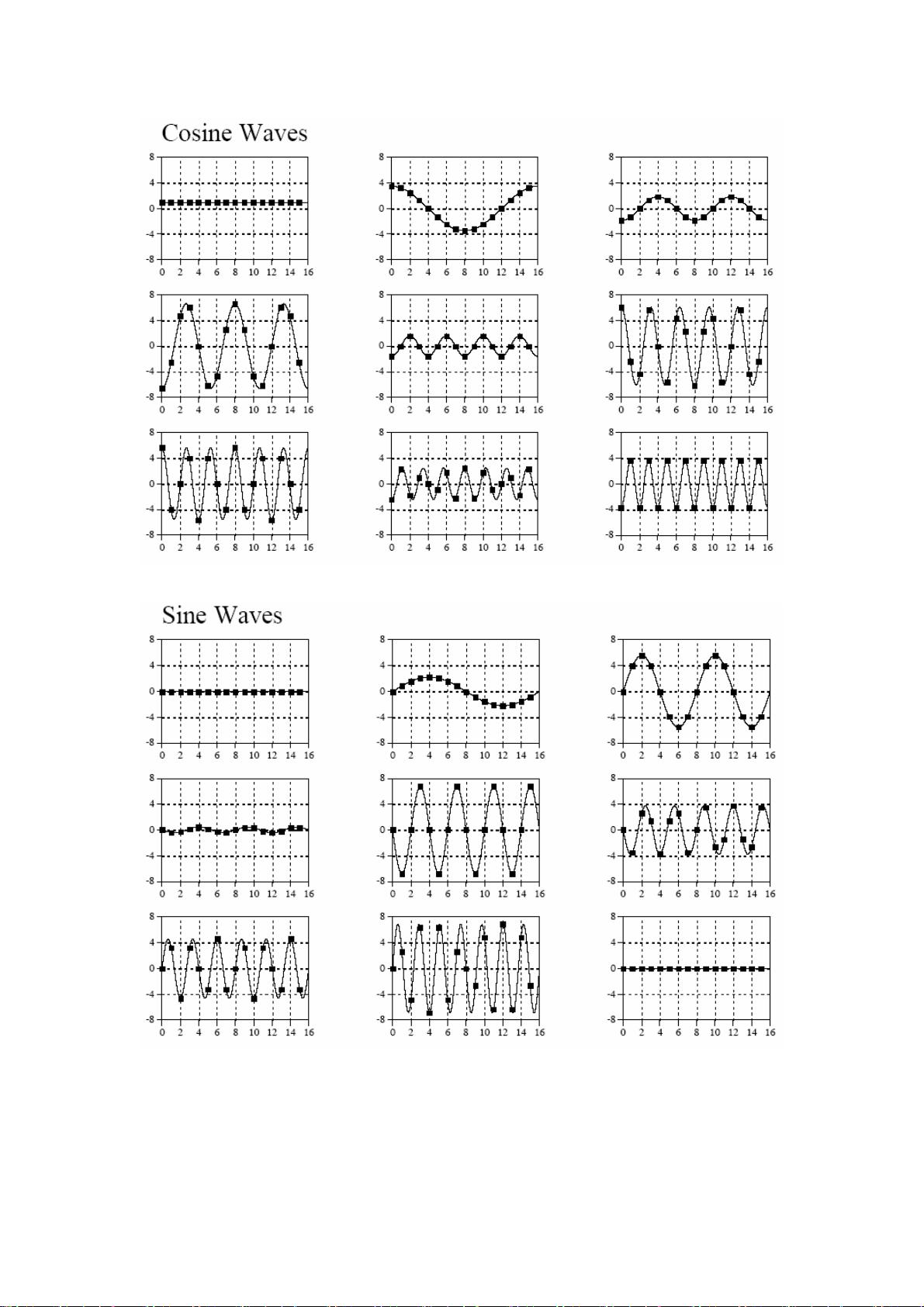
### 傅里叶变换详解 #### 一、傅里叶变换的历史背景与提出 傅里叶变换是一种将时间域内的信号转换为频率域内表示的技术。这一概念最早由法国数学家约瑟夫·傅里叶(Jean-Baptiste Joseph Fourier)在19世纪初提出。傅里叶对热传导问题的研究激发了他的思考,并导致了他在1807年向法国科学院提交的一篇论文。在这篇论文中,傅里叶提出了一个激进的想法:任何连续周期信号都可以通过一组适当选择的正弦曲线的线性组合来表示。尽管这一观点在当时引起了争议,尤其是遭到了著名数学家拉格朗日的反对,但最终傅里叶的理论还是得到了认可。 #### 二、为什么使用正弦曲线? 在探讨傅里叶变换之前,有必要了解为什么傅里叶选择了正弦曲线作为构建信号的基础。正弦曲线具有特殊的性质,即其可以通过线性组合保持信号的形状不变。这意味着如果一个正弦信号经过线性系统,输出仍然保持正弦波形,只是幅度和相位可能会有所改变。这种“保真度”使得正弦曲线成为构建复杂信号的理想选择,因为它们能够简化信号分析过程。 #### 三、傅里叶变换的分类 根据信号的性质,傅里叶变换可以分为以下几类: 1. **非周期性连续信号**:这类信号适用于**傅里叶变换(Fourier Transform, FT)**。 2. **周期性连续信号**:这类信号适用于**傅里叶级数(Fourier Series, FS)**。 3. **非周期性离散信号**:这类信号适用于**离散时域傅里叶变换(Discrete Time Fourier Transform, DTFT)**。 4. **周期性离散信号**:这类信号适用于**离散傅里叶变换(Discrete Fourier Transform, DFT)**。 #### 四、离散傅里叶变换(DFT) 对于实际应用而言,尤其是涉及数字信号处理的领域,最常用的是离散傅里叶变换(DFT)。DFT主要用于处理长度有限的离散信号。在计算机处理中,信号往往是采样后的离散值序列,因此DFT成为一种重要的工具。 - **DFT的重要性**:DFT之所以重要,是因为它提供了一种有效的方法来分析和处理离散信号。它不仅能够揭示信号中的频率成分,还能够用于信号滤波、频谱分析等多种应用场景。 - **DFT的应用**:DFT广泛应用于音频处理、图像处理、通信系统等领域。例如,在音频编码技术中,DFT用于分析声音信号的频谱特征;在图像处理中,它可以用于去除噪声或者进行图像压缩。 #### 五、傅里叶变换的实际意义 理解傅里叶变换的实际意义非常重要,因为它不仅仅是数学上的变换,更是一种强大的工具,可以帮助我们在不同的领域解决问题。通过将信号从时间域转换到频率域,我们可以更好地理解信号的特性,从而设计出更有效的算法和技术。 ### 结论 傅里叶变换作为一种基本的数学工具,在现代科学技术和工程实践中发挥着不可或缺的作用。通过对傅里叶变换的学习,我们可以深入理解信号处理的基本原理,进而利用这些原理解决实际问题。无论是对于学习电气工程的学生还是从事相关工作的专业人士来说,掌握傅里叶变换都是非常重要的。



剩余20页未读,继续阅读

- #完美解决问题
- #运行顺畅
- #内容详尽
- #全网独家
- #注释完整
 ronald6122012-12-02从原理上讲了傅里叶,真的很好
ronald6122012-12-02从原理上讲了傅里叶,真的很好 kenau20102012-02-07这笔记好用!因为之前看过很多傅里叶的书,都不是很懂(本来数学基础不太好) 看这笔记的讲解,基本概念都懂了,确实深入浅出
kenau20102012-02-07这笔记好用!因为之前看过很多傅里叶的书,都不是很懂(本来数学基础不太好) 看这笔记的讲解,基本概念都懂了,确实深入浅出 code_robot2012-07-18这资源好!真是深入浅出呀!谢谢分享!!!!
code_robot2012-07-18这资源好!真是深入浅出呀!谢谢分享!!!!
- 粉丝: 3
- 资源: 2
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功



























