三角函数的图象与性质附答案及作业题.pdf

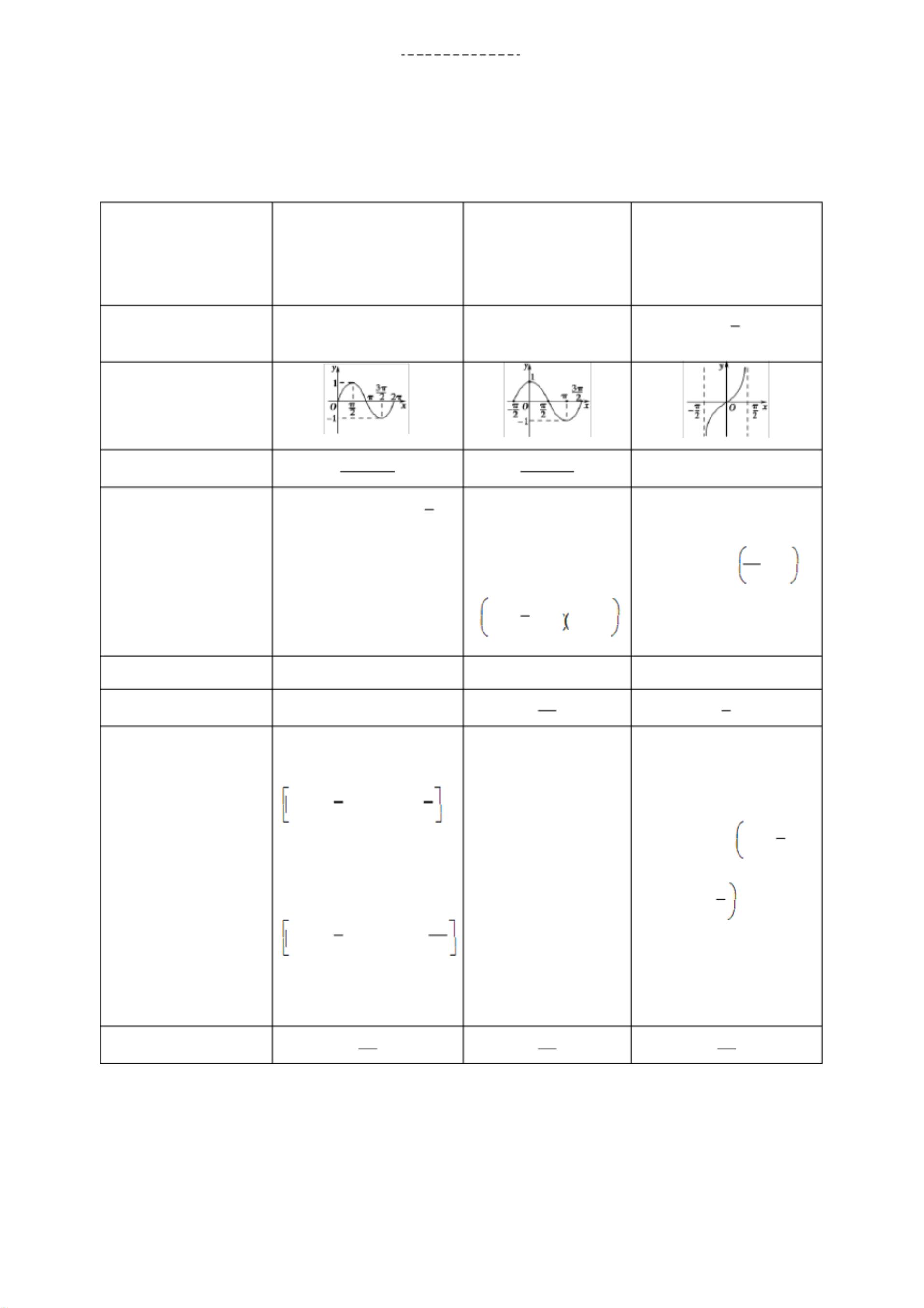
三角函数是数学中重要的基本概念，特别是在解决周期性问题、振动和波的分析等领域有着广泛的应用。本节主要探讨的是三角函数的图象与性质，包括定义域、值域、周期性、奇偶性、单调性和对称性，以及如何利用这些性质解决实际问题。 1. 定义域与值域： - 正弦函数y=sinx的定义域是全体实数R，值域是[-1, 1]。 - 余弦函数y=cosx的定义域也是R，值域同样为[-1, 1]。 - 正切函数y=tanx的定义域是{x|x≠kπ+π/2, k∈Z}，值域是整个实数R。 2. 对称性： - sinx的对称轴是x=kπ+π/2（k∈Z），对称中心是(kπ, 0)（k∈Z）。 - cosx的对称轴是x=kπ（k∈Z），对称中心是(kπ+π/2, 0)（k∈Z）。 - tanx没有对称轴，但有对称中心x=kπ/2（k∈Z）。 3. 周期性： - sinx和cosx的周期都是2π，而tanx的周期是π。 4. 单调性： - sinx的单调增区间是[2kπ-π/2, 2kπ+π/2]（k∈Z），单调减区间是[2kπ+π/2, 2kπ+3π/2]（k∈Z）。 - cosx的单调增区间是[2kπ-π, 2kπ]（k∈Z），单调减区间是[2kπ, 2kπ+π]（k∈Z）。 - tanx在整个定义域内都是单调增的。 5. 奇偶性： - sinx是奇函数，cosx是偶函数，tanx也是奇函数。 6. 求解三角函数的定义域、值域和最值： - 解三角函数的定义域通常涉及解三角不等式，可以通过画图或利用三角函数线来辅助。 - 求值域或最值时，可以将函数转化为标准形式，如Asin(ωx+φ)+k，然后利用周期性和单调性确定。 7. 三角函数的奇偶性和周期性： - 例如，y=2cos2x-π/4-1是一个最小正周期为π的偶函数。 8. 三角函数的单调性： - 求单调区间需要找出导数的正负变化，如f(x)=sin(π/2-x)在[0, π]上单调递增。 9. 对称性： - 对称轴和对称中心的确定涉及到特定的x值，例如y=cos2x+π/3的对称轴可能是x=-π/12。 10. 参数问题： - 如求解ω的值，可以根据单调区间确定，例如，如果f(x)=sinωx+π/3的单调递增区间是[kπ-5π/12, kπ+π/12](k∈Z)，那么ω=2。 通过理解和掌握以上知识，我们可以解决各种与三角函数相关的题目，包括求定义域、值域、最值，判断奇偶性和周期性，以及确定单调性和对称性等。对于更复杂的问题，可能需要结合其他数学工具，如微积分和复数理论。