Matlab辅助激光光学分析与应用（最终完整版20140512）.pdf

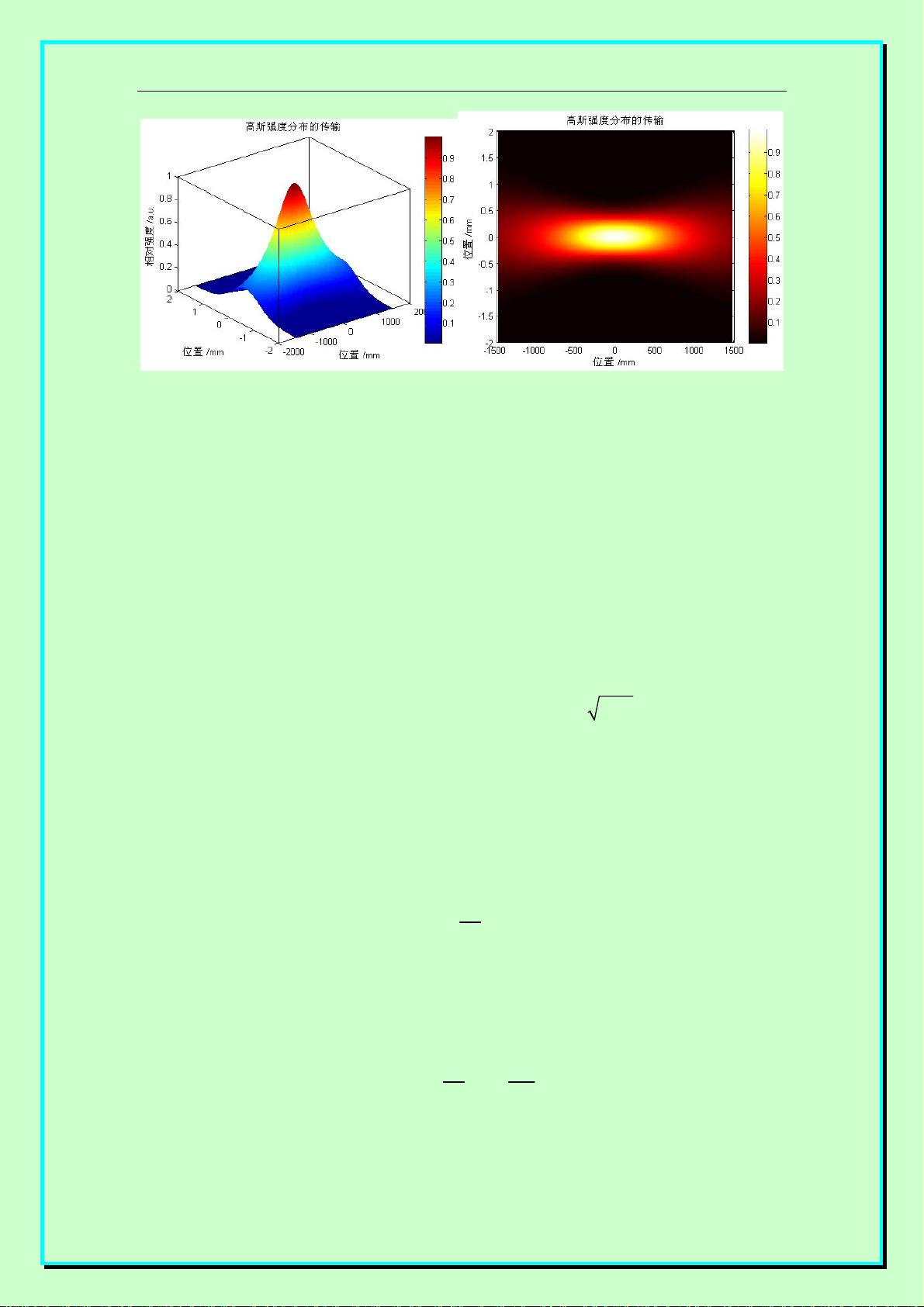
### Matlab辅助激光光学分析与应用知识点总结 #### 1.1 Maxwell方程组与电磁波理论 Maxwell方程组是电磁学领域的基石之一，它由四个方程组成，描述了电场(E)、磁场(B)与电荷(q)、电流(J)之间的关系。这四个方程分别是： 1. **高斯定律** (源自库伦定律): \(\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}\)，其中 \(\rho\) 是电荷密度，\(\varepsilon_0\) 是真空介电常数。 2. **磁性无源定律** (源自毕奥-萨瓦尔定律): \(\nabla \cdot \mathbf{B} = 0\)，说明不存在磁单极子。 3. **法拉第电磁感应定律**: \(\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}\)，描述了变化的磁场如何产生电场。 4. **安培环路定律**(含Maxwell修正项): \(\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}\)，解释了电流及变化的电场如何产生磁场。 这些方程揭示了电磁波的存在及其以光速传播的事实，从而将光学、电学与磁学统一起来。 #### 1.2 波动方程及激光传输的基本方程 基于Maxwell方程组，可以推导出波动方程。对于激光光学的应用而言，通常采用旁轴近似来简化问题。在此近似下，激光束可以视为具有高斯分布的电场复振幅： \[ E(r,z) = E_0 \exp\left[-\frac{(r^2)}{w(z)^2}\right] \exp\left[j\left(kz - \phi(z)\right)\right] \] 这里，\(E_0\) 是电场振幅，\(k\) 是波数，\(w(z)\) 和 \(\phi(z)\) 分别是与光束相关的传播参数。 - **光束半径** \(w(z)\): \[ w(z) = w_0 \sqrt{1 + \left(\frac{z}{z_R}\right)^2} \] 其中，\(w_0\) 是束腰半径，\(z_R\) 是瑞利长度。 - **相位函数** \(\phi(z)\): \[ \phi(z) = k \frac{z^2}{2z_R} - \arctan\left(\frac{z}{z_R}\right) \] 通过这些基本方程，我们可以分析激光束的传输特性，包括光束发散角等重要参数。 #### 1.3 Matlab编程实现 Matlab作为一种强大的数值计算工具，在处理激光光学问题时展现出独特的优势。例如，可以使用Matlab绘制具有高斯分布的电场强度图形。以下是一段用于绘制高斯强度分布的Matlab代码示例： ```matlab clear; clc; w0 = 0.5; r = linspace(0, 3*w0, 200); eta = linspace(0, 2*pi, 200); [rho, theta] = meshgrid(r, eta); [x, y] = pol2cart(theta, rho); Iopt = exp(-2*rho.^2/w0^2); surf(x, y, Iopt); shading interp; xlabel('位置 /mm'); ylabel('位置 /mm'); zlabel('相对强度 /a.u.'); title('高斯强度分布'); axis([-3*w0, 3*w0, -3*w0, 3*w0, 0, 1]); colorbar; colormap('hot'); box on; grid off; ``` 这段代码清晰地展示了如何利用Matlab绘制激光束的强度分布图，不仅便于理解光束的分布特征，而且有助于进一步的研究与分析。 此外，通过调整代码中的参数，还可以模拟不同条件下的激光传输情况，这对于深入研究激光光学具有重要意义。 通过Maxwell方程组及其在旁轴近似下的应用，结合Matlab的强大功能，可以有效地进行激光光学的分析与应用研究。