求解共点力平衡问题的常见方法.pdf

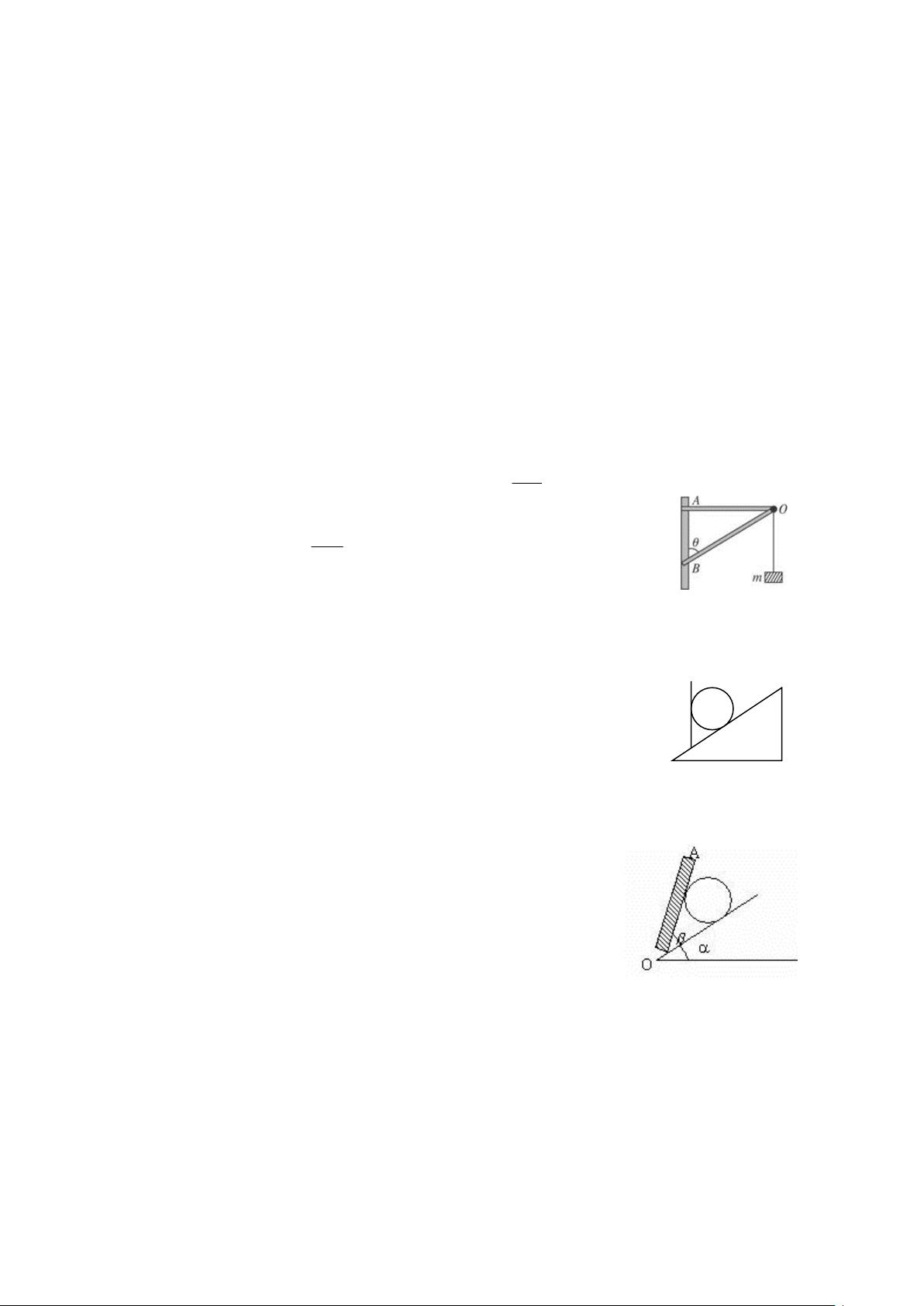
解析共点力平衡问题的常见方法 本文将介绍共点力平衡问题的常见方法，包括力的合成法、力的分解法、正交分解法、 相似三角形法、图解法、矢量三角形法、对称法、整体法与隔离法。这些方法可以帮助高一新生更好地理解和解决共点力平衡问题。 一、力的合成法 力的合成法是指物体在三个共点力的作用下处于平衡状态，则任意两个力的合力一定与第三个力大小相等，方向相反。例如，2008 年·广东卷，质量为 m 的物体悬挂在轻质支架上，斜梁 OB 与竖直方向的夹角为 θ，设水平横梁 OA 和斜梁 OB 作用于 O 点的弹力分别为 F1 和 F2。 二、力的分解法 力的分解法是在实际问题中，根据力产生的实际作用效果分解。例如，在倾角为 θ 的斜面上，放一质量为 m 的光滑小球，球被竖直的木板挡住，则球对挡板的压力和球对斜面的压力分别是多少？ 三、正交分解法 正交分解法是解多个共点力作用下物体平衡问题的方法。物体受到三个或三个以上力的作用时，常用正交分解法列平衡方程求解。例如，如图所示，重力为 500N 的人通过跨过定滑轮的轻绳牵引重 200N 的物体，当绳与水平面成60°角时，物体静止。 四、相似三角形法 相似三角形法是根据平衡条件并结合力的合成与分解的方法，把三个平衡力转化为三角形的三条边，利用力的三角形与空间的三角形的相似规律求解。例如，固定在水平面上的光滑半球半径为 R，球心 0 的正上方 C 处固定一个小定滑轮，细线一端拴一小球置于半球面上 A 点，另一端绕过定滑轮。 五、图解法 图解法是对受三力作用而平衡的物体，将力矢量图平移使三力组成一个首尾依次相接的封闭力三角形，进而处理物体平衡问题的方法。例如，如图 4 甲，细绳 AO、BO 等长且共同悬一物，A 点固定不动，在手持 B 点沿圆弧向 C 点缓慢移动过程中，绳 BO 的张力将（ ）。 六、矢量三角形法 矢量三角形法是在力的静态平衡问题中的应用。若物体受到三个力（不只三个力时可以先合成三个力）的作用而处于平衡状态，则这三个力一定能构成一个力的矢量三角形。例如，如图所示，光滑的小球静止在斜面和木版之间，已知球重为 G，斜面的倾角为 θ，求下列情况下小球对斜面和挡板的压力？ 七、对称法 对称法是研究对象所受力若具有对称性，则求解时可把较复杂的运算转化为较简单的运算，或者将复杂的图形转化为直观而简单的图形。例如，如图 10 甲所示，重为G的均匀链条挂在等高的两钩上，链条悬挂处与水平方向成角，试求链条两端的张力大小和链条最低处的张力大小。 八、整体法与隔离法 整体法与隔离法通常在分析外力对系统的作用时，用整体法；在分析系统内各物体（各部分）间相互作用时，用隔离法．例如，有一垂直支架 AOB，AO 水平放置，表面粗糙，OB 竖直向下，表面光滑，AO 上套有小环 P，OB 上套有小环 Q，两环质量均为 m，两环间由一根质量可忽略，不伸长的细绳相连，并在某一位置平衡，如图所示，现将 P 环向左移一小段距离，两环再将达到平衡，那么将移动后的平衡状态和原来的平衡状态比较，AO 杆对 P 环的支持力和细绳拉力的变化情况是（ ）。 共点力平衡问题的常见方法有力的合成法、力的分解法、正交分解法、相似三角形法、图解法、矢量三角形法、对称法、整体法与隔离法等。这些方法可以帮助高一新生更好地理解和解决共点力平衡问题。