数据结构课程设计-计算器.doc

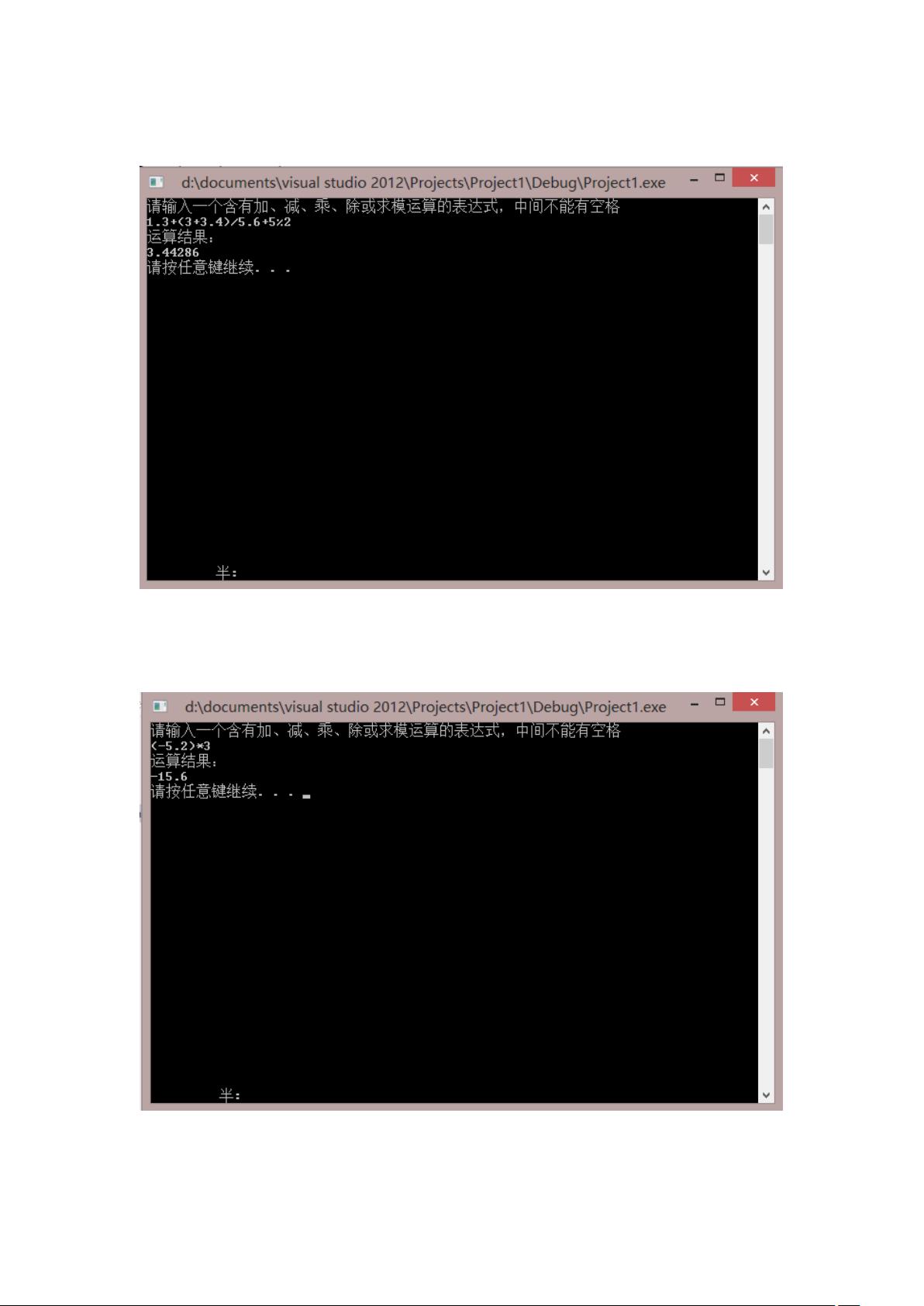
数据结构课程设计报告 实验一：计算器 设计要求 1、问题描述：设计一个计算器，可以实现计算器的简单运算，输出并检验结果的 正确性，以及检验运算表达式的正确性。 2、输入：不含变量的数学表达式的中缀形式，可以接受的操作符包括+、- 、*、/、%、(、)。 具体事例如下： 输出：如果表达式正确，则输出表达式的正确结果；如果表达式非法，则输出错误信息 。 具体事例如下： 知识点：堆栈、队列 实际输入输出情况： 正确的表达式 对负数的处理 表达式括号不匹配 表达式出现非法字符 表达式中操作符位置错误 求余操作符左右出现非整数 其他输入错误 数据结构与算法描述 解决问题的整体思路： 将用户输入的中缀表达式转换成后缀表达式，再利用转换后的后缀表达式进行计 算得出结果。 解决本问题所需要的数据结构与算法： 用到的数据结构是堆栈。主要算法描述如下： A．将中缀表达式转换为后缀表达式： 1. 将中缀表达式从头逐个字符扫描，在此过程中，遇到的字符有以下几种情况： 1）数字 2）小数点 3）合法操作符+ - * / % 4）左括号 5）右括号 6）非法字符 2. 首先为操作符初始化一个map<std::st 数据结构课程设计的目标是设计一个计算器程序，该程序能够接收不含变量的中缀数学表达式，支持基础算术运算，并能正确处理各种错误情况。在这个项目中，主要涉及的两个核心知识点是堆栈和队列。 堆栈是解决这个问题的关键数据结构。在计算中缀表达式时，首先需要将中缀表达式转换为后缀表达式，也就是所谓的逆波兰表示法。堆栈在这里用于存储运算符。在处理中缀表达式的过程中，遇到数字和小数点直接添加到结果中，遇到操作符时则根据优先级规则决定是否将其压入堆栈。具体来说，当遇到一个新操作符时，如果堆栈顶的操作符优先级低于新操作符，那么就将堆栈顶的操作符弹出并添加到结果中，直到遇到一个优先级更低的操作符或左括号为止。遇到左括号时，直接压入堆栈；遇到右括号时，将从栈顶开始弹出所有非左括号的元素，直到遇到一个左括号。这个过程可以确保正确处理嵌套的括号。 在处理过程中，还需要检查输入的合法性，如检查括号是否匹配、操作符的位置是否正确、是否有连续的操作符、运算符两侧是否有数字等。例如，如果遇到连续的操作符，这意味着输入错误，程序应给出相应的错误提示。同样，如果运算符的右侧缺少运算数，或者以运算符开头，也需要返回错误信息。对于负数的处理，如果用户尝试在运算符前加减号，可以先在结果中添加一个0，以确保负号被正确处理。 算法的主要步骤如下： 1. 初始化一个堆栈`sym`用于存放操作符，并创建一个优先级映射`priority`，存储每个操作符的优先级。 2. 从输入的中缀表达式开始遍历，根据字符类型执行相应操作： - 数字和小数点直接添加到结果`to`中。 - 当遇到操作符时，检查其前后是否符合语法规则，然后根据优先级决定是否压栈或弹栈。 - 遇到左括号`(`时，直接压栈；遇到右括号`)`时，弹栈并检查括号匹配。 - 如果遇到非法字符，输出错误信息并停止处理。 3. 遍历结束后，将堆栈中剩余的操作符全部弹出并添加到结果中，因为它们都是左括号或者优先级更高的操作符。 完成上述步骤后，得到的后缀表达式可以通过简单的遍历计算得出最终结果，因为后缀表达式中，运算符的执行顺序已经明确，只需要依次计算即可。 这个设计不仅可以帮助学生理解数据结构中的堆栈应用，还能让他们掌握中缀到后缀表达式的转换，以及如何处理和识别错误的数学表达式。通过这个课程设计，学生可以提升编程技能，特别是处理复杂逻辑和错误检查的能力。