数据结构 1.试写一算法,实现单链表的就地逆置(要求在原链表上进行)。 void converse(NODEPTR L) { NODEPTR p,q; P=L ->next; q=p ->next; L ->next=NULL; while(p) /*对于当前结点p,用头插法将结点p插入到头结点之后*/ { p ->next=L ->next; L ->next= p; p=q; q=q ->next; } } 2.以数据集{4,5,6,7,10,12,18}为结点权值,画出构造的哈弗曼树,计算其带权路径长 度。 其带权路径长度为 62 3.假设一棵二叉树如下图所示,求: 1. 该二叉树的深度; 2. 该二叉树的先序序列 3. 该二叉树的中序序列; 4. 该二叉树的后续序列。 1. 二叉树的深度:h=6。 2. 二叉树的先序序列:EBADCFHGIKJ 3. 二叉树的中序序列:ABCDEFGHIJK 4. 二叉树的后序序列:ACDBGJKIHFE 4.已知图7.1所示的有向图,请给出该图的 每个顶点的入/出度; 邻接矩阵; 邻接表; 逆邻接表; 图7.1 (1) 顶点 "A "B "C
数据结构是计算机科学中的核心概念,它涉及到如何有效地组织和管理数据,以便高效地执行各种操作。本文件中提到了几种关键的数据结构及其操作。
我们讨论的是单链表的就地逆置。单链表是一种线性数据结构,其中每个节点包含数据和指向下一个节点的指针。在给定的算法`converse(NODEPTR L)`中,通过头插法实现了链表的逆置。头插法是将新节点插入到链表头部的方法。算法的步骤如下:
1. 设置两个指针`p`和`q`,分别指向第二个节点和第三个节点。
2. 将头节点的`next`指针设为`NULL`,准备接收新的链表头部。
3. 使用循环遍历链表,每次循环将`p`指向的节点插入到头节点之后,然后移动`p`和`q`指向下一个节点。
4. 循环结束后,原链表已经被逆置。
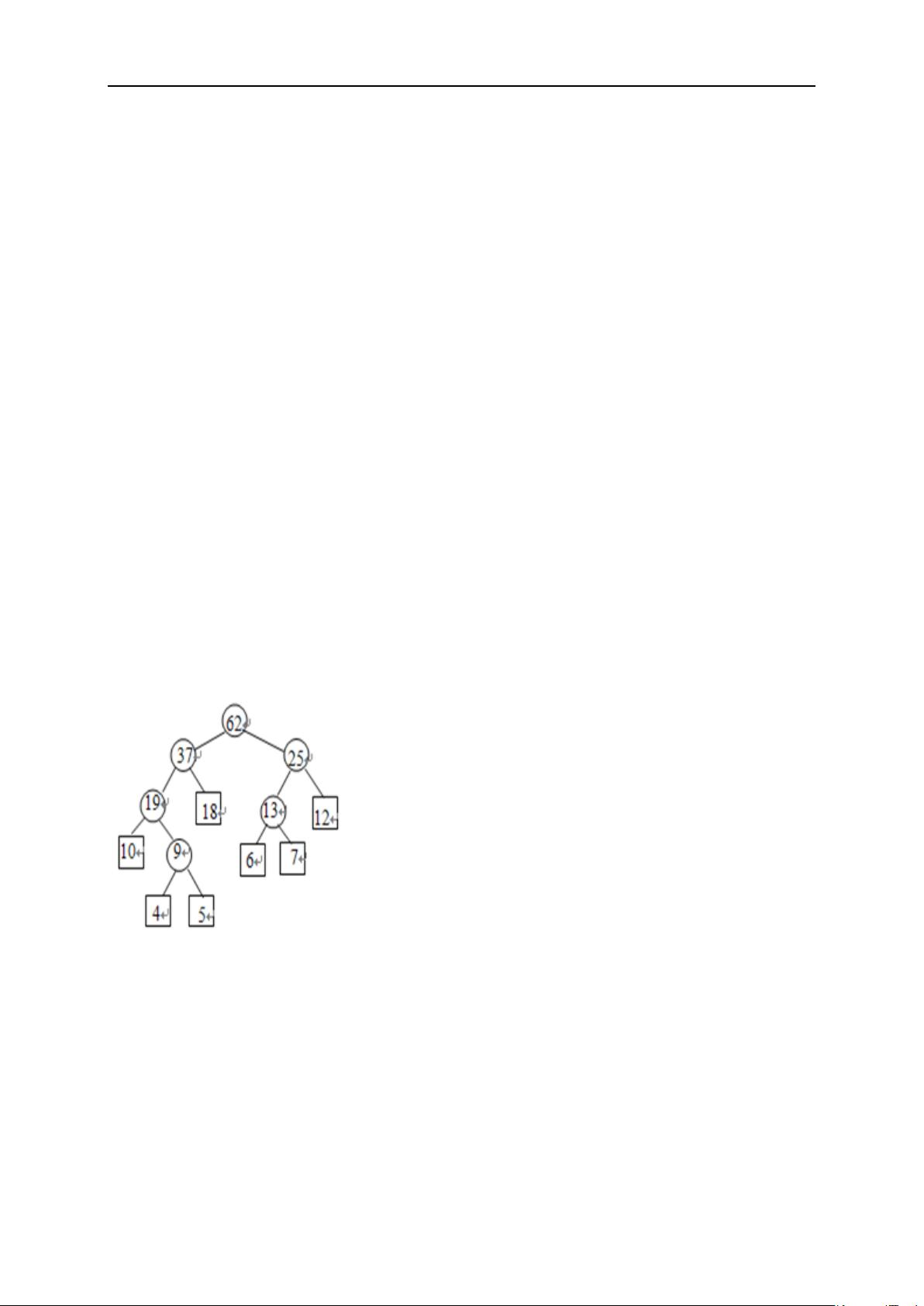
接下来,涉及到了哈弗曼树的构建。哈弗曼树是一种特殊的二叉树,用于实现最优的前缀编码,常用于数据压缩。给定权重集合{4,5,6,7,10,12,18},我们需要构建相应的哈弗曼树,并计算其带权路径长度。哈弗曼树的构建原则是每次都合并权重最小的两个节点,直到所有节点都合并成一个根节点。带权路径长度是所有叶子节点的权重与其到根节点的路径长度乘积之和,已知为62。
第三部分,我们考虑了一棵特定的二叉树。二叉树的深度是树中最长路径上的节点数,这里是6。先序遍历(根-左-右)的顺序是EBADCFHGIKJ,中序遍历(左-根-右)的顺序是ABCDEFGHIJK,后序遍历(左-右-根)的顺序是ACDBGJKIHFE。
第四部分,讨论了有向图的相关信息。图的顶点入度和出度表示指向该顶点的边的数量和从该顶点出发的边的数量。图7.1中,顶点A的入度是1,出度是2,以此类推。邻接矩阵是表示图中节点间连接的二维数组,邻接表则以列表形式存储每个节点的邻接节点。逆邻接表是邻接表的反向版本,存储每个节点的出边指向的节点。
此外,还提到了对图7.2的深度优先搜索(DFS)和广度优先搜索(BFS)遍历,DFS从顶点1开始得到的遍历序列是1→2→4→8→5→3→6→7,而BFS的遍历序列是1→2→3→4→5→6→7→8。
提到了几种排序算法的实例。起泡排序、直接插入排序、希尔排序、树形选择排序、堆排序和归并排序是常见的排序算法。每种排序算法的示例展示了每趟排序后关键字的状态,例如起泡排序的每趟交换使得较大元素逐渐“浮”到序列末尾。
这些知识点涵盖了数据结构的基本操作,包括链表操作、树的遍历、图的表示以及排序算法的实践应用,这些都是计算机科学基础课程的重要内容。