有限元 matlab 习题4.15.pdf

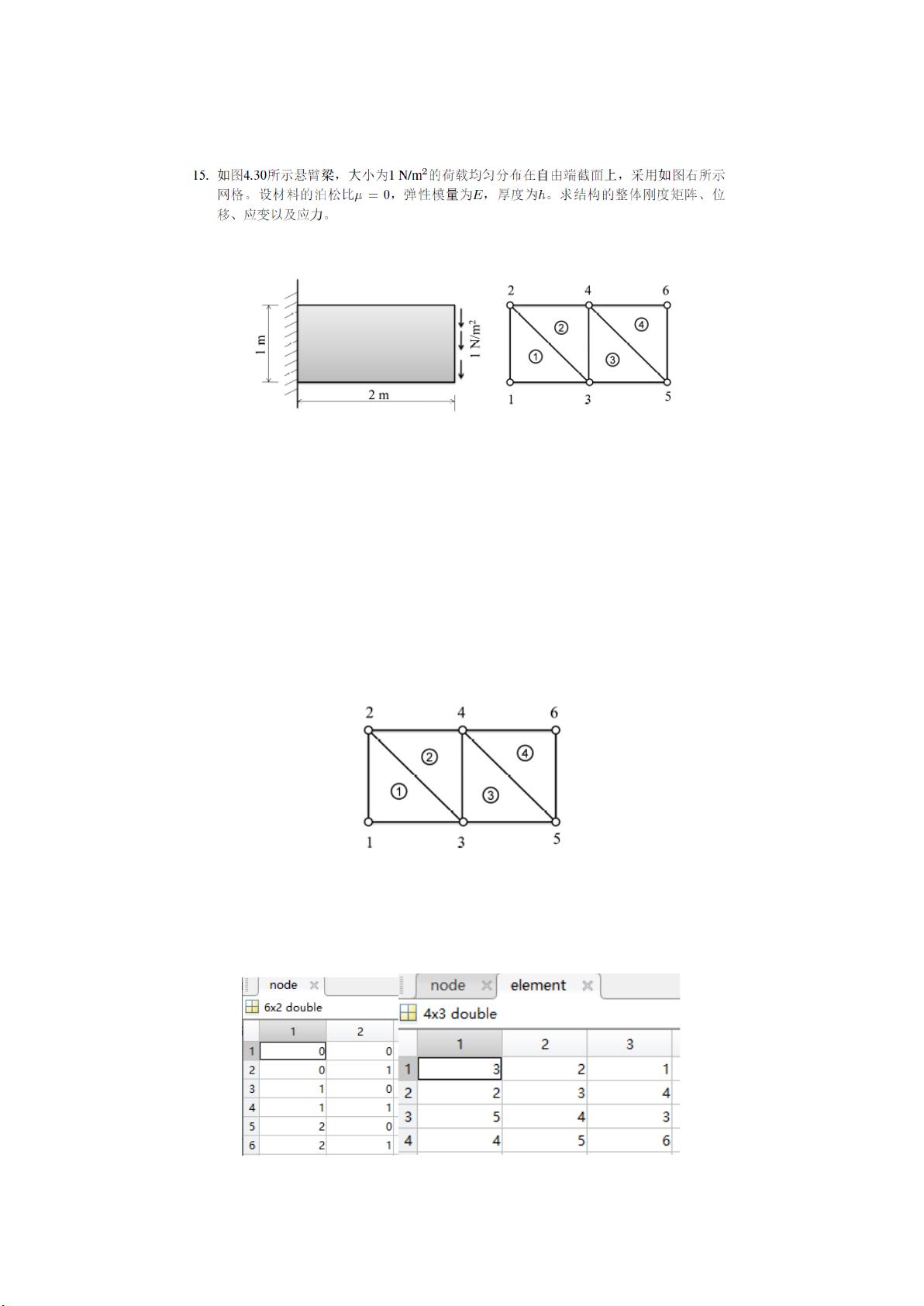
【有限元方法与MATLAB应用】\n\n本题是一道关于有限元法的应用题，主要涉及MATLAB编程，用于解决一维悬臂梁的结构分析问题。悬臂梁受到大小为1N/m²的均布荷载作用，荷载位于梁的自由端。采用特定的网格划分对梁进行离散化，然后通过单元分析、单元组装和边界条件的引入，求解结构的整体刚度矩阵，计算位移、应变和应力，并绘制变形图。\n\n1. **网格划分**\n题目中提到的网格划分是有限元方法的第一步，用于将连续的结构域分解为多个互不重叠的子区域，即单元。在这个例子中，悬臂梁被划分为多个三角形单元。在MATLAB中，结点编号和单元连接关系可以通过`node`和`element`数组来表示。例如，`node`数组包含了所有结点的坐标，`element`数组则定义了每个单元的结点连接关系。\n\n2. **单元分析**\n单元分析涉及计算每个单元的刚度矩阵。对于题目中的二维三角形单元，当泊松比μ=0时，所有单元的刚度矩阵可以通过旋转已知单元的刚度矩阵180度得到。刚度矩阵`Ke`由弹性模量`E`、几何参数`h`和形状函数计算得出。在MATLAB中，`Element_stiff_tri2D`函数用于计算单元刚度矩阵，输入参数包括弹性矩阵`D`（在形心处）、结点坐标`coords`、单元厚度`h`。\n\n3. **单元组装**\n单元组装是将所有单元的刚度矩阵组合成整体刚度矩阵`Kglobal`的过程。这个过程遵循“对号入座”的原则，即将每个单元的刚度矩阵按结点编号在整体刚度矩阵中正确放置。MATLAB中的`Plain_stiff`函数实现了这一过程，同时也处理了体积力引起的单元节点力向量`Fe`，并将边界位移条件引入到系统中。\n\n4. **边界条件与求解**\n由于悬臂梁的自由端受到荷载，因此需要对边界条件进行处理。通常情况下，这涉及到对某些结点的位移进行固定或设置为已知值。在MATLAB中，这通常通过修改整体刚度矩阵和载荷向量来实现。求解系统方程后，可以得到所有结点的位移。\n\n5. **计算应变和应力**\n一旦得到位移，可以利用单元刚度矩阵和结点位移来计算单元内的应变和应力。应变通常是位移的线性导数，而应力则是应变与材料属性的函数。在MATLAB中，这可以通过进一步的计算或自定义函数完成。\n\n6. **绘制变形图**\n最后一步是绘制结构的变形图，以直观地展示结构在荷载下的响应。这通常通过将位移数据转换为几何坐标变化，然后用MATLAB的绘图功能来实现。\n\n该题目的解决涉及了有限元分析的基本流程，包括几何建模、网格划分、单元分析、单元组装、边界条件处理、求解线性系统以及后处理。在MATLAB中，这些问题可以通过编写程序脚本来实现，从而实现自动化分析。