没有合适的资源?快使用搜索试试~ 我知道了~
深度生成模型可以分为有监督与无监督,主要还是在于无监督地应用,用于在没有目标类标签信息的情况下捕捉观测到或可见数据的高阶相关性,可以通过从网络中采样来生成有效样本,譬如受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)、深度信念网络(Deep Belief Network, DBN)、深度玻尔兹曼机(Deep Boltzmann Machine, DBM)和广义除噪自编码器(Generalized Denoising Autoencoders)。
资源推荐
资源详情
资源评论

第 13 章 深度生成模型
我不能创造的东西,我就不了解。
— 理查德·菲利普·费曼
概率生成模型,简称生成模型(Generative Model),是概率统计和机器学
习中的一类重要模型,指一系列用于随机生成可观测数据的模型。假设在一个
连续的或离散的高维空间 X 中,存在一个随机向量 X 服从一个未知的数据分布
p
r
(x), x ∈ X。生成模型是根据一些可观测的样本 x
(1)
, x
(2)
, ··· , x
(N)
来学习一
个参数化的模型 p
θ
(x) 来近似未知分布 p
r
(x),并可以用这个模型来生成一些样
本,使得“生成”的样本和“真实”的样本尽可能地相似。
生成模型的应用十分广泛,可以用来不同的数据进行建模,比如图像、文
本、声音等。比如图像生成,我们将图像表示为一个随机向量 X,其中每一维
都表示一个像素值。假设自然场景的图像都服从一个未知的分布p
r
(x),希望通
过一些观测样本来估计其分布。高维随机向量一般比较难以直接建模,需要通
过一些条件独立性来简化模型。但是,自然图像中不同像素之间的存在复杂的
依赖关系(比如相邻像素的颜色一般是相似的),很难用一个明确的图模型来描
述其依赖关系,因此直接建模 p
r
(x) 比较困难。
深度生成模型就是利用深层神经网络可以近似任意函数的能力来建模一个
复杂的分布 p
r
(x)。假设一个随机向量 Z 服从一个简单的分布 p(z), z ∈ Z(比
如标准正态分布),我们使用一个深层神经网络 g : Z → X,并使得 g(z) 服从
p
r
(x)。
本章介绍两种深度生成模型:变分自动编码器 [Kingma and Welling, 2013,
Rezende et al., 2014] 和对抗生成式网络 [Goodfellow et al., 2014]。
13.1 概率生成模型
生成模型一般具有两个基本功能:密度估计和生成样本。
312 2019 年 4 月 6 日 第 13 章 深度生成模型
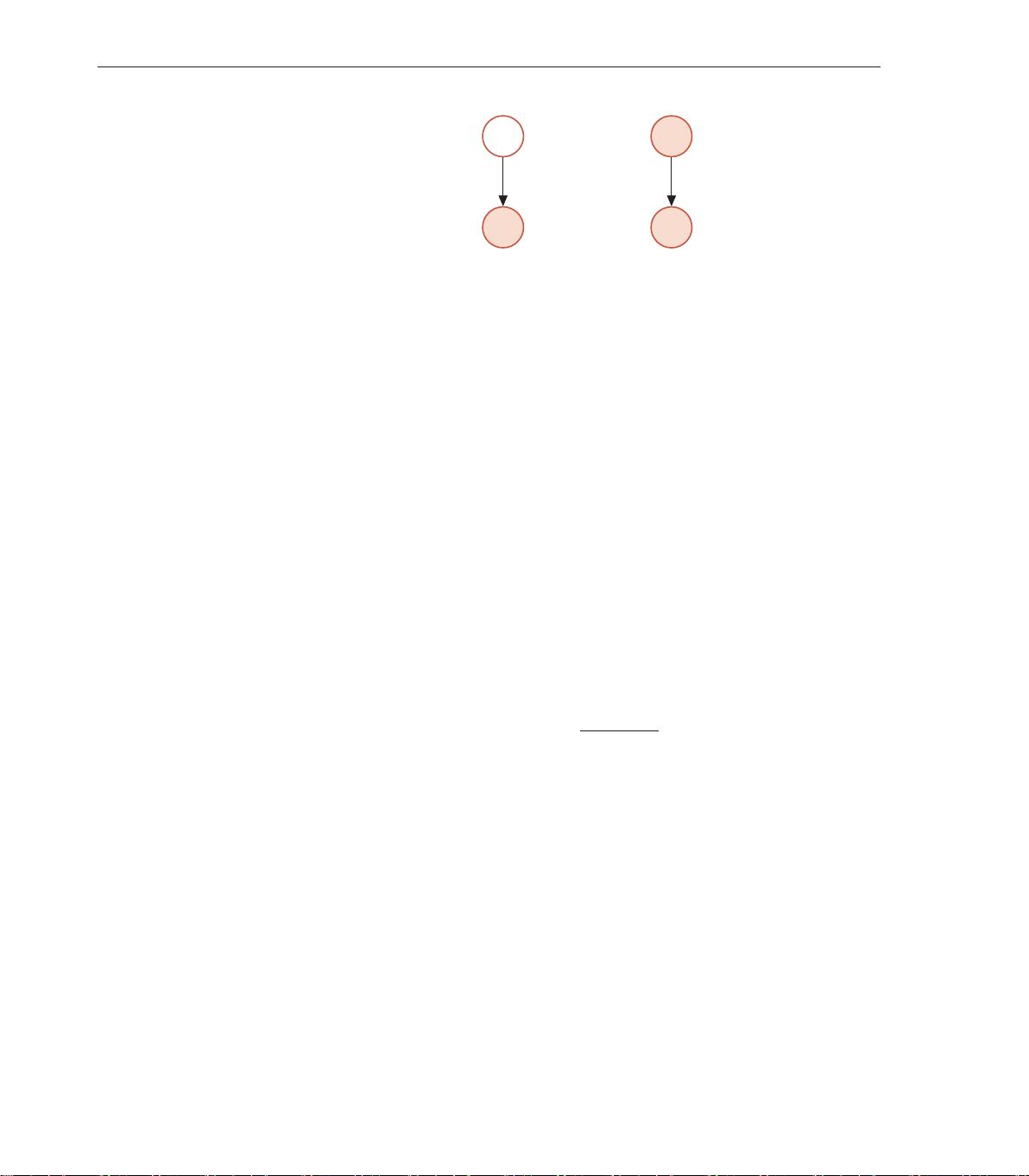
z
x
(a) 带隐变量的生成模型
y
x
(b) 带类别的生成模型
图 13.1 生成模型
13.1.1 密度估计
给定一组数据 D = {x
(i)
}, 1 ≤ i ≤ N,假设它们都是从独立地从相同的概
率密度函数为 p
r
(x) 的未知分布中产生的。密度估计(Density Estimation)是
根据数据集 D来估计其概率密度函数 p
θ
(x)。
在机器学习中,密度估计是一种非常典型的无监督学习问题。如果要建模
密度估计参见第9.2节。
的分布包含隐变量(如图13.1a),比如高斯混合模型,就需要利用 EM 算法来进
行密度估计。
EM 算法参见第11.4.2.1节。
13.1.1.1 应用于监督学习
生成模型也可以应用于监督学习。监督学习的目标是建模输出标签的条件
概率密度函数 p(y|x )。根据贝叶斯公式,
p(y|x) =
p(x, y)
y
p(x, y)
. (13.1)
我们可以将监督学习问题转换为联合概率密度函数 p(x, y) 的密度估计问题。
图13.1a给出了生成模型用于监督学习的图模型表示。在监督学习中,比较
典型的生成模型有朴素贝叶斯分类器、隐马尔可夫模型
判别模型 和生成模型相对应的另一类监督学习模型是判别模型(Discriminative
Model)。判别式模型直接建模条件概率密度函数 p(y|x),并不建模其联合概率
密度函数 p(x, y)。常见的判别模型有 logistic 回归、支持向量机、神经网络等。
由生成模型可以得到判别模型,但由判别模型得不到生成模型。
13.1.2 生成样本
生成样本就是给定一个概率密度函数为 p
θ
(x) 的分布,生成一些服从这个
分布的样本,也称为采样。我们在第11.3节中介绍了一些常用的采样方法。
采样方法参见第11.3节。
邱锡鹏:《神经网络与深度学习》 https://nndl.github.io/

13.2 变分自编码器 2019 年 4 月 6 日 313
z
ϕ
θ
x
N
图 13.2 变分自编码器。实线表示生成模型,虚线表示变分近似。
对于图13.1a中的图模型,在得到 p(z, θ) 和 p(x|z, θ) 之后,我们就可以生成
数据 x,具体过程可以分为两步进行:
1. 根据隐变量的先验分布 p(z, θ) 进行采样,得到样本 z;
2. 根据条件分布 p(x|z, θ) 进行采样,得到 x。
因此在生成模型中,重点是估计条件分布 p(x|z, θ)。
13.2 变分自编码器
13.2.1 含隐变量的生成模型
假设一个生成模型(如图13.2所示)中包含隐变量,即有部分变量是不可观
测的,其中观测变量 X 是一个高维空间 X 中的随机向量,隐变量 Z 是一个相对
低维的空间 Z 中的随机向量。这个生成模型的联合概率密度函数可以分解为
本章中,我们假设 X 和 Z 都
是连续随机向量。
p(x, z|θ) = p(x|z, θ)p(z|θ), (13.2)
其中 p(z|θ) 为隐变量 z 先验分布的概率密度函数,p(x|z, θ) 为已知 z 时观测变量
x 的条件概率密度函数,θ 表示两个密度函数的参数。一般情况下,我们可以假
设 p(z|θ) 和 p(x|z, θ) 为某种参数化的分布族,比如正态分布。这些分布的形式
已知,只是参数 θ 未知,可以通过最大化似然来进行估计。
给定一个样本 x,其对数边际似然 log p(x|θ) 可以分解为
log p(x|θ) = ELBO(q, x|θ, ϕ) + D
KL
(q(z|ϕ)∥p(z|x, θ)), (13.3)
其中 q(z|ϕ) 是额外引入的变分密度函数,其参数为 ϕ,ELBO(q, x|θ, ϕ) 为证据
参见公式 (11.96)。
邱锡鹏:《神经网络与深度学习》 https://nndl.github.io/

314 2019 年 4 月 6 日 第 13 章 深度生成模型
下界,
ELBO(q, x|θ, ϕ) = E
z∼q( z|ϕ)
log
p(x, z|θ)
q(z|ϕ)
. (13.4)
最大化对数边际似然 log p(x|θ) 可以用 EM 算法来求解,具体可以分为两步:
EM 算法
参见第11.4.2.1节。
• E-step: 寻找一个密度函数q(z|ϕ)使其等于或接近于后验密度函数p(z|x, θ);
• M-step: 保持 q(z|ϕ) 固定,寻找 θ 来最大化 ELBO(q, x|θ, ϕ)。
这样个步骤不断重复,直到收敛。
在 EM 算法的每次迭代中,理论上最优的 q(z|ϕ) 为隐变量的后验概率密度
函数 p(z|x, θ),
p(z|x, θ) =
p(x|z, θ)p(z|θ)
z
p(x|z, θ)p(z|θ)dz
. (13.5)
后验密度函数 p(z|x, θ) 的计算是一个统计推断问题,涉及到积分计算。当隐变
量 z 是有限的一维离散变量,则计算起来比较容易。在一般情况下,这个后验概
率密度函数是很难计算的。此外,概率密度函数 p(x|z, θ) 一般也比较复杂,很
难直接用已知的分布族函数进行建模。
变分自编码器(Variational Autoencoder,VAE)是一种深度生成模型,其
思想是利用神经网络来分别建模两个复杂的条件概率密度函数。
1. 用神经网络来产生变分分布 q(z|ϕ),称为推断网络。理论上 q(z|ϕ) 可以不
依赖 x。但由于 q(z|ϕ) 的目标是近似后验分布 p(z|x, θ),其和 x 相关,因
此变分密度函数一般写为 q(z|x, ϕ)。推断网络的输入为 x,输出为变分分
布 q(z|x , ϕ)。
2. 用神经网络来产生概率分布 p(x|z, θ),称为生成网络。生成网络的输入为
z,输出为概率分布 p(x|z, θ)。
将推断网络和生成网络合并就得到了变分自编码器的整个网络结构,如
图13.3所示,其中实线表示网络计算操作,虚线表示采样操作。
邱锡鹏:《神经网络与深度学习》 https://nndl.github.io/
剩余22页未读,继续阅读
资源评论

白杨树~
- 粉丝: 52
- 资源: 21
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- Alook浏览器安卓版(8倍速手机浏览器)v9.5.0.mp4
- Avast清理 Avast Cleanup v24.22.0高级版.mp4
- Apt Full(AI生产力工具v2.7.1.0绿色无需联网.mp4
- 01-03-若依表结构.xmind
- AZ屏幕录制工具Screen Recorder v6.3.6高级版.mp4
- 【本体】Internet Download Manager v6.42.26.zip
- Bing Wallpaper微软壁纸v2.0.1.4 中文多语版.mp4
- bsod蓝屏伪装者v1.0单文件版.mp4
- B站0粉代码强开自动回复-附源代码.mp4
- Canvas制作的粒子十秒倒计时HTML源码.mp4
- B站视频下载器 v2024.12.11小工具软件.mp4
- Complete Internet Repair 网络修复工具v11.1.3.mp4
- Converter视频音频转换器v2.2.5.2解锁VIP版.mp4
- CPU-Z处理器相关系统信息识别v2.13.0单文件.mp4
- pdf-reader.zip
- DNS快捷工具箱轻量高性能DNS服务器工具.mp4
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功