语音滤波设计示例1.pdf

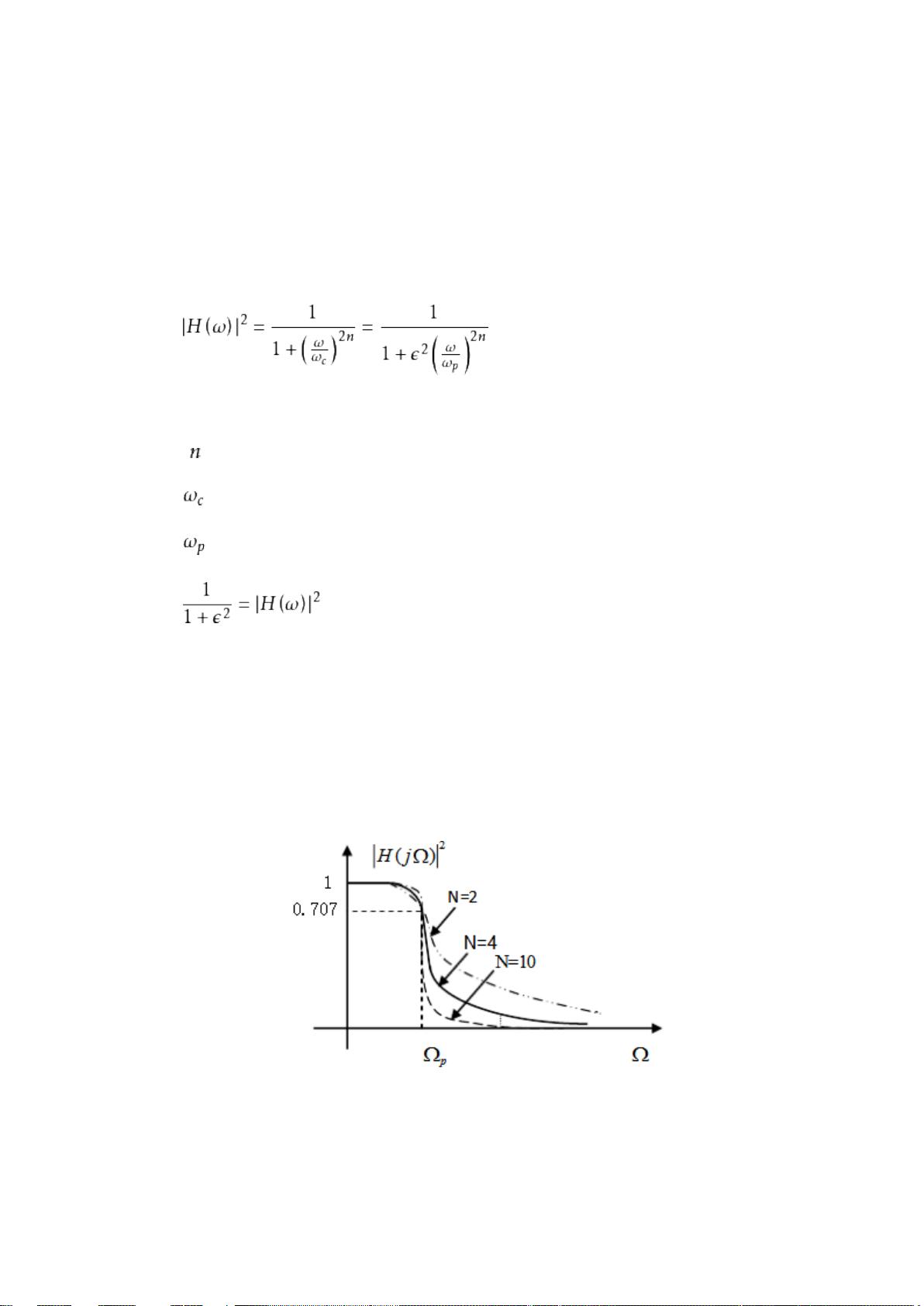
### 语音滤波设计示例知识点详解 #### 实验背景及目标 本次实验旨在通过MATLAB编程实现语音信号处理中的低通滤波器设计。实验的主要目的是去除语音信号中的高频噪声，以提升语音质量。 #### 实验工具 - **MATLAB R2016b**: MATLAB 是一种高级编程语言，特别适用于数学计算、算法开发和数据分析等领域。本实验使用的是MATLAB R2016b版本。 #### 实验原理 **数字滤波器分类** - **经典滤波器**: 其特点是将信号中有用的频率成分与需要滤除的频率成分分开处理。适用于两者频谱不重叠的情况。 - **现代滤波器**: 当信号与干扰频谱重叠时使用，如维纳滤波器、卡尔曼滤波器、自适应滤波器等。这些滤波器根据信号的统计特性进行滤波。 **滤波器类型** - **巴特沃斯低通滤波器**: 特点是在通频带内频率响应曲线尽可能平坦，在阻频带则逐渐下降至零。其振幅平方与频率的关系可通过公式表示。 - **切比雪夫低通滤波器**: 这种滤波器过渡带衰减较快，但在通频带内可能存在幅度波动。根据波动位置不同分为I型和II型。 - **I型切比雪夫滤波器**: 在通频带上存在等波纹波动。 - **II型切比雪夫滤波器**: 在阻频带上存在等波纹波动，通频带内无幅度波动。 - **窗函数法**: 用于设计FIR滤波器的方法之一，通过与窗函数相乘来实现对信号的截断。 - **汉宁窗**: 可以消除高频干扰和漏能，适用于非周期性信号。 - **凯塞窗**: 参数可调的窗函数，可以通过调整β值在主瓣宽度和旁瓣衰减之间做出平衡。 #### 实验步骤与成果展示 **实验过程** 1. **原始信号**: 首先获取待处理的语音信号。 2. **混入高斯加性白噪声**: 将噪声添加到原始语音信号中，模拟实际环境下的噪声污染情况。 3. **滤波处理**: - **巴特沃斯低通滤波器**: 使用巴特沃斯低通滤波器去除高频噪声。 - **切比雪夫低通滤波器**: 分别采用I型和II型切比雪夫滤波器进行滤波。 - **窗函数法**: - **汉宁窗**: 应用汉宁窗技术进一步改善滤波效果。 - **凯塞窗**: 调整凯塞窗的参数β以优化滤波性能。 **成果展示** - **原始信号与处理后信号对比**: - 原始信号: 显示原始语音信号波形。 - 处理后信号: 展示使用各种滤波器处理后的信号波形，并进行比较。 - **滤波器性能评估**: - 振幅响应: 绘制各种滤波器的振幅响应图，观察通带和阻带的特性。 - 相位响应: 分析滤波器的相位响应，确保信号不失真。 - 时域响应: 比较滤波前后的时域信号，直观感受滤波效果。 通过以上实验步骤和成果展示，不仅能够深入了解不同类型的滤波器及其工作原理，还能掌握MATLAB在信号处理领域的应用技巧。这对于提高语音信号的质量、改善通信系统的性能等方面具有重要意义。