五大常用算法:回溯算法,算法数据结构
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
回溯算法是一种重要的搜索策略,尤其在解决组合优化问题中广泛应用。它通过尝试所有可能的解决方案路径,并在遇到无效或不满足条件的情况时回溯,以寻找其他可能的解。回溯法通常与数据结构结合使用,如数组、栈、队列等,以有效地存储和操作中间状态。 在八皇后问题中,回溯算法的应用非常直观。问题要求在8x8的棋盘上放置8个皇后,使得任意两个皇后都不能在同一行、同一列或同一对角线上。回溯法通过逐行放置皇后并检查冲突来解决这个问题。当在某一行无法找到合适的皇后位置时,算法会回溯到上一行,尝试改变上一个皇后的位置以寻找新的解决方案。八皇后问题的代码展示了这一过程,其中`queen`函数递归地尝试放置皇后,`isOk`函数检查当前位置是否安全,而`total`变量记录有效的解决方案数量。 另一个回溯法的经典例子是0-1背包问题。给定一组物品,每件物品有重量`Wi`和价值`Pi`,以及一个有限的背包容量`c`,目标是选择物品以最大化背包中的总价值,但物品不可分割。解决0-1背包问题的关键在于定义解空间(所有可能的物品选择组合)和设计回溯策略来遍历这个空间。算法通常从第一件物品开始,决定取或不取,然后递归地处理下一个物品。如果当前选择导致背包容量超出限制或无法进一步增加总价值,就会回溯并尝试不同的选择。 在实际应用中,回溯算法通常与其他数据结构和算法技术结合使用,例如剪枝(pruning)来减少无效搜索,动态规划(dynamic programming)来避免重复计算,以及贪心策略(greedy strategy)来简化问题。这些方法可以提高回溯算法的效率,使其在处理复杂问题时更加实用。 总结来说,回溯算法是一种解决问题的有效工具,特别是在面临多种可能的决策路径且需要在路径无效时能回退到先前状态的问题上。通过与数据结构的巧妙结合,它可以解决许多实际问题,如八皇后问题和0-1背包问题。在编程竞赛和实际工程中,掌握回溯算法及其变体是提升问题解决能力的关键。
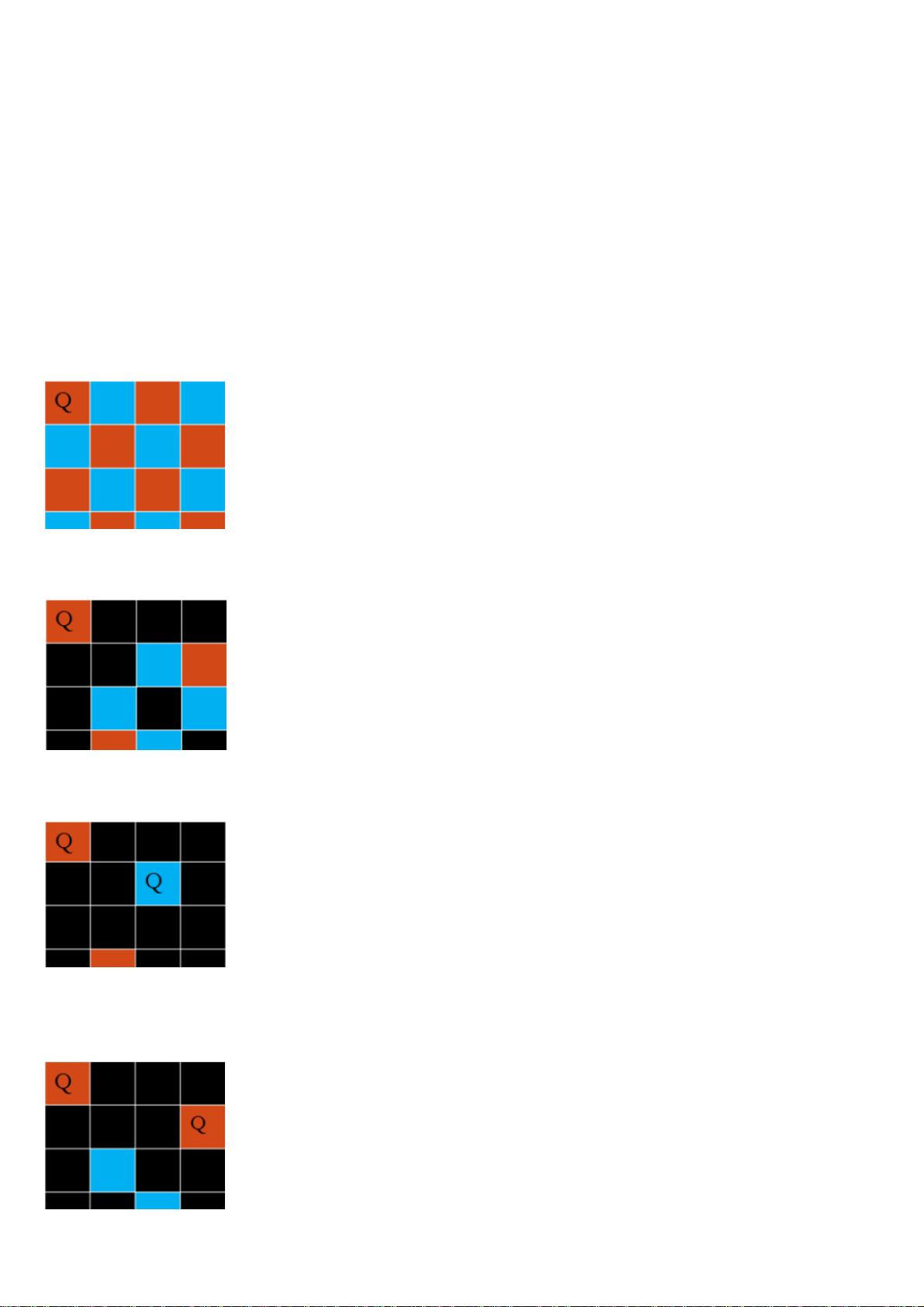

剩余7页未读,继续阅读

- 粉丝: 31
- 资源: 1万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功