没有合适的资源?快使用搜索试试~ 我知道了~
计算理论导引第二版 作者: Michael Sipser 课后答案
资源推荐
资源详情
资源评论

计算理论习题解答
练习
1.1 图给出两台 DFA M
1
和 M
2
的状态图. 回答下述有关问题.
a. M
1
的起始状态是 q
1
b. M
1
的接受状态集是{q
2
}
c. M
2
的起始状态是 q
1
d. M
2
的接受状态集是{q
1
,q
4
}
e. 对输入 aabb,M
1
经过的状态序列是 q
1
,q
2
,q
3
,q
1
,q
1
f. M
1
接受字符串 aabb 吗?否
g. M
2
接受字符串 ε 吗?是
1.2 给出练习 2.1 中画出的机器 M
1
和 M
2
的形式描述.
M
1
=(Q
1
,Σ,δ
1
,q
1
,F
1
) 其中
1)Q
1
={q
1
,q
2
,q
3
,};
2)Σ={a,b};
3)δ
1
为:
a b
q
1
q
2
q
3
q
2
q
1
q
3
q
3
q
2
q
1
4)q
1
是起始状态
5)F
1
={q
2
}
M
2
=(Q
2
,Σ,δ
2
,q
2
,F
2
) 其中
1)Q
2
={q
1
,q
2
,q
3
,q
4
};
2)Σ={a,b};
3)δ
2
为:
a b
q
1
q
2
q
3
q
4
q
1
q
2
q
3
q
4
q
2
q
1
q
3
q
4
3)q
2
是起始状态
4)F
2
={q
1
,q
4
}
1.3 DFA M 的形式描述为 ( {q
1
,q
2
,q
3
,q
4
,q
5
},{u,d},δ,q
3
,{q
3
}),其中 δ 在表 2-3 中给出。试画出此机
器的状态图。
- 1 -
q
1
q
5
q
4
q
2
q
3
u
d
u u u u
d
dd
d
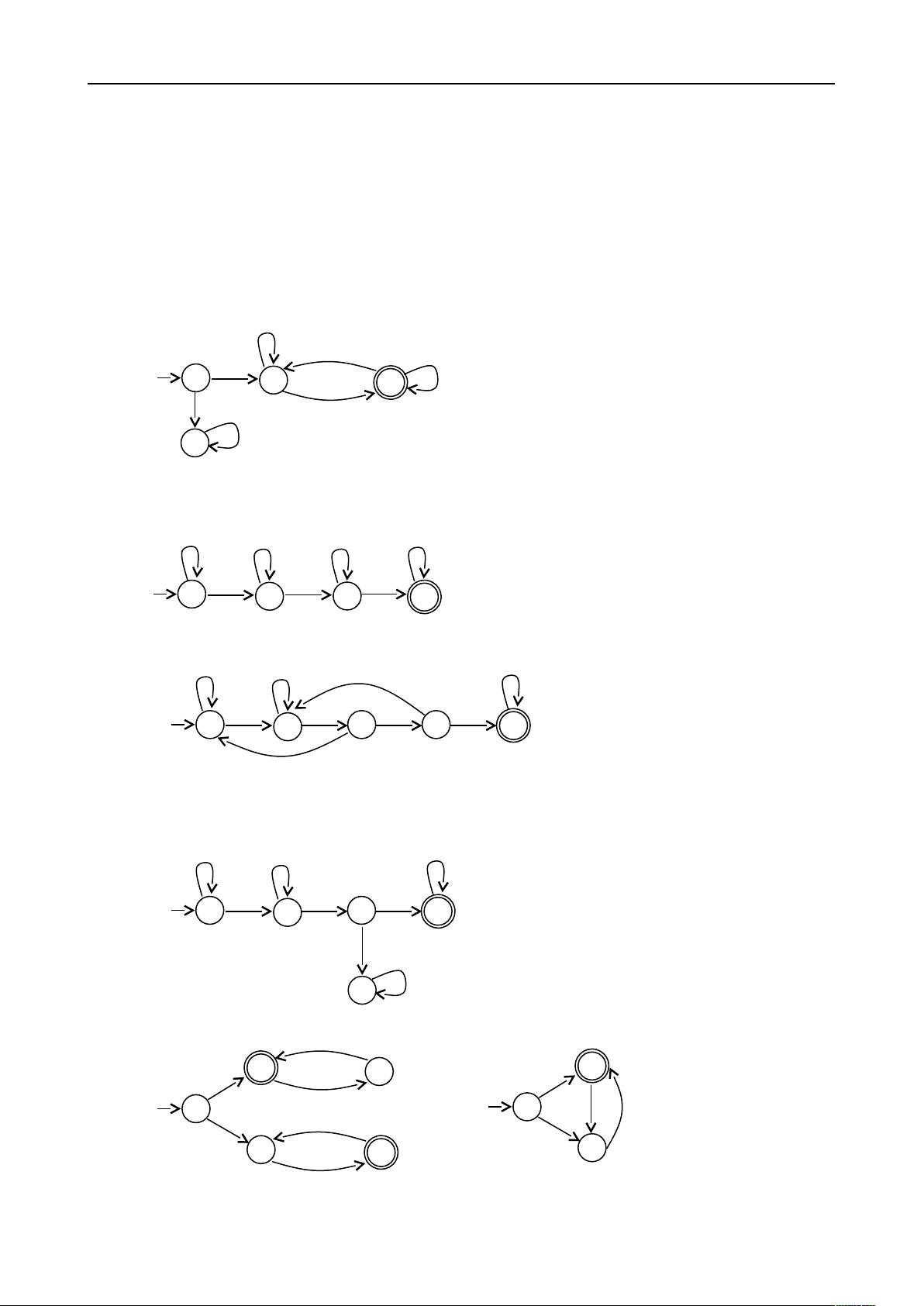
1.6 画出识别下述语言的 DFA 的状态图。
a){w | w 从 1 开始以 0 结束}
b){w | w 至少有 3 个 1}
c) {w | w 含有子串 0101}
d) {w | w 的长度不小于 3,且第三个符号为 0}
e) {w | w 从 0 开始且为奇长度,或从 1 开始且为偶长度}
或
- 2 -
0
0
1
1
1
0,1
0
0
1
0
0
1
1
0,1
0,1
1
0
0
1
1 0 1
0
0,1
0
0,1
0,1
1
1
0,1 0
0,1
0,1
0,1
0
0,1
1
0,1
0
0,1
1
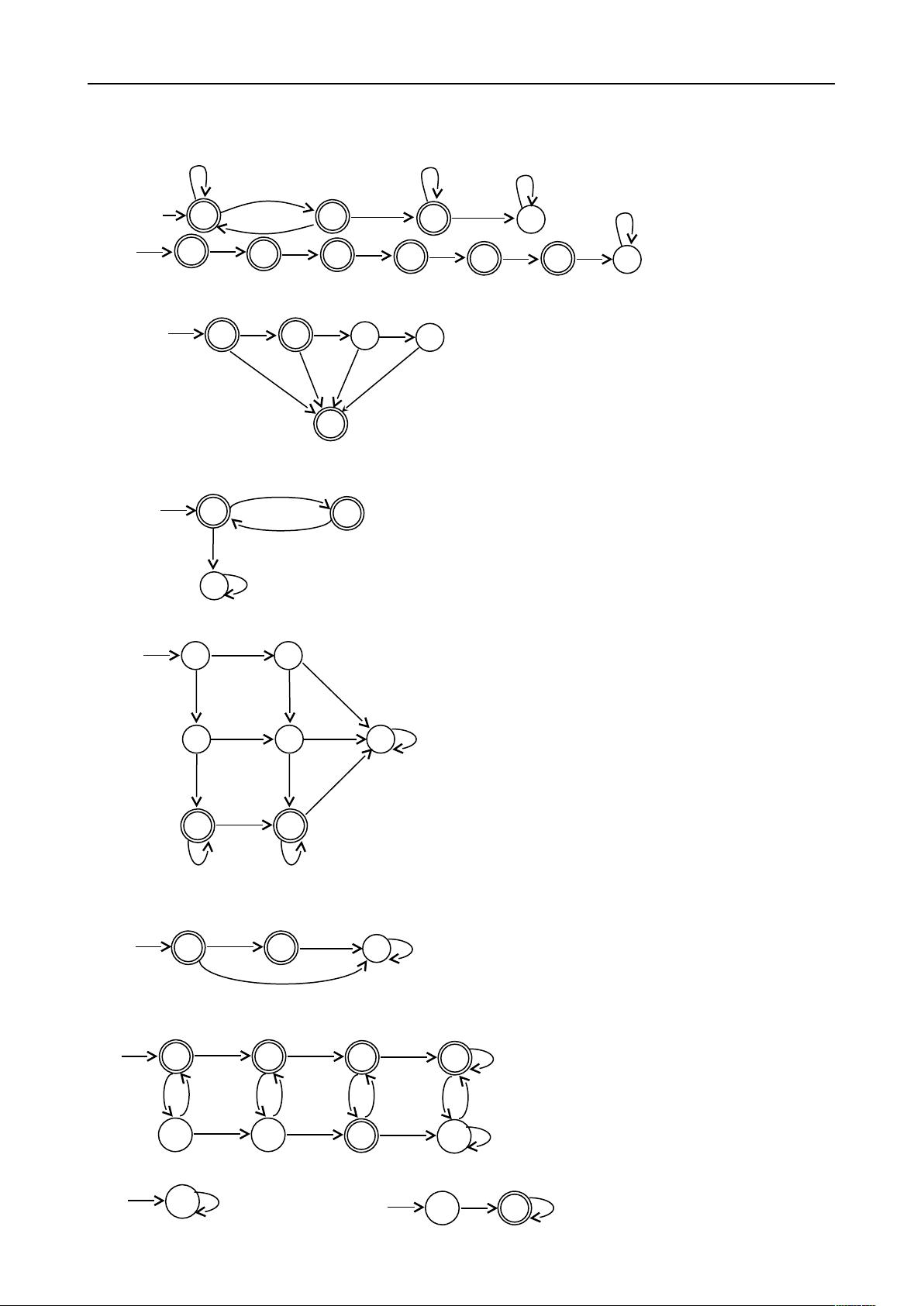
f) {w | w 不含子串 110}
g) {w | w 的长度不超过 5}
h){w | w 是除 11 和 111 以外的任何字符}
i){w | w 的奇位置均为 1}
j) {w | w 至少含有 2 个 0,且至多含有 1 个 1}
k) {ε,0}
l) {w | w 含有偶数个 0,或恰好两个 1}
m) 空集 n) 除空串外的所有字符串
- 3 -
0,1
0
1
0
1
1
0
0,1
0,1
0,1
0,1
0,1 0,1
0,1
1 1
1
0,1
0 0 0
0
0
1
0
0
1
1
1
1
1
0
0
0,1
0
0,1
0,1
1
1
0
0,1
0,1
1
1
0
0
1
1
1
1
1
0
0
0
0
0
0
1
0,1
0,1
0,1
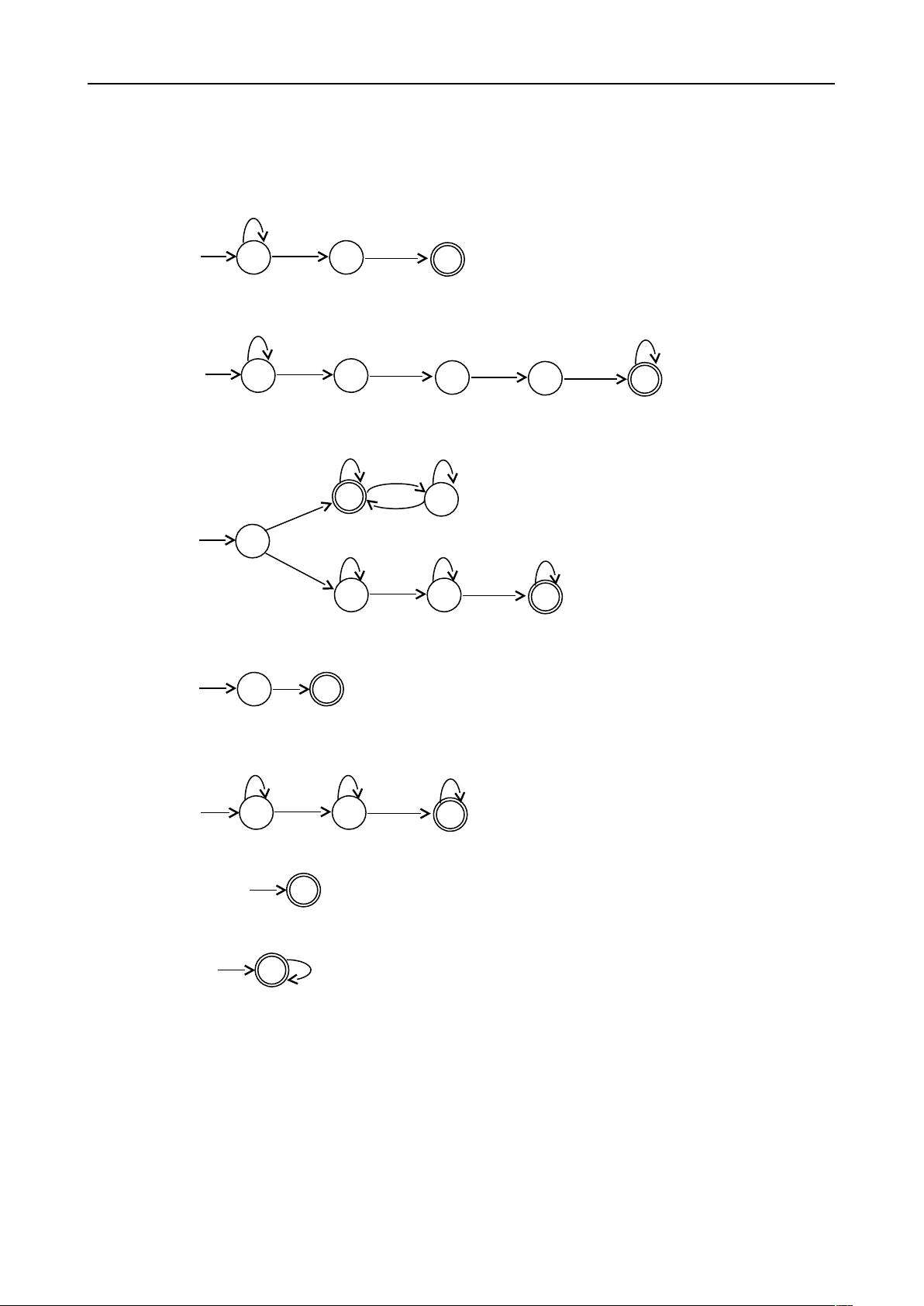
1.7 给出识别下述语言的 NFA,且要求符合规定的状态数。
a. {w | w 以 00 结束},三个状态
b. 语言{w | w 含有子串 0101,即对某个 x 和 y,w=x0101y},5 个状态.
c. 语言{w | w 含有偶数个 0 或恰好两个 1},6 个状态。
d. 语言{0},2 个状态。
e. 语言 0
*
1
*
0
*
0,3 个状态。
f. 语言{ε},1 个状态。
g. 语言 0
*
,1 个状态。
2.11 证明每一台 NFA 都能够转换成等价的只有一个接受状态的 NFA。
证明:设 NFA M={Q,Σ,δ,q
0
,F},F={r
i1
,……,
r
ik
}.添加一个状态 p 后,r
i1
,……,
r
ik
分别向 p 引 ε 箭头,将
r
i1
,……,
r
ik
变为非接受状态,p 变为接受状态。又因为添加 ε 箭头不影响 NFA 识别语言,所以命题成立。
2.14 a 证明:设 M 是一台语言 B 的 DFA,交换 M 的接状态与非接受状态得到一台新的 DFA,则这台新的
DFA 是识别 B 的补集,因此,正则语言类受在补运算下封闭。
b 举例说明:设 M 是一台识别语言 B 的 NFA,交换 M 的接受状态与非接受状态得到一台新的
NFA,这台新的 NFA 不一定识别 B 的补集。NFA 识别的语言类在补集下封闭吗?解释你的回答。
- 4 -
0
0
0,1
0
1
0,1
0
1
0,1
0
1
1
1
0
1
0 0
0
0
0
0 1
0
0
解:
a. M 是 DFA, M 是{Q,∑,δ,q
0
,F},令 N={Q,∑,δ,q
0
,Q-F},设 ω=ω
1
ω
2
…ω
n
是字母表上任意字符串,因为
M 与 N 均为 DFA,所以必然存在 Q 中状态序列 r
0
,r
1
,…,r
n
,使得:r
0
=q
0
, δ(r
i
, ω
i+1
)=r
i+1
, i=0,…,n-1
1)若 r
n
F 则 ωB;
2)若 r
n
F,则 r
n
Q-F,即 N 接受 ω,若 ωB,
所以 N 接受 B 的补集,即 B 的补集正则。
所以,正则语言类在补运算下封闭。
b. 设 B 为{0}。NFA M:
可识别它。
依题对它作变换,得到 N:
则 N 识别的语言{ε}不是 B 的子集。所以交换 M 的接受状态与非接受状态得到的新的 NFA 不一定
识别 B 的补集。
但是由于 NFA 识别的语言类与 DFA 识别的语言类相同,即正则语言类。由 a 的证明,正则语言类
在补运算封闭,可知,NFA 识别的语言类---正则语言类在补运算下封闭。
若 NFA 识别语言 A,必有 等价的 DFA 识别 A,从而由 a 知,可交换 DFA 的接受与非接受状态构造
识别 A 的补集的 DFA,则必有等价的 NFA 识别 A 的补集。只是,该 NFA 未必有原 NFA 交换接受与
非接受状态构造而成。
1.15 给 出 一 个 反 例 , 说 明 下 述 构 造 不 能 证 明 定 理 2.24 , 即 正 则 语 言 类 在 星 号 运 算 下 封 闭 。 设
N=(Q
1
,Σ,δ
1
,q
1
,F
1
)识别 A
1
。如下构造 N=(Q
1
,Σ,δ
1
,q
1
,F
1
)。 N 应该识别 A
1
*
。
a. N 的状态集是 N
1
的状态集。
b. N 的起始状态是 N
1
的起始状态相同。
c. F={q
1
}∪F
1
。F 的接受状态是原来的接受状态加上它的起始状态。
d. 定义 δ 如下:对每一个 q 属于 Q 和每一个 a 属于 Σ
。
解:设 N
1
识别语言 A={至少含有一个 1},其中输入字母表为{0,1},可知 A
*
={空串或至少含有一个
1}。
N
1
: N:
按上述规定构造 N 的状态图如上。可以看出 L(N)={0,1}
*
不等于 A
*
. 所以如此构造的 N 不一定识别 A
*
.
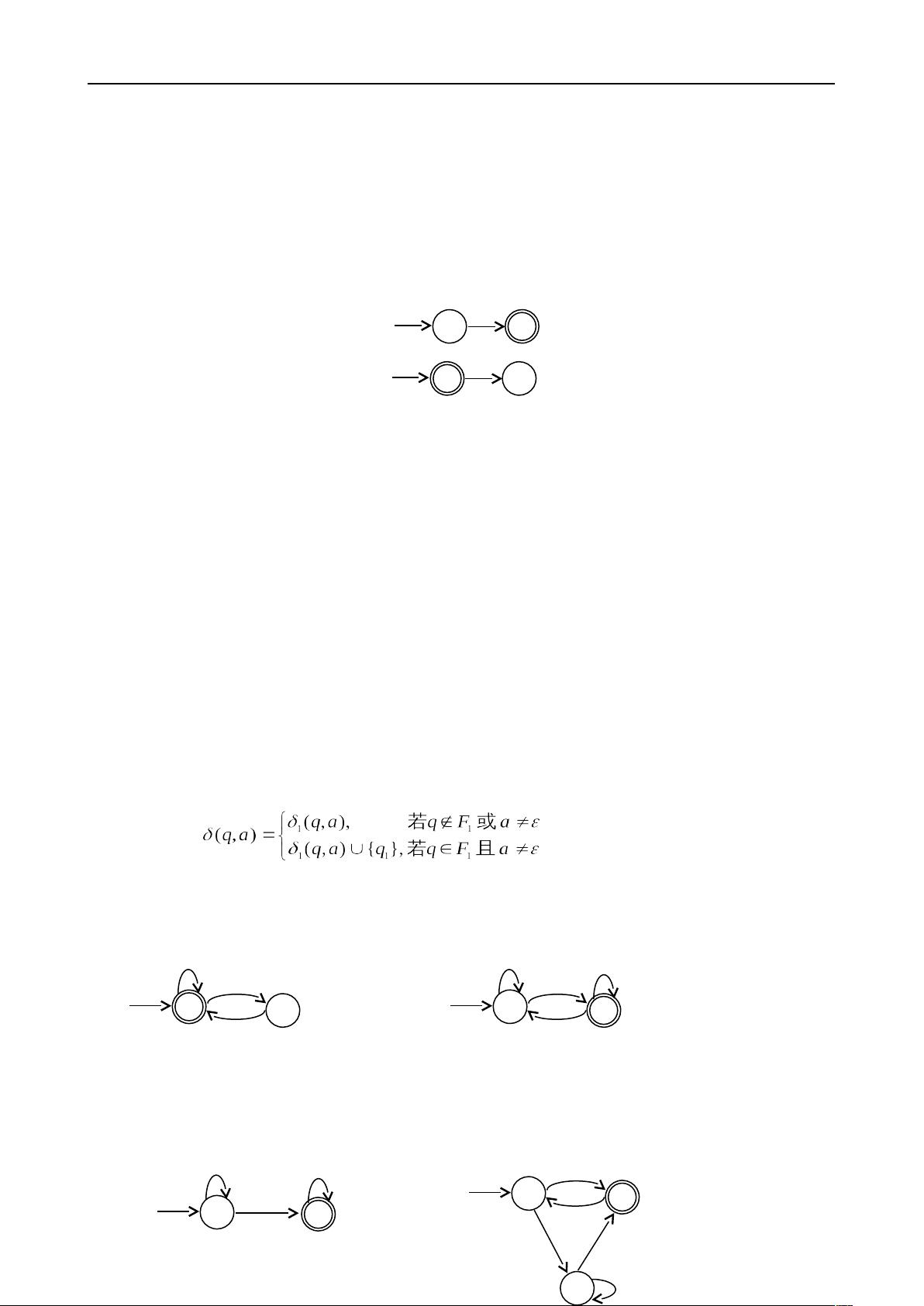
1.16 使用定理 2.19 中给出的构造,把下图中的两台非确定型有穷自动机转换成等价的确定型有穷自动机。
- 5 -
0
0
1
0,1
0,1
1
0,1
0,1
a,b
a
b
1
2
a
a,b
b
a
1
2
3
剩余43页未读,继续阅读
资源评论

Vermillion-
- 粉丝: 6
- 资源: 2
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功