一阶电路的方波响应是电路分析领域中一个基础且重要的主题,它涉及到电路中能量存储元件——电容器的充放电过程,以及电阻对电流的影响。通过研究一阶电路对方波信号的响应,我们不仅可以深入理解电路的基本概念和响应特性,还能掌握电路分析的一些基本技巧。一阶电路通常是指电路中只包含一个能量存储元件,即可以是电阻和电容(RC电路),也可以是电阻和电感(RL电路)的组合。在本篇教学方案中,我们将主要聚焦于RC电路的方波响应。
一阶电路的基本概念是指在电路中只有一个储能元件,如一个电容或一个电感。在RC电路中,电容器存储电荷,而电阻器限制电流的流动。电路的响应取决于电路的时间常数τ,这是由电路的电阻R和电容C值决定的。时间常数τ描述了电路由一种状态转变为另一种状态所需的时间。在电路的暂态分析中,τ是关键参数,它决定了电路响应的速率。
零状态响应是指电路的储能元件初始时没有存储能量,例如电容器未充电。当给定一个阶跃电压信号时,电路的响应完全由输入信号决定,没有受到任何初始条件的影响。零输入响应则相反,它发生在电路输入信号为零,但储能元件已经存储了能量时,此时电路的响应是由初始条件决定的。
理解零状态响应和零输入响应是电路分析的基础。这些概念帮助我们区分电路行为是由于外部激励引起的还是由于内部条件(如初始存储的能量)引起的。这对于分析电路的工作状态至关重要。
时间常数τ的测量是电路分析中的一个关键技能。τ可以通过理论公式τ=RC计算得到,其中R是电阻的阻值,C是电容的容值。在实验中,τ也可以通过观察电容器电压随时间的变化曲线来测量。当我们给RC电路施加阶跃电压时,电容器开始充电,其电压uc随时间的增加而指数增加,直到达到电源电压。通过测量电压达到电源电压63.2%的点(即1-1/e的点),我们可以确定时间常数τ。此过程中的衰减率(电压下降的速率)与时间常数有关,可以使用τ=n·Dx公式来计算,其中n是一个比例常数,Dx是电压波形的衰减率。
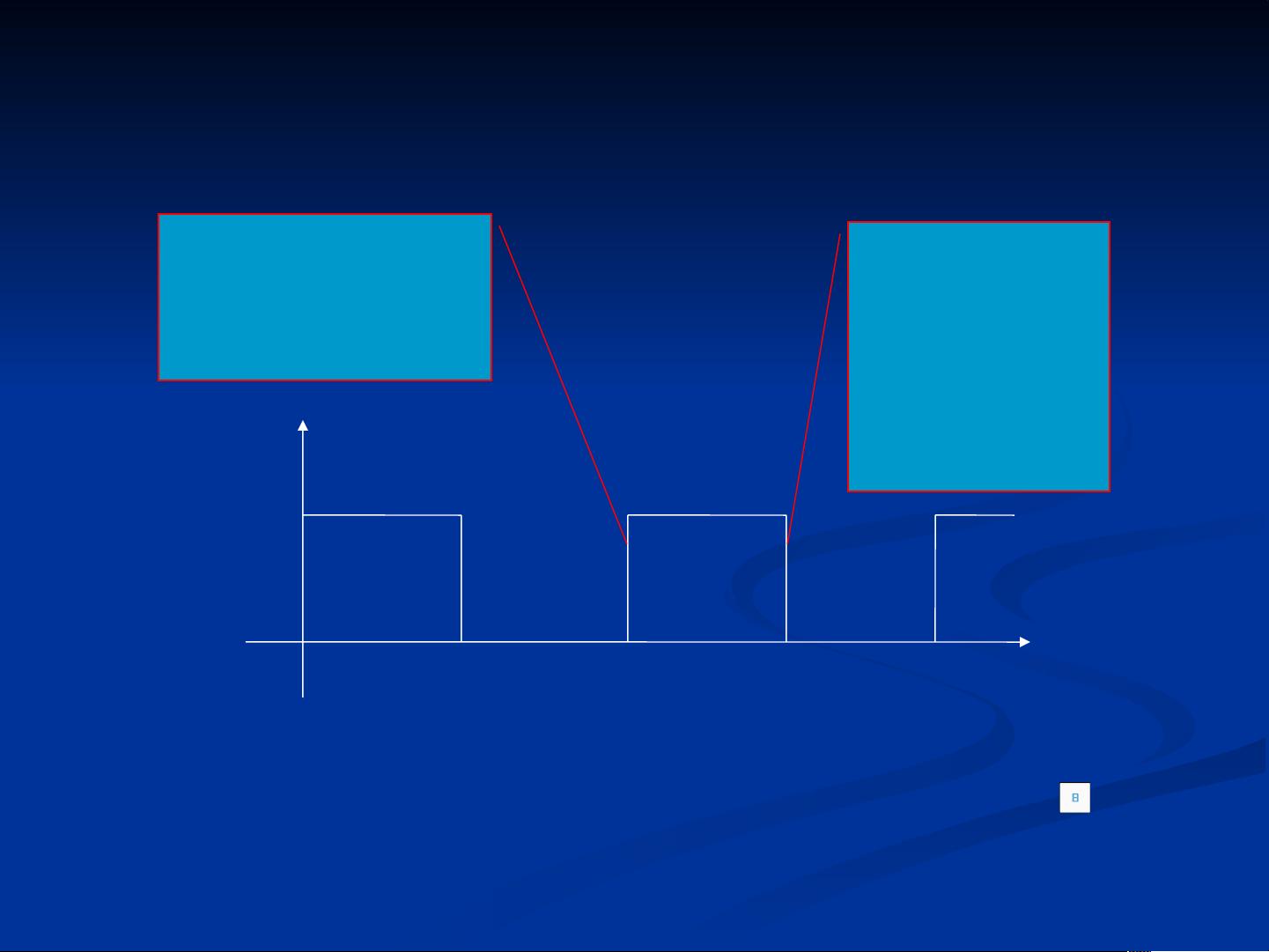
微分电路和积分电路是电路分析中经常使用的电路结构。微分电路可以将输入信号的时间变化率转换为输出电压,当输入信号为方波时,输出信号呈现为尖峰脉冲波形。积分电路则可以将输入信号的累积时间积分转换为输出电压,输入方波时,输出电压近似于一个三角波形,与输入信号的时间积分成正比。
在实验内容部分,学生需要进行一系列实验来观测一阶电路的行为。实验包括了观测RC电路的阶跃响应,以及微分电路和积分电路对方波输入信号的响应。学生必须画出电路电压uc波形图、电流i(t)波形图、微分电路输出电压uR波形图和积分电路电压uc波形图。同时,学生还需通过实验数据计算时间常数τ,并分析电阻R、电容C等参数的变化对时间常数τ的影响。
在实验过程中,还有一些重要的注意事项。为了确保实验结果的准确性,学生需要注意调整示波器的垂直灵敏度和水平灵敏度,并保持它们不变。这对于精确测量波形的变化和时间常数至关重要。
通过本教学方案,学生不仅能够掌握一阶电路的基本概念,理解零状态响应和零输入响应的区别,而且能够通过实验测量时间常数,并观察微分电路和积分电路的特性。这些知识和技能将帮助学生在电路分析和设计方面打下坚实的基础。