GAN生成对抗网络综述.pdf_gan实战pdf,gan网络综述资源-CSDN文库

需积分: 50 73 浏览量 2020-04-24 01:14:40 上传评论 3 收藏 1.99MB PDF 举报

资源推荐

资源详情

资源评论

JOURNAL OF L

X CLASS FILES, VOL. 14, NO. 8, AUGUST 2015 1

A Review on Generative Adversarial Networks:

Algorithms, Theory, and Applications

Jie Gui, Zhenan Sun, Yonggang Wen, Dacheng Tao, Jieping Ye

Abstract—Generative adversarial networks (GANs) are a hot research topic recently. GANs have been widely studied since 2014, and

a large number of algorithms have been proposed. However, there is few comprehensive study explaining the connections among

different GANs variants, and how they have evolved. In this paper, we attempt to provide a review on various GANs methods from the

perspectives of algorithms, theory, and applications. Firstly, the motivations, mathematical representations, and structure of most GANs

algorithms are introduced in details. Furthermore, GANs have been combined with other machine learning algorithms for speciﬁc

applications, such as semi-supervised learning, transfer learning, and reinforcement learning. This paper compares the commonalities

and differences of these GANs methods. Secondly, theoretical issues related to GANs are investigated. Thirdly, typical applications of

GANs in image processing and computer vision, natural language processing, music, speech and audio, medical ﬁeld, and data

science are illustrated. Finally, the future open research problems for GANs are pointed out.

Index Terms—Deep Learning, Generative Adversarial Networks, Algorithm, Theory, Applications.

1 INTRODUCTION

ENERATIVE adversarial networks (GANs) have become

a hot research topic recently. Yann LeCun, a legend in

deep learning, said in a Quora post “GANs are the most

interesting idea in the last 10 years in machine learning.”

There are a large number of papers related to GANs accord-

ing to Google scholar. For example, there are about 11,800

papers related to GANs in 2018. That is to say, there are

about 32 papers everyday and more than one paper every

hour related to GANs in 2018.

GANs consist of two models: a generator and a dis-

criminator. These two models are typically implemented by

neural networks, but they can be implemented with any

form of differentiable system that maps data from one space

to the other. The generator tries to capture the distribution

of true examples for new data example generation. The

discriminator is usually a binary classiﬁer, discriminating

generated examples from the true examples as accurately

as possible. The optimization of GANs is a minimax opti-

mization problem. The optimization terminates at a saddle

point that is a minimum with respect to the generator and

a maximum with respect to the discriminator. That is, the

optimization goal is to reach Nash equilibrium [1]. Then,

the generator can be thought to have captured the real

distribution of true examples.

Some previous work has adopted the concept of making

two neural networks compete with each other. The most

J. Gui is with the Department of Computational Medicine and Bioinformatics,

University of Michigan, USA (e-mail: guijie@ustc.edu).

Z. Sun is with the Center for Research on Intelligent Perception and

Computing, Chinese Academy of Sciences, Beijing 100190, China (e-mail:

znsun@nlpr.ia.ac.cn).

Y. Wen is with the School of Computer Science and Engineering, Nanyang

Technological University, Singapore 639798 (e-mail: ygwen@ntu.edu.sg).

D. Tao is with the UBTECH Sydney Artiﬁcial Intelligence Center and

the School of Information Technologies, the Faculty of Engineering and

Information Technologies, the University of Sydney, Australia. (e-mail:

Dacheng.Tao@Sydney.edu.au).

J. Ye is with DiDi AI Labs, P.R. China and University of Michigan, Ann

Arbor.(e-mail:jpye@umich.edu).

relevant work is predictability minimization [2]. The connec-

tions between predictability minimization and GANs can be

found in [3], [4].

The popularity and importance of GANs have led to sev-

eral previous reviews. The difference from previous work is

summarized in the following.

1) GANs for speciﬁc applications: There are surveys of

using GANs for speciﬁc applications such as image

synthesis and editing [5], audio enhancement and

synthesis [6].

2) General survey: The earliest relevant review was

probably the paper by Wang et al. [7] which mainly

introduced the progress of GANs before 2017. Ref-

erences [8], [9] mainly introduced the progress of

GANs prior to 2018. The reference [10] introduced

the architecture-variants and loss-variants of GANs

only related to computer vision. Other related work

can be found in [11]–[13].

As far as we know, this paper is the ﬁrst to provide a

comprehensive survey on GANs from the algorithm, theory,

and application perspectives which introduces the latest

progress. Furthermore, our paper focuses on applications

not only to image processing and computer vision, but also

sequential data such as natural language processing, and

other related areas such as medical ﬁeld.

The remainder of this paper is organized as follows: The

related work is discussed in Section 2. Sections 3-5 introduce

GANs from the algorithm, theory, and applications perspec-

tives, respectively. Tables 1 and 2 show GANs’ algorithms

and applications which will be discussed in Sections 3 and

5, respectively. The open research problems are discussed in

Section 6 and Section 7 concludes the survey.

2 RELATED WORK

GANs belong to generative algorithms. Generative algo-

rithms and discriminative algorithms are two categories of

arXiv:2001.06937v1 [cs.LG] 20 Jan 2020

JOURNAL OF L

X CLASS FILES, VOL. 14, NO. 8, AUGUST 2015 2

TABLE 1: A overview of GANs’ algorithms discussed in Section 3

GANs’ Representative variants InfoGAN [14], cGANs [15], CycleGAN [16], f -GAN [17], WGAN [18], WGAN-GP [19],

LS-GAN [20]

Objective function LSGANs [21], [22], hinge loss based GAN [23]–[25], MDGAN [26], unrolled GAN [27],

SN-GANs [23], RGANs [28]

Skills ImprovedGANs [29], AC-GAN [30]

LAPGAN [31], DCGANs [32], PGGAN [33], StackedGAN [34], SAGAN [35], BigGANs [36],

GANs training StyleGAN [37], hybrids of autoencoders and GANs (EBGAN [38],

Structure BEGAN [39], BiGAN [40]/ALI [41], AGE [42]),

multi-discriminator learning (D2GAN [43], GMAN [44]),

multi-generator learning (MGAN [45], MAD-GAN [46]),

multi-GAN learning (CoGAN [47])

Semi-supervised learning CatGANs [48], feature matching GANs [29], VAT [49], ∆-GAN [50], Triple-GAN [51]

DANN [52], CycleGAN [53], DiscoGAN [54], DualGAN [55], StarGAN [56],

Task driven GANs Transfer learning CyCADA [57], ADDA [58], [59], FCAN [60],

unsupervised pixel-level domain adaptation (PixelDA) [61]

Reinforcement learning GAIL [62]

TABLE 2: Applications of GANs discussed in Section 5

Field Subﬁeld Method

Super-resolution SRGAN [63], ESRGAN [64], Cycle-in-Cycle GANs [65],

SRDGAN [66], TGAN [67]

DR-GAN [68], TP-GAN [69], PG

[70], PSGAN [71],

Image synthesis and manipulation APDrawingGAN [72], IGAN [73],

Image processing and computer vision introspective adversarial networks [74], GauGAN [75]

Texture synthesis MGAN [76], SGAN [77], PSGAN [78]

Object detection Segan [79], perceptual GAN [80], MTGAN [81]

Video VGAN [82], DRNET [83], Pose-GAN [84], video2video [85],

MoCoGan [86]

Natural language processing (NLP) RankGAN [87], IRGAN [88], [89], TAC-GAN [90]

Sequential data Music RNN-GAN (C-RNN-GAN) [91], ORGAN [92],

SeqGAN [93], [94]

machine learning algorithms. If a machine learning algo-

rithm is based on a fully probabilistic model of the observed

data, this algorithm is generative. Generative algorithms

have become more popular and important due to their wide

practical applications.

2.1 Generative algorithms

Generative algorithms can be classiﬁed into two classes:

explicit density model and implicit density model.

2.1.1 Explicit density model

An explicit density model assumes the distribution and

utilizes true data to train the model containing the distri-

bution or ﬁt the distribution parameters. When ﬁnished,

new examples are produced utilizing the learned model or

distribution. The explicit density models include maximum

likelihood estimation (MLE), approximate inference [95],

[96], and Markov chain method [97]–[99]. These explicit

density models have an explicit distribution, but have lim-

itations. For instance, MLE is conducted on true data and

the parameters are updated directly based on the true data,

which leads to an overly smooth generative model. The gen-

erative model learned by approximate inference can only

approach the lower bound of the objective function rather

than directly approach the objective function, because of

the difﬁculty in solving the objective function. The Markov

chain algorithm can be used to train generative models, but

it is computationally expensive. Furthermore, the explicit

density model has the problem of computational tractability.

It may fail to represent the complexity of true data distribu-

tion and learn the high-dimensional data distributions [100].

2.1.2 Implicit density model

An implicit density model does not directly estimate or

ﬁt the data distribution. It produces data instances from

the distribution without an explicit hypothesis [101] and

utilizes the produced examples to modify the model. Prior

to GANs, the implicit density model generally needs to be

trained utilizing either ancestral sampling [102] or Markov

chain-based sampling, which is inefﬁcient and limits their

practical applications. GANs belong to the directed implicit

density model category. A detailed summary and relevant

papers can be found in [103].

2.1.3 The comparison between GANs and other generative

algorithms

GANs were proposed to overcome the disadvantages of

other generative algorithms. The basic idea behind adver-

sarial learning is that the generator tries to create as real-

istic examples as possible to deceive the discriminator. The

discriminator tries to distinguish fake examples from true

examples. Both the generator and discriminator improve

through adversarial learning. This adversarial process gives

GANs notable advantages over other generative algorithms.

More speciﬁcally, GANs have advantages over other gener-

ative algorithms as follows:

1) GANs can parallelize the generation, which is im-

possible for other generative algorithms such as

JOURNAL OF L

X CLASS FILES, VOL. 14, NO. 8, AUGUST 2015 3

PixelCNN [104] and fully visible belief networks

(FVBNs) [105], [106].

2) The generator design has few restrictions.

3) GANs are subjectively thought to produce better

examples than other methods.

Refer to [103] for more detailed discussions about this.

2.2 Adversarial idea

The adversarial idea has been successfully applied to many

areas such as machine learning, artiﬁcial intelligence, com-

puter vision and natural language processing. The recent

event that AlphaGo [107] defeats world’s top human player

engages public interest in artiﬁcial intelligence. The interme-

diate version of AlphaGo utilizes two networks competing

with each other.

Adversarial examples [108]–[117] have the adversarial

idea, too. Adversarial examples are those examples which

are very different from the real examples, but are classiﬁed

into a real category very conﬁdently, or those that are

slightly different than the real examples, but are classiﬁed

into a wrong category. This is a very hot research topic

recently [112], [113]. To be against adversarial attacks [118],

[119], references [120], [121] utilize GANs to conduct the

right defense.

Adversarial machine learning [122] is a minimax prob-

lem. The defender, who builds the classiﬁer that we want

to work correctly, is searching over the parameter space to

ﬁnd the parameters that reduce the cost of the classiﬁer as

much as possible. Simultaneously, the attacker is searching

over the inputs of the model to maximize the cost.

The adversarial idea exists in adversarial networks, ad-

versarial learning, and adversarial examples. However, they

have different objectives.

3 ALGORITHMS

In this section, we ﬁrst introduce the original GANs. Then,

the representative variants, training, evaluation of GANs,

and task-driven GANs are introduced.

3.1 Generative Adversarial Nets (GANs)

The GANs framework is straightforward to implement

when the models are both neural networks. In order to learn

the generator’s distribution p

over data x, a prior on input

noise variables is deﬁned as p

(z) [3] and z is the noise vari-

able. Then, GANs represent a mapping from noise space to

data space as G (z, θ

), where G is a differentiable function

represented by a neural network with parameters θ

. Other

than G, the other neural network D (x, θ

) is also deﬁned

with parameters θ

and the output of D (x) is a single scalar.

D (x) denotes the probability that x was from the data

rather than the generator G. The discriminator D is trained

to maximize the probability of giving the correct label to

both training data and fake samples generated from the

generator G. G is trained to minimize log (1 − D (G (z)))

simultaneously .

3.1.1 Objective function

Different objective functions can be used in GANs.

3.1.1.1 Original minimax game:

The objective function of GANs [3] is

min

max

V (D, G) = E

x∼p

data

(x)

[log D (x)]

z∼p

(z)

[log (1 − D (G (z)))] .

(1)

log D (x) is the cross-entropy between [1 0]

and

[D (x) 1 − D (x)]

. Similarly, log (1 − D (G (z)))

is the cross-entropy between [0 1]

and

[D (G (z)) 1 − D (G (z))]

. For ﬁxed G, the optimal

discriminator D is given by [3]:

∗

(x) =

data

(x)

data

(x) + p

(x)

. (2)

The minmax game in (1) can be reformulated as:

C(G) = max

V (D, G)

= E

x∼p

data

[log D

∗

(x)]

z∼p

[log (1 − D

∗

(G (z)))]

= E

x∼p

data

[log D

∗

(x)] + E

x∼p

[log (1 − D

∗

(x))]

= E

x∼p

data

log

data

(x)

data

(x)+p

(x))

x∼p

(x)

data

(x)+p

(x))

− 2 log 2.

(3)

The deﬁnition of KullbackLeibler (KL) divergence and

Jensen-Shannon (JS) divergence between two probabilistic

distributions p (x) and q (x) are deﬁned as

KL( pk q) =

p (x) log

p (x)

q (x)

dx, (4)

JS(pk q) =

KL( pk

p + q

) +

KL( qk

p + q

). (5)

Therefore, (3) is equal to

C(G) = KL( p

data

) + KL( p

data

)

−2 log 2

= 2JS(p

data

k p

) − 2 log 2.

(6)

Thus, the objective function of GANs is related to both KL

divergence and JS divergence.

3.1.1.2 Non-saturating game:

It is possible that the Equation (1) cannot provide sufﬁcient

gradient for G to learn well in practice. Generally speak-

ing, G is poor in early learning and samples are clearly

different from the training data. Therefore, D can reject the

generated samples with high conﬁdence. In this situation,

log (1 − D (G (z))) saturates. We can train G to maximize

log (D (G (z))) rather than minimize log (1 − D (G (z))).

The cost for the generator then becomes

(G)

= E

z∼p

(z)

[− log (D (G (z)))]

= E

x∼p

[− log (D (x))] .

(7)

This new objective function results in the same ﬁxed point

of the dynamics of D and G but provides much larger

gradients early in learning. The non-saturating game is

heuristic, not being motivated by theory. However, the

non-saturating game has other problems such as unstable

numerical gradient for training G. With optimal D

∗

, we

have

x∼p

[− log (D

∗

(x))] + E

x∼p

[log (1 − D

∗

(x))]

= E

x∼p

log

(1−D

∗

(x))

∗

(x)

= E

x∼p

log

(x)

data

(x)

= KL( p

k p

data

(8)

JOURNAL OF L

X CLASS FILES, VOL. 14, NO. 8, AUGUST 2015 4

Therefore, E

x∼p

[− log (D

∗

(x))] is equal to

x∼p

[− log (D

∗

(x))]

= KL( p

k p

data

) − E

x∼p

[log (1 − D

∗

(x))] .

(9)

From (3) and (6), we have

x∼p

data

[log D

∗

(x)] + E

x∼p

[log (1 − D

∗

(x))]

= 2JS(p

data

k p

) − 2 log 2.

(10)

Therefore, E

x∼p

[log (1 − D

∗

(x))] equals

x∼p

[log (1 − D

∗

(x))]

= 2JS(p

data

k p

) − 2 log 2 − E

x∼p

data

[log D

∗

(x)] .

(11)

By substituting (11) into (9), (9) reduces to

x∼p

[− log (D

∗

(x))]

= KL( p

k p

data

) − 2JS(p

data

k p

x∼p

data

[log D

∗

(x)] + 2 log 2.

(12)

From (12), we can see that the optimization of the alternative

G loss in the non-saturating game is contradictory because

the ﬁrst term aims to make the divergence between the

generated distribution and the real distribution as small as

possible while the second term aims to make the divergence

between these two distributions as large as possible due

to the negative sign. This will bring unstable numerical

gradient for training G. Furthermore, KL divergence is not a

symmetrical quantity, which is reﬂected from the following

two examples

• If p

data

(x) → 0 and p

(x) → 1, we have

KL( p

k p

data

) → +∞.

• If p

data

(x) → 1 and p

(x) → 0, we have

KL( p

k p

data

) → 0.

The penalizations for two errors made by G are completely

different. The ﬁrst error is that G produces implausible sam-

ples and the penalization is rather large. The second error is

that G does not produce real samples and the penalization is

quite small. The ﬁrst error is that the generated samples are

inaccurate while the second error is that generated samples

are not diverse enough. Based on this, G prefers producing

repeated but safe samples rather than taking risk to produce

different but unsafe samples, which has the mode collapse

problem.

3.1.1.3 Maximum likelihood game:

There are many methods to approximate (1) in GANs.

Under the assumption that the discriminator is optimal,

minimizing

(G)

= E

z∼p

(z)



− exp



−1

(D (G (z)))



= E

z∼p

(z)

[−D (G (z))/(1 − D (G (z)))] ,

(13)

where σ is the logistic sigmoid function, equals minimiz-

ing (1) [123]. The demonstration of this equivalence can

be found in Section 8.3 of [103]. Furthermore, there are

other possible ways of approximating maximum likelihood

within the GANs framework [17]. A comparison of original

zero-sum game, non-saturating game, and maximum likeli-

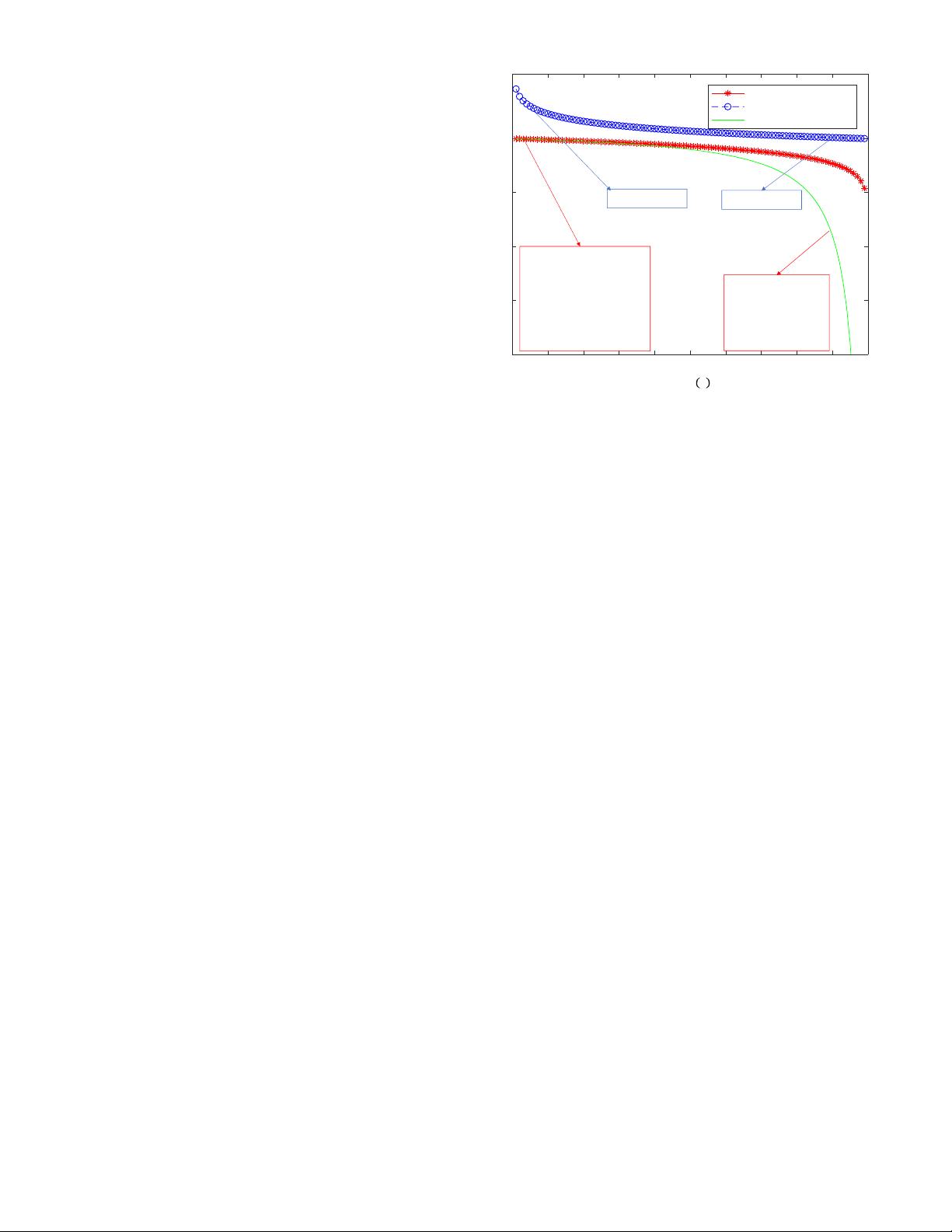
hood game is shown in Fig. 1.

Three observations can be obtained from Fig. 1.

• First, when the sample is possible to be fake, that is

on the left end of the ﬁgure, both the maximum like-

lihood game and the original minimax game suffer

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

-20

-15

-10

-5

Original

Non-saturating

Maximum likelihood cost

When samples are

possible to be fake, we

want to learn it to

improve the generator.

However, gradient in

this region is almost

vanishing

Gradient is

dominated by the

region where

samples in very

good quality.

High gradient

Low gradient

( )

Fig. 1: The three curves of “Original”, “Non-saturating”, and

“Maximum likelihood cost” denotes log (1 − D (G (z))),

− log (D (G (z))), and −D(G(z))/(1 − D(G(z))) in (1), (7),

and (13), respectively. The cost that the generator has for

generating a sample G(z) is only decided by the discrimi-

nator’s response to that generated sample. The larger prob-

ability the discriminator gives the real label to the generated

sample, the less cost the generator gets. This ﬁgure is repro-

duced from [103], [123].

from gradient vanishing. The heuristically motivated

non-saturating game does not have this problem.

• Second, maximum likelihood game also has the

problem that almost all of the gradient is from the

right end of the curve, which means that a rather

small number of samples in each minibatch dominate

the gradient computation. This demonstrates that

variance reduction methods could be an important

research direction for improving the performance of

GANs based on maximum likelihood game.

• Third, the heuristically motivated non-saturating

game has lower sample variance, which is the pos-

sible reason that it is more successful in real applica-

tions.

GAN Lab [124] is proposed as the interactive visualization

tool designed for non-experts to learn and experiment with

GANs. Bau et al. [125] present an analytic framework to

visualize and understand GANs.

3.2 GANs’ representative variants

There are many papers related to GANs [126]–[131] such as

CSGAN [132] and LOGAN [133]. In this subsection, we will

introduce GANs’ representative variants.

3.2.1 InfoGAN

Rather than utilizing a single unstructured noise vector z,

InfoGAN [14] proposes to decompose the input noise vector

into two parts: z, which is seen as incompressible noise; c,

which is called the latent code and will target the signiﬁcant

JOURNAL OF L

X CLASS FILES, VOL. 14, NO. 8, AUGUST 2015 5

structured semantic features of the real data distribution.

InfoGAN [14] aims to solve

min

max

(D, G) = V (D, G) − λI(c; G(z, c)), (14)

where V (D, G) is the objective function of original GAN,

G(z, c) is the generated sample, I is the mutual information,

and λ is the tunable regularization parameter. Maximizing

I(c; G(z, c)) means maximizing the mutual information be-

tween c and G(z, c) to make c contain as much important

and meaningful features of the real samples as possible.

However, I(c; G(z, c)) is difﬁcult to optimize directly in

practice since it requires access to the posterior P (c|x).

Fortunately, we can have a lower bound of I(c; G(z, c))

by deﬁning an auxiliary distribution Q(c|x) to approximate

P (c|x). The ﬁnal objective function of InfoGAN [14] is

min

max

(D, G) = V (D, G) − λL

(c; Q), (15)

where L

(c; Q) is the lower bound of I(c; G(z, c)). InfoGAN

has several variants such as causal InfoGAN [134] and semi-

supervised InfoGAN (ss-InfoGAN) [135].

3.2.2 Conditional GANs (cGANs)

GANs can be extended to a conditional model if both the

discriminator and generator are conditioned on some extra

information y. The objective function of conditional GANs

[15] is:

min

max

V (D, G) = E

x∼p

data

(x)

[log D ( x| y)]

z∼p

(z)

[log (1 − D (G ( z| y)))] .

(16)

By comparing (15) and (16), we can see that the generator

of InfoGAN is similar to that of cGANs. However, the latent

code c of InfoGAN is not known, and it is discovered by

training. Furthermore, InfoGAN has an additional network

Q to output the conditional variables Q(c|x).

Based on cGANs, we can generate samples conditioning

on class labels [30], [136], text [34], [137], [138], bounding

box and keypoints [139]. In [34], [140], text to photo-realistic

image synthesis is conducted with stacked generative ad-

versarial networks (SGAN) [141]. cGANs have been used

for convolutional face generation [142], face aging [143],

image translation [144], synthesizing outdoor images having

speciﬁc scenery attributes [145], natural image description

[146], and 3D-aware scene manipulation [147]. Chrysos et

al. [148] proposed robust cGANs. Thekumparampil et al.

[149] discussed the robustness of conditional GANs to noisy

labels. Conditional CycleGAN [16] uses cGANs with cyclic

consistency. Mode seeking GANs (MSGANs) [150] proposes

a simple yet effective regularization term to address the

mode collapse issue for cGANs.

The discriminator of original GANs [3] is trained to

maximize the log-likelihood that it assigns to the correct

source [30]:

L = E [log P (S = real| X

real

)]

+E [log (P (S = fake| X

fake

))] ,

(17)

which is equal to (1). The objective function of the auxiliary

classiﬁer GAN (AC-GAN) [30] has two parts: the loglikeli-

hood of the correct source, L

, and the loglikelihood of the

G(y)

fake

real

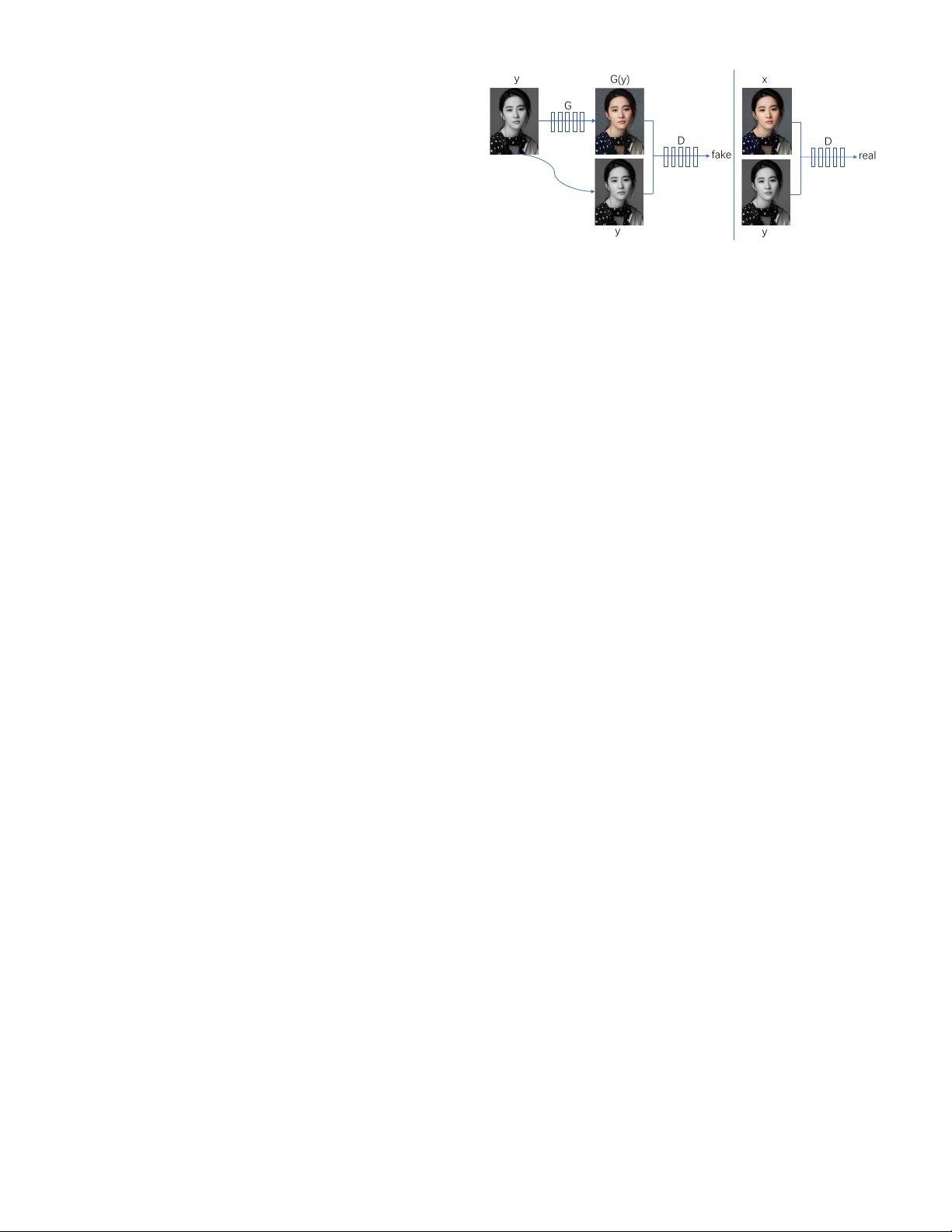
Fig. 2: Illustration of pix2pix: Training a conditional GANs

to map grayscale→color. The discriminator D learns to

classify between real grayscale, color tuples and fake (syn-

thesized by the generator). The generator G learns to fool

the discriminator. Different from the original GANs, both

the generator and discriminator observe the input grayscale

image and there is no noise input for the generator of

pix2pix.

correct class label, L

. L

is equivalent to L in (17). L

deﬁned as

= E [log P (C = c| X

real

)]

+E [log (P (C = c| X

fake

))] .

(18)

The discriminator and generator of AC-GAN is to maximize

+ L

and L

− L

, respectively. AC-GAN was the

ﬁrst variant of GANs that was able to produce recognizable

examples of all the ImageNet [151] classes.

Discriminators of most cGANs based methods [31], [41],

[152]–[154] feed conditional information y into the discrimi-

nator by simply concatenating (embedded) y to the input or

to the feature vector at some middle layer. cGANs with pro-

jection discriminator [155] adopts an inner product between

the condition vector y and the feature vector.

Isola et al. [156] used cGANs and sparse regularization

for image-to-image translation. The corresponding software

is called pix2pix. In GANs, the generator learns a mapping

from random noise z to G (z). In contrast, there is no noise

input in the generator of pix2pix. A novelty of pix2pix is

that the generator of pix2pix learns a mapping from an

observed image y to output image G (y), for example, from

a grayscale image to a color image. The objective of cGANs

in [156] can be expressed as

cGANs

(D, G) = E

x,y

[log D (x, y)]

[log (1 − D (y, G (y)))] .

(19)

Furthermore, l

distance is used:

(G) = E

x,y

[kx − G(y)k

] . (20)

The ﬁnal objective of [156] is

cGANs

(D, G) + λL

(G) , (21)

where λ is the free parameter. As a follow-up to pix2pix,

pix2pixHD [157] used cGANs and feature matching loss for

high-resolution image synthesis and semantic manipulation.

With the discriminators, the learning problem is a multi-task

learning problem:

min

max

k=1,2,3

GAN

(G, D

). (22)

剩余27页未读，继续阅读

评论收藏

内容反馈

qq_36225236

粉丝: 0
资源: 23

GAN生成对抗网络综述.pdf

【ch13-生成对抗网络】 GAN实战.pdf

生成对抗网络(GAN).pdf

生成对抗网络研究综述

《GANs生成式对抗网络综述：算法、理论与应用》【密歇根大学28页综述论文】.zip

GAN-生成式对抗网络

生成对抗网络GAN（ Generative Adversarial Networks）63PPT，GAN原理，介绍，变体详细

深度学习项目开发实战_生成对抗网络_编程案例解析实例详解课程教程.pdf

最新《生成式对抗网络GAN进展》综述论文

生成对抗网络原理及典型模型介绍.pptx

出自陶大程、叶杰平老师等大牛之手的 GAN 详细综述.rar

生成式对抗网络GAN综述

生成对抗网络综述：算法、理论与应用.rar

最新《生成式对抗网络》技术综述

深度学习-对抗生成网络实战(GAN).rar

对抗生成网络详细教程GAN.pptx

生成式对抗网络研究综述（2020年05月最新版本）

GAN生成对抗网络入门与实战视频教程

GAN对抗生成网络作者讲义

深度学习-对抗生成网络实战(GAN)视频课程

GAN生成对抗网络实战(PyTorch版)

生成式对抗网络GAN的研究进展与展望_王坤峰.pdf

GAN生成对抗网络入门与实战

对抗生成网络：从理解到实践

生成对抗网络wgan.py

李宏毅 -生成对抗网络GAN课件 234页

李宏毅GAN对抗生成网络2018最新ppt全套

生成对抗网络的详细介绍PPT

Python-GAN实战对抗生成网络深度学习随书代码

YOLOv8-deepsort 实现智能车辆目标检测+车辆跟踪+车辆计数

Transformer模型实现长期预测并可视化结果（附代码+数据集+原理介绍）

最新资源