数学规划模型.ppt.zip

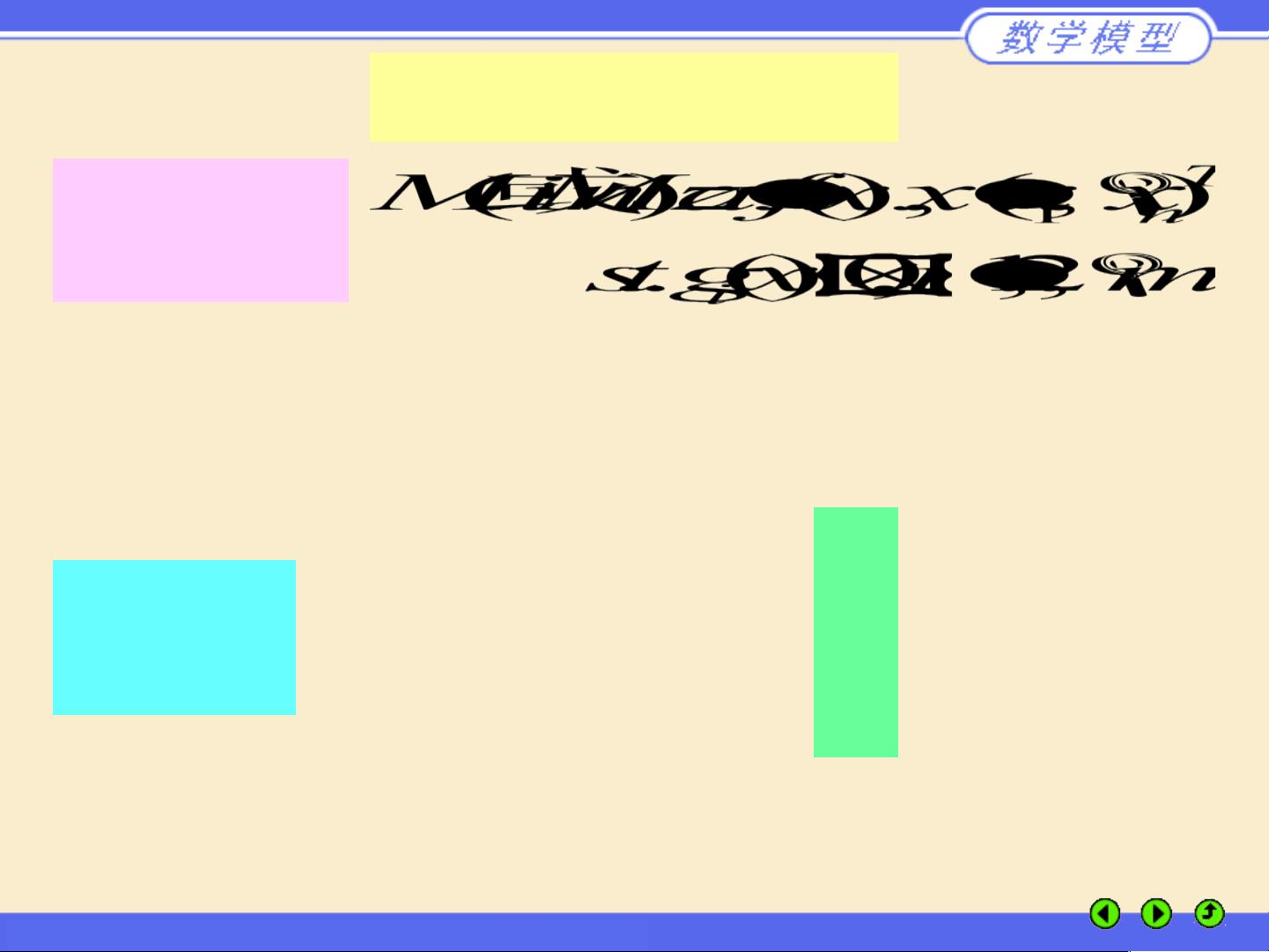
《数学规划模型》 在信息技术领域，数学规划模型是一种强大的工具，它被广泛应用于优化问题的解决，尤其是在数据科学、机器学习和运筹学中。本资料“数学规划模型.ppt.zip”提供了一个深入理解这一概念的机会，让我们一同探讨这个主题。 数学规划是通过建立数学模型来描述一个优化问题，并寻求最佳解决方案的过程。它分为线性规划、整数规划、非线性规划等不同类型，每种类型都有其特定的应用场景和解决策略。 1. **线性规划**：是最基础的数学规划形式，目标函数和约束条件都是线性的。例如，在资源分配、生产计划等问题中，线性规划可以找到最优的分配方案，使得总收益最大化或成本最小化。 2. **整数规划**：在实际问题中，决策变量往往不能取连续值，而是整数或二元（0/1）取值。整数规划是在线性规划的基础上加入整数约束，通常比线性规划更难求解，但能更准确地反映实际情况。 3. **非线性规划**：目标函数或约束条件包含非线性项，如平方、指数、对数等。非线性规划广泛应用于工程设计、经济预测等领域，解决更为复杂的问题。 4. **动态规划**：不同于以上规划方法，动态规划是处理具有时间序列性质问题的有效手段。它通过分解问题为子问题，然后逐个求解，最后组合成全局最优解。 5. **混合整数规划**：结合了整数和连续变量，常用于物流、调度等问题，可以找到满足各种限制条件的最佳配置。 6. **线性规划求解器**：如Gurobi、CPLEX等，它们能够高效地解决大规模的线性和混合整数规划问题，是现代商业优化中的关键组件。 数学规划模型在实际应用中，通常会涉及以下步骤： 1. **问题定义**：明确优化的目标和约束条件，例如最大化利润、最小化成本等。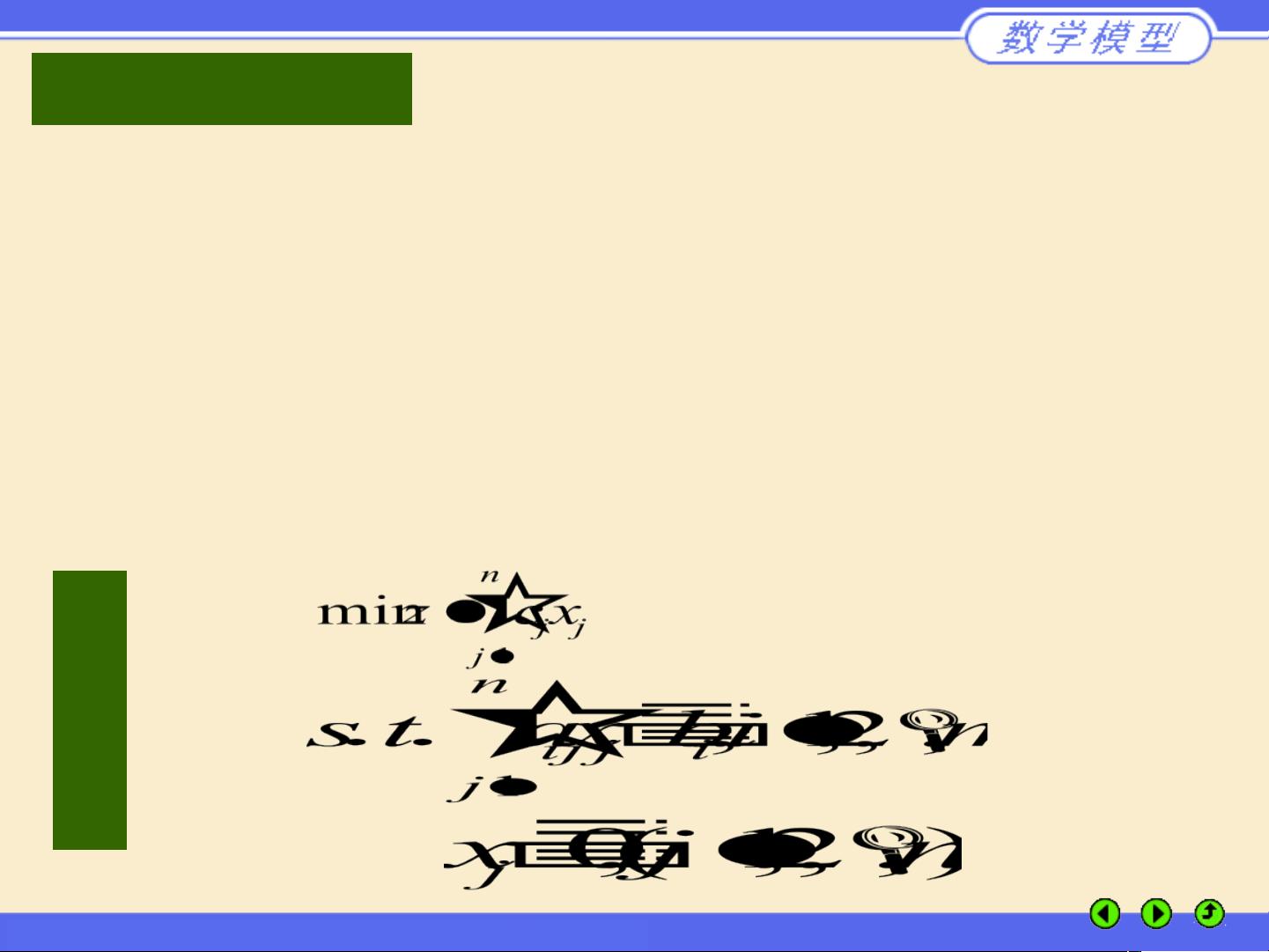 2. **建模**：将问题转化为数学表达式，包括目标函数和约束条件。 3. **求解**：使用适当的算法或求解器寻找最优解。 4. **结果分析**：解释和理解模型的解，评估其对实际问题的适用性。 5. **实施与调整**：根据模型结果进行决策，并可能根据反馈调整模型。 在“资料整理”中，可能包含了关于如何构建数学规划模型的实例、案例分析以及解题技巧等内容，这对于理解和掌握这一技术至关重要。学习并熟练运用数学规划模型，不仅可以提升问题解决能力，也能为数据分析和决策制定提供强有力的支持。