#### 知识点归纳
- 同步和异步:
在离散时间更新状态 => 同步时序系统
在任意时间更新状态 =>异步时序系统
$$
eg:对D触发器来讲,异步加在SR端,同步加在D端
$$
- 数制转换的小数部分:数值的小数部分重复乘以新的基数,保存结果的整数部分,直到小数部分为0。新的数制下的数字按计算结果的整数顺序排列。如果新的基数 > 10, 把所有大于10的余数用数字A, B, … 表示
$$
eg:0.6875转换为2进制,\\
0.6875\times2=1.375,\\0.375\times2=0.75,\\0.75\times2=1.5,\\0.5\times2=1;\\
0.6875=2^{-1}+2^{-3}+2^{-4}=0.1011
$$
注意添0
- 标准形式:
积之和(SOP):找1项
和之和(POS):找0项
- 成本标准:
文字成本 (L):数字母数
$$
eg:F = BD + AB'C + A C'D'\\ L = 8
$$
门输入成本(G):L+与或门数(两个以上字母在一起的个数)
$$
eg:F = BD + AB’C + AC’D’\\ G = 11
$$
含非门的门输入成本(GN):L+G+非门数(一种字母计算一次)
$$
eg:F = BD+AB’C+AB’D’+ABC’ \\GN=18
$$
- 缓冲器:是一个电子信号放大器,以便于输出端可以连接更多的门,或者用来减少信号通过电路的时间
F=X:
- 与非门(与完再非),等价于非完再或
或非门(或完再非),等价于非完再与
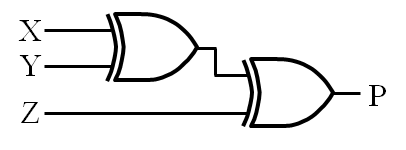
- 异或运算的拓展(用于全加器)
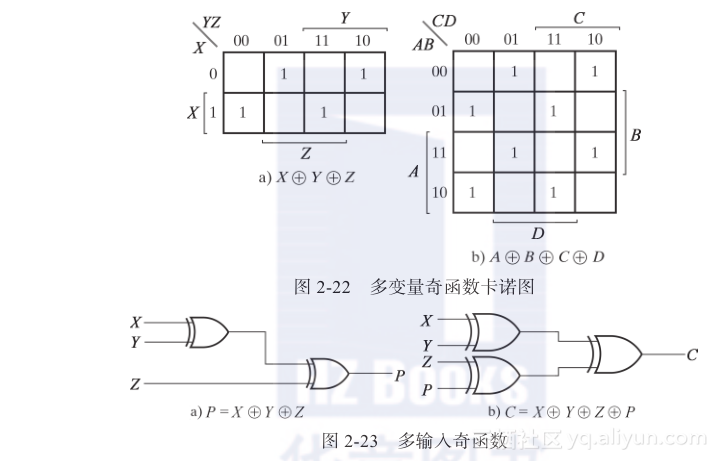
奇函数:与二变量函数**只需要一个变量的值为1**相比,三变量或者三变量以上的函数则**需要奇数个变量的值为1**。所以,**多变量异或运算**又被定义为奇函数(odd function)。事实上,严格说来,这才是三变量或者三变量以上运算的正确含义,“异或”这个名字只适合于二变量。
奇函数的反/倒相即偶函数
奇函数和偶函数在卡诺图上呈现“跳棋棋盘” 样式(如图)
奇函数的卡诺图中标有1的格子对应于最小项,它的索引号(二进制)含奇数个1,偶函数则含偶数个1.
$$
eg:下图为1项为:001,010,100,111,均含奇数个1
$$
- 校验/产生偶校验字:用奇函数
校验/产生奇校验字:用偶函数
eg:
n = 3. 产生一个4位偶校验字的校验位,使用奇函数:
操作: (X,Y,Z) = (0,0,1) ,P=1
(X,Y,Z,P) = (0,0,1,1) , E = 0.
如果传输时Y从0变成1,那么E = 1表示错误.
- 三态门与高阻态输出:
三个输出状态:0,1,Hi-Z
加了Hi-Z后逻辑门的特性:
- 有三个输出值
- **能把两个输出端连在一起(期中考点)**
- 信号能从两个方向向另一个方向进行单向传输
- 三态缓冲器:
数据输入IN加控制输入(使能)EN
EN:OUT=Hi-Z
~EN:OUT=IN
eg:把两个三态缓冲器的输出B1和B0连在一起, 成为一个输出端OUT
假设:缓冲器的输入可以是任意0和 1的组合
规则:至少一个缓冲器的输出值必须为Hi-Z,为什么?
因为输入可以是任意的组合,包括(0,1)和(1,0),若没有Hi-Z输出,则可能会产生高电流,破坏电路。
对两个三态门的连接,有多少个有效的输入输出组合存在?
5
对n个三态缓冲器输出端连接成一个输出,有什么规则?
n-1个输出必须为Hi-Z
有多少个有效的输入输出组合存在?
2n+1:每个缓冲器可输出0、1,则其他全为Hi-Z,2n种组合,加上全为Hi-Z,即2n+1.
三态逻辑用于数据选择:
优点:由于 EN0 = ~S 以及EN1 = S, 其中一个三态缓冲器的输出总是Hi-Z,OL总是分别由IN0和IN1确定

- 基本逻辑函数:
定值:F=0,F=1
传递:F=X
取反:F=~X
- 译码器的扩展:对原始的两个译码器的输出端分别用与门相连
eg:两个1-2译码器构成2-4译码器

- 译码器加或门实现通用逻辑(原理:最小项之和)
eg:
P1、P2、P4分别为A7、A6、A5、A3的函数,先将4位A进行4-16译码,有16个输出,对应16个最小项,再对3位P求最小项之和,用或门实现求和
P1 = Sum(1,2,5,6,8,11,12,15)
P2 = Sum(1,3,4,6,8,10,13,15)
P4 = Sum(2,3,4,5,8,9,14,15)

- 优先编码器:
因为译码器的输出只有一个为1,对其简单的反操作不能适应所有的输入组合,比如出现两个1。
一个适合于任意输入组合,并能产生有意义的结果的编码器称为优先编码器。在所有出现的1中,选择输入值位置包含1的最高位(或者最低位),来产生这个位置对应的二进制编码。
eg:
只考虑1项,如A1的1项为8、4,分别为D4'D3和D4'D3'D2,再求和


- 多路复用器:
- 译码器+使能+或门
eg:4-1多路复用器,选择端S1S0经2-4译码后,产生4项。只有1项为1,与门和输入连接,故只有一个输入有效,再或门输出这一个有效值。

- 三态门:每个选择端选择一半,持续二分选出最后一个
eg:

- 多路复用器实现通用组合电路:
- 直接接定值(0、1)信号
对A->B的问题,先按A从大到小进行排序,再分别对B的每一位进行定值选择
eg:


以y为例,重新排序后,从000-111,y的对应输出为0、1、1、0、0、1、1、0。以000为例,内部即以IN1输入输出,故IN1接定值0即可,以此类推:
》读书笔记,结合期末复习提纲,为复旦大学大二上专业课《数字逻辑与部件设计》所写.zip
需积分: 0 53 浏览量
更新于2024-03-22
收藏 10KB ZIP 举报
《逻辑与计算机设计基础》是计算机科学领域的一本经典教材,尤其对于学习数字逻辑与部件设计的大学生来说,它是深入理解计算机硬件基础的重要资源。第五版的书籍通常会包含最新的理论和技术更新,使得内容更加贴近现代计算机系统的发展。这篇读书笔记结合了期末复习提纲,旨在帮助复旦大学大二学生更好地理解和掌握课程内容,为他们的期末考试和毕业设计提供有力支持。
笔记首先可能涵盖了逻辑门电路的基本概念,包括AND、OR、NOT、NAND、NOR和XOR等逻辑运算符,以及它们的真值表和布尔表达式。这些基本逻辑元素是构建更复杂电路的基础,也是理解计算机硬件工作原理的入门知识。
笔记可能详细讲解了组合逻辑电路的设计,如半加器、全加器、编码器、译码器、数据选择器和多路复用器等。这些电路在处理数据时起着至关重要的作用,例如在算术逻辑单元(ALU)中,全加器用于执行基本的算术运算。
在时序逻辑方面,笔记可能涵盖了寄存器、计数器、移位寄存器等,这些都是构建存储和处理信息的动态结构的关键。特别是同步和异步计数器的区别,以及它们在计算机时钟和数据处理中的应用。
此外,笔记还可能深入到摩尔(Moore)和米利(Mealy)型状态机的设计,以及如何使用状态图和状态表来描述和实现有限状态自动机。这些知识在设计微控制器和嵌入式系统的控制逻辑中非常关键。
对于计算机部件设计,笔记可能会讨论CPU的组成,包括指令集架构、运算器、控制器、内存接口等。特别是流水线技术,这是提高处理器性能的重要手段,通过并行处理不同阶段的指令,可以显著提升处理速度。
至于源码部分,可能是作者为了辅助理解书中理论,编写的一些简单示例代码或实验程序。这些代码可能使用某种编程语言(如C、Python或Verilog)实现逻辑门、组合逻辑电路或简单的时序逻辑设计,帮助学生将理论知识转化为实践操作。
期末考试复习提纲通常会突出课程的重点和难点,比如数字系统的设计方法、故障检测与校正、高速数字设计的挑战等。学生们应该根据自己的理解和掌握情况,对提纲中的每个知识点进行深入学习和练习。
对于毕设来说,学生需要综合运用所学知识,可能涉及到设计一个小型的数字系统,比如简单的计算器或数字信号处理器。源码和笔记可以帮助他们规划项目,解决遇到的问题,并为最终的项目演示做好准备。
这份资料集合为复旦大学的学生提供了一个全面的学习资源,既包含了理论知识的梳理,也有实际操作的指导,有助于他们在数字逻辑与部件设计的学习道路上取得优异成绩。
探索电平
- 粉丝: 674
- 资源: 1716
最新资源
- 人物检测26-YOLO(v5至v11)、COCO、CreateML、Paligemma、TFRecord、VOC数据集合集.rar
- 人和箱子检测2-YOLO(v5至v11)、COCO、CreateML、Paligemma、TFRecord、VOC数据集合集.rar
- 清华大学2022年秋季学期 高等数值分析课程报告
- GEE错误集-Cannot add an object of type <Element> to the map. Might be fixable with an explicit .pdf
- 清华大学2022年秋季学期 高等数值分析课程报告
- 矩阵与线程的对应关系图
- 人体人员检测46-YOLO(v5至v9)、COCO、Darknet、TFRecord数据集合集.rar
- GEMM优化代码实现1
- java实现的堆排序 含代码说明和示例.docx
- 资料阅读器(先下载解压) 5.0.zip














