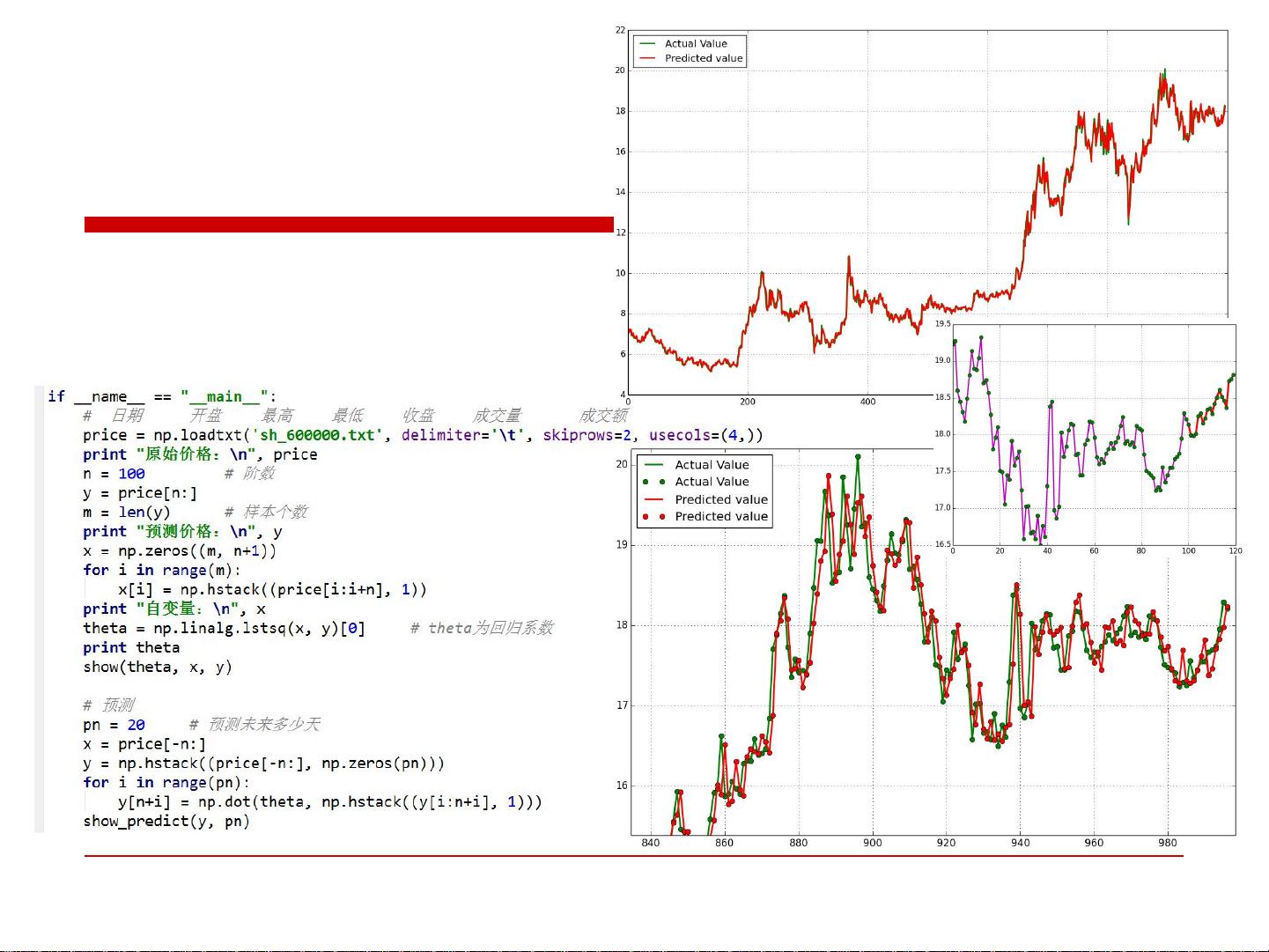
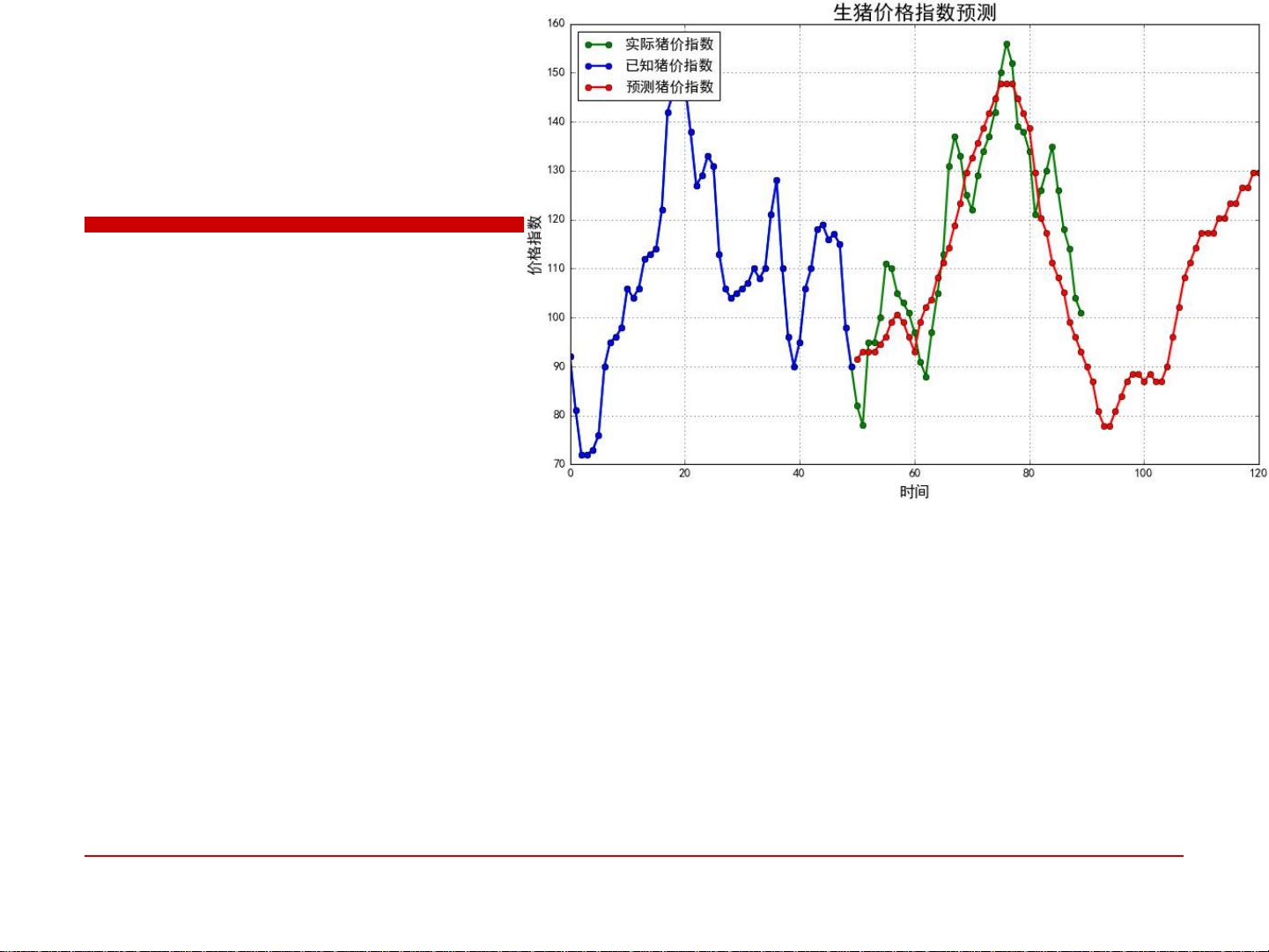
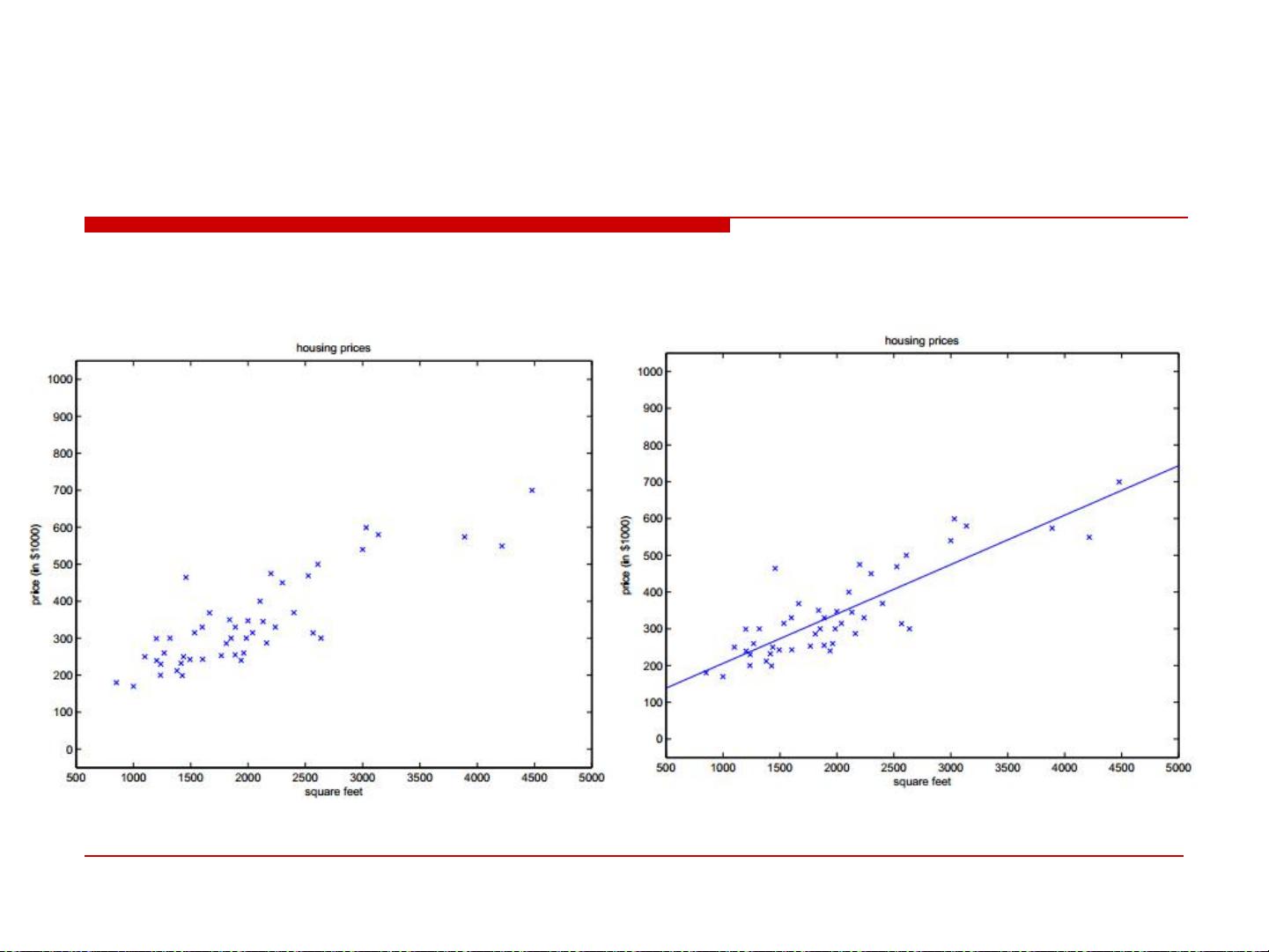
【内容大纲】 1.Python与数学基础 共83页.pdf 1.矩阵和线性代数_Python 共90页.pdf 2.概率论与数理统计 共89页.pdf 3.数据清洗和特征选择 共16页.pdf 4.多元回归与逻辑回归 共69页.pdf 5.决策树随机森林 共91页.pptx 6.支持向量机 共70页.pdf 7.聚类 共88页.pdf 8.EM算法 共66页.pptx 9.HMM 共80页.pptx 10.主题模型 共78页.pdf 11.卷积神经网络 共76页.pdf 12.目标检测算法 共47页.pdf 12卷积神经网络 共76页.pdf 13.RNN 共47页.pptx 14.NLP技术分享 自然语言处理技术课程 共184页.pdf 15.GAN网络 共25页.pdf 15.GAN源代码讲解及GAN项目介绍 共24页.pdf 16.强化学习-课件 共125页.pdf ### Python人工智能课程知识点详解 #### 一、多元回归与逻辑回归概述 本章节主要介绍了多元回归与逻辑回归的基础概念及其在Python机器学习与深度学习中的应用。这些算法是数据分析和预测建模的重要组成部分。 ##### 1. 多元回归 - **定义**: 多元回归是一种用于预测一个连续变量(因变量)基于一个或多个自变量的方法。 - **应用场景**: 股价预测、生猪价格预测等。 - **模型公式**: \[ y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + ... + \theta_n x_n \] 其中 \( y \) 是预测的目标变量,\( \theta_i \) 表示权重系数,\( x_i \) 是自变量。 ##### 2. 逻辑回归 - **定义**: 逻辑回归主要用于解决二分类问题,也可以扩展到多分类问题(例如Softmax回归)。 - **应用场景**: 分类问题的首选算法。 - **模型公式**: \[ P(y=1|x;\theta) = h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}} \] 其中 \( P(y=1|x;\theta) \) 表示给定输入 \( x \) 和参数 \( \theta \) 的情况下,输出 \( y \) 为 1 的概率。 #### 二、多元回归详解 - **线性回归**: 最简单的形式是单变量线性回归,即只有一个自变量的情况。当存在多个自变量时,称为多元线性回归。 - **多元线性回归模型**: \[ h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + ... + \theta_n x_n \] - **最小二乘法**: 一种常用的方法来估计模型参数 \( \theta \),通过最小化预测值与实际值之间的平方误差之和来实现。 \[ J(\theta) = \frac{1}{2m} \sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 \] 其中 \( m \) 是样本数量,\( h_\theta(x^{(i)}) \) 是预测值,\( y^{(i)} \) 是实际值。 - **极大似然估计(MLE)**: MLE 是另一种估计参数的方法,它假设误差项是独立同分布的,并且服从均值为 0、方差为 \( \sigma^2 \) 的高斯分布。 \[ L(\theta; X, y) = \prod_{i=1}^{m} p(y^{(i)}|x^{(i)}; \theta) \] 其中 \( p(y^{(i)}|x^{(i)}; \theta) \) 是给定 \( x^{(i)} \) 和参数 \( \theta \) 下的条件概率。 #### 三、逻辑回归详解 - **Sigmoid 函数**: 逻辑回归的核心函数,用于将线性回归的结果映射到 [0, 1] 区间内,表示属于某个类别的概率。 \[ g(z) = \frac{1}{1+e^{-z}} \] - **目标函数**: 逻辑回归的目标函数通常是最大化对数似然函数。 \[ l(\theta) = \sum_{i=1}^{m} [y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)}))] \] - **梯度下降算法**: 一种迭代优化算法,用于最小化成本函数,从而找到最佳的模型参数 \( \theta \)。 \[ \theta_j := \theta_j - \alpha \sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \] 其中 \( \alpha \) 是学习率,\( j \) 表示第 \( j \) 个特征。 #### 四、案例分析 - **股价预测**: 使用自回归方法,考虑过去的价格作为输入,预测未来的股价。 - **生猪价格预测**: - **背景**: 生猪期货市场中,价格波动较大,大型和中型养殖户为主要参与者。 - **直接意义**: 预测未来半年到一年的生猪价格,对决定当前养殖规模具有重要意义。 - **模型实践**: 使用历史生猪价格建立模型,通过回测数据验证模型的有效性。 #### 五、模型评估与优化 - **特征选择**: 选择对模型预测能力贡献最大的特征,减少冗余信息。 - **假设的重要性**: - **内涵性**: 假设通常基于常识,大多数情况下是正确的,但可能不总是适用。 - **简化性**: 为了简化计算和模型理解,需要做一些近似。 - **发散性**: 即使假设不完全正确,得出的结论也可能在实践中有效。 #### 六、参数求解 - **参数的解析解**: \[ \theta = (X^TX)^{-1}X^Ty \] 当 \( X^TX \) 不可逆或为了防止过拟合,可以通过添加正则化项(例如 \( \lambda I \))来解决。 \[ \theta = (X^TX + \lambda I)^{-1}X^Ty \] ### 总结 多元回归与逻辑回归是机器学习中非常重要的模型,它们不仅适用于连续和离散的数据预测,而且通过合适的参数调整和技术选择,可以在多种应用场景中发挥重要作用。理解这些模型的基本原理、应用场景以及优化技巧对于从事数据分析和机器学习的人员来说至关重要。


剩余68页未读,继续阅读

- 粉丝: 467
- 资源: 7835




 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功