数学建模培训教程 数学模型第四版课后答案 作业答案 共55页.pdf
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
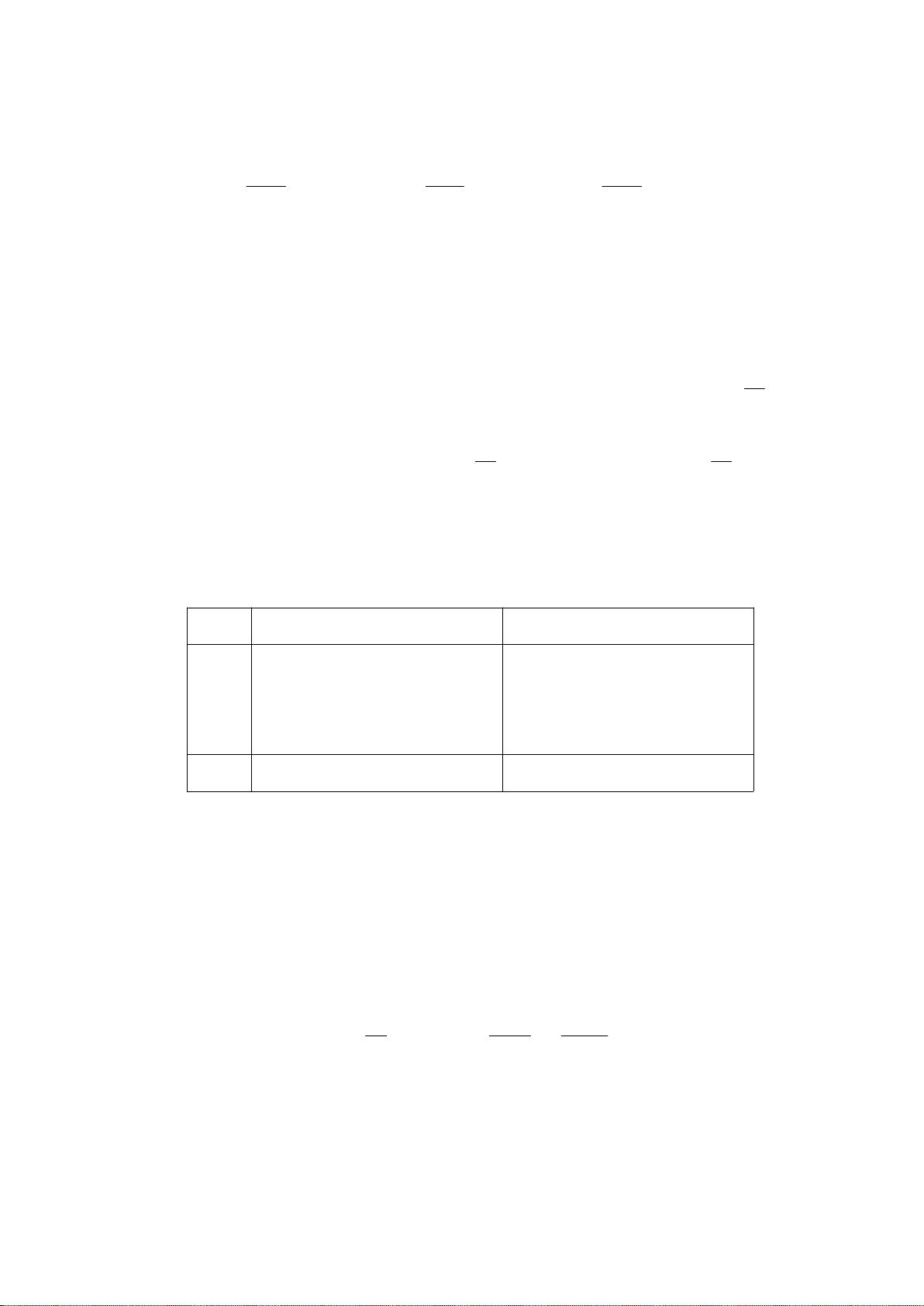
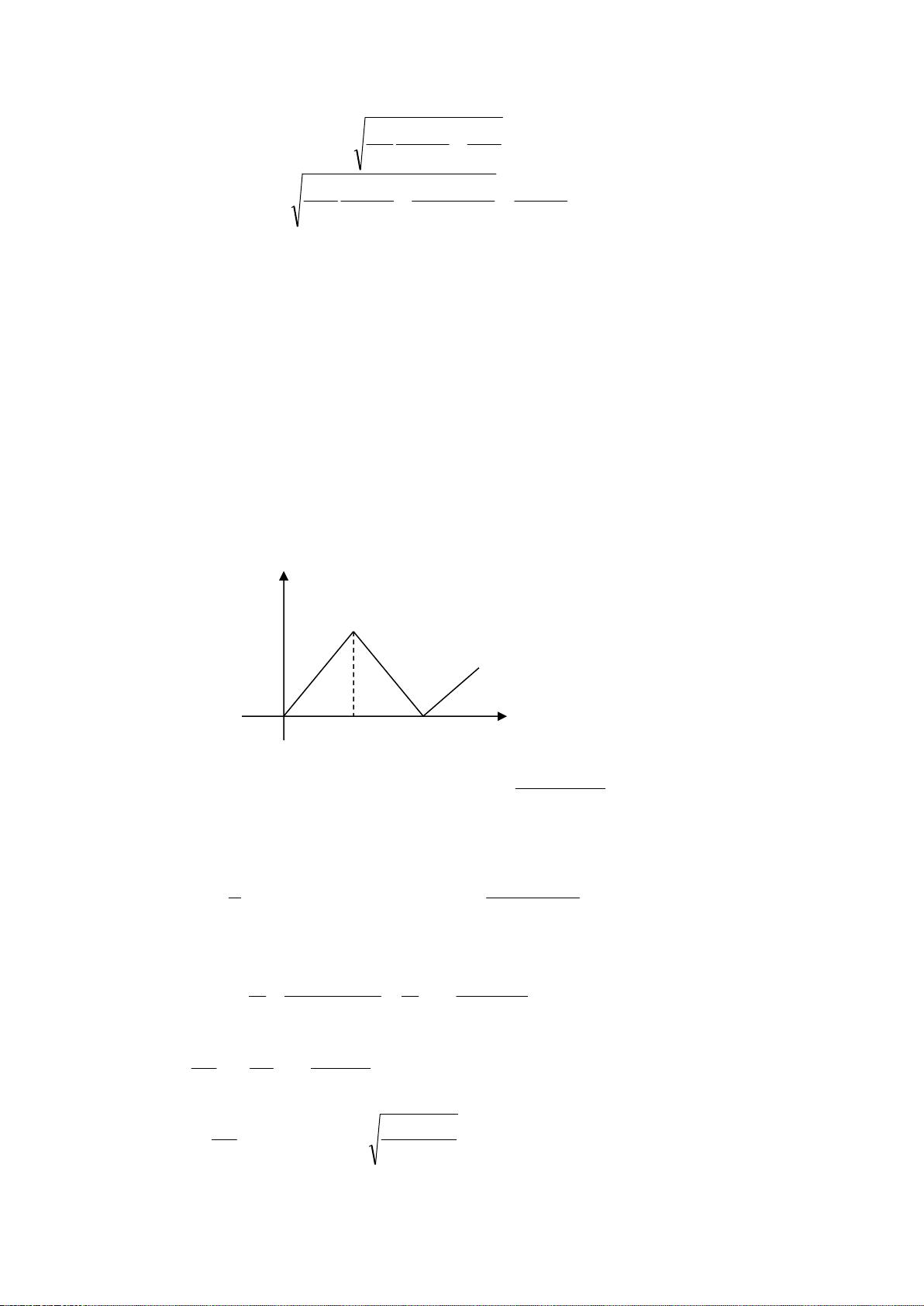
《数学模型》作业答案 第二章(1)(2012 年12 月21 日) 1. 学校共1000 名学生,235 人住在A 宿舍,333 人住在B 宿舍,432 人住在C 宿舍.学生们 要组织一个10 人的委员会,试用下列办法分配各宿舍的委员数: (1). 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者; (2). §1 中的Q 值方法; (3).d’Hondt 方法:将A、B、C 各宿舍的人数用正整数n=1,2,3,……相除,其商数 如下表: 《数学模型》是一本关于应用数学解决实际问题的教材,其中包含了各种数学建模的方法和技术。在提供的作业答案中,我们可以看到三个不同的方法用于分配一个10人委员会的席位,这些方法涉及到公平和比例原则。 1. **按比例分配取整数的名额**:这是一种基于各组人数比例的分配方式。计算各宿舍的学生比例,然后取整分配席位,剩余的席位根据小数部分大小进行分配。例如,A、B、C宿舍分别有235、333、432人,按比例分配后,初步得到3个席位给A,3个给B,4个给C。剩下的席位,因为B的小数部分最大,所以它会获得剩余的一个席位。 2. **Q值方法**:这种方法是通过计算Q值来决定额外席位的归属。Q值是每个宿舍剩余席位数与其人数的比例,选择Q值最大的宿舍获得额外席位。当委员会规模扩大到15人时,Q值方法依然适用,会使得席位更均衡地分配给各个宿舍。 3. **d’Hondt方法**:这是一种基于除法的分配方式,将宿舍人数除以连续的自然数,取最大商数作为分配依据。例如,将A、B、C宿舍的人数分别除以1、2、3等,然后选取最大的10个商,对应的宿舍获得席位。这种方法旨在使得每个席位代表的人数尽量接近。 在10人委员会的情况下,三种方法都给出了类似的分配结果,但在15人委员会时,由于席位的增加,分配结果会有变化。d’Hondt方法和Q值方法通常能提供更公平的分配,尤其是当群体规模变化时。 此外,作业还涉及了微积分在建立数学模型中的应用。例如,录像带记数器读数与转过时间的关系可以通过微积分来描述。设录像带记数器读数为n,转过的时间为t,通过积分可以得到两者之间的关系式,从而构建数学模型。 这些数学模型和方法在解决实际问题时起着关键作用,如决策制定、资源分配和系统优化。它们不仅需要对数学理论的深入理解,还需要灵活应用这些理论来解决现实世界的复杂问题。通过这样的数学建模训练,学生能够提升分析问题和解决问题的能力,更好地理解和应用数学知识。

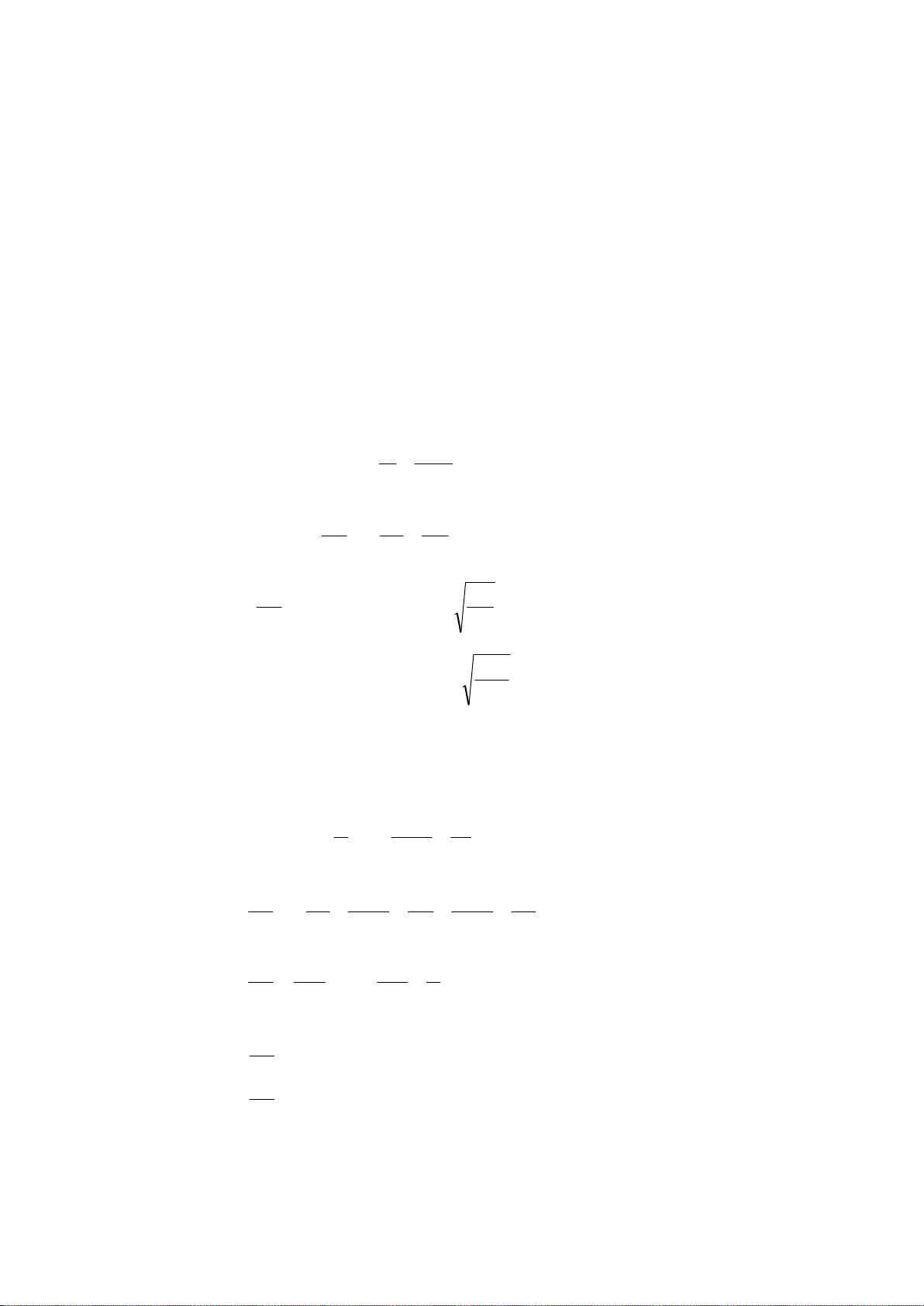

剩余57页未读,继续阅读

- 粉丝: 457
- 资源: 7362




 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜 信息提交成功
信息提交成功

