数据结构和算法必知必会的50个代码实现.zip

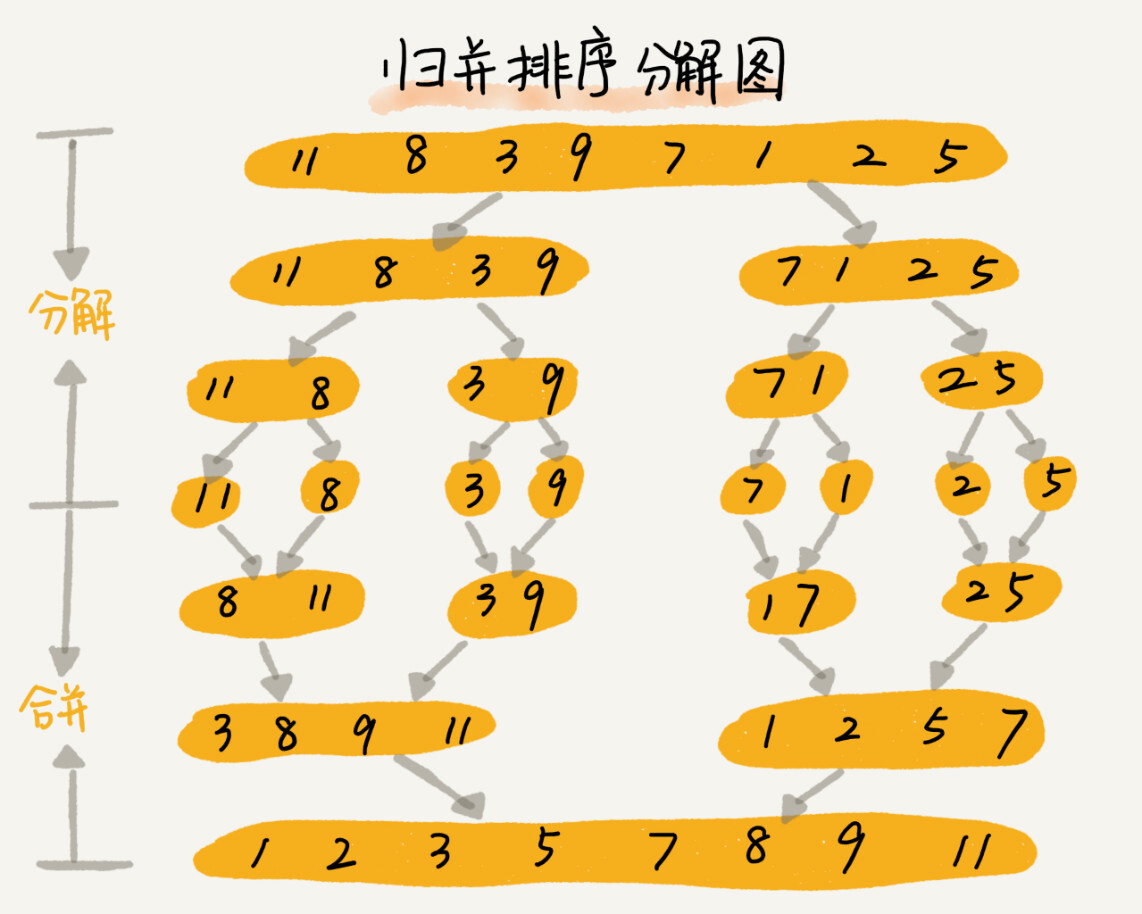
# 排序（线性对数时间复杂度排序算法） 开篇问题：如何在 $O(n)$ 时间复杂度内寻找一个无序数组中第 K 大的元素？ ## 归并排序 * 归并排序使用了「分治」思想（Divide and Conquer） * 分：把数组分成前后两部分，分别排序 * 合：将有序的两部分合并  * 分治与递归 * 分治：解决问题的处理办法 * 递归：实现算法的手段 * ——分治算法经常用递归来实现 * 递归实现： * 终止条件：区间 `[first, last)` 内不足 2 个元素 * 递归公式：`merge_sort(first, last) = merge(merge_sort(first, mid), merge_sort(mid, last))`，其中 `mid = first + (last - first) / 2` C++ 实现： ```cpp template <typename FrwdIt, typename T = typename std::iterator_traits<FrwdIt>::value_type, typename BinaryPred = std::less<T>> void merge_sort(FrwdIt first, FrwdIt last, BinaryPred comp = BinaryPred()) { const auto len = std::distance(first, last); if (len <= 1) { return; } auto cut = first + len / 2; merge_sort(first, cut, comp); merge_sort(cut, last, comp); std::vector<T> tmp; tmp.reserve(len); detail::merge(first, cut, cut, last, std::back_inserter(tmp), comp); std::copy(tmp.begin(), tmp.end(), first); } ``` 这里涉及到一个 `merge` 的过程，它的实现大致是： ```cpp namespace detail { template <typename InputIt1, typename InputIt2, typename OutputIt, typename BinaryPred = std::less<typename std::iterator_traits<InputIt1>::value_type>> OutputIt merge(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt d_first, BinaryPred comp = BinaryPred()) { for (; first1 != last1; ++d_first) { if (first2 == last2) { return std::copy(first1, last1, d_first); } if (comp(*first2, *first1)) { *d_first = *first2; ++first2; } else { *d_first = *first1; ++first1; } } return std::copy(first2, last2, d_first); } } // namespace detail ```  ### 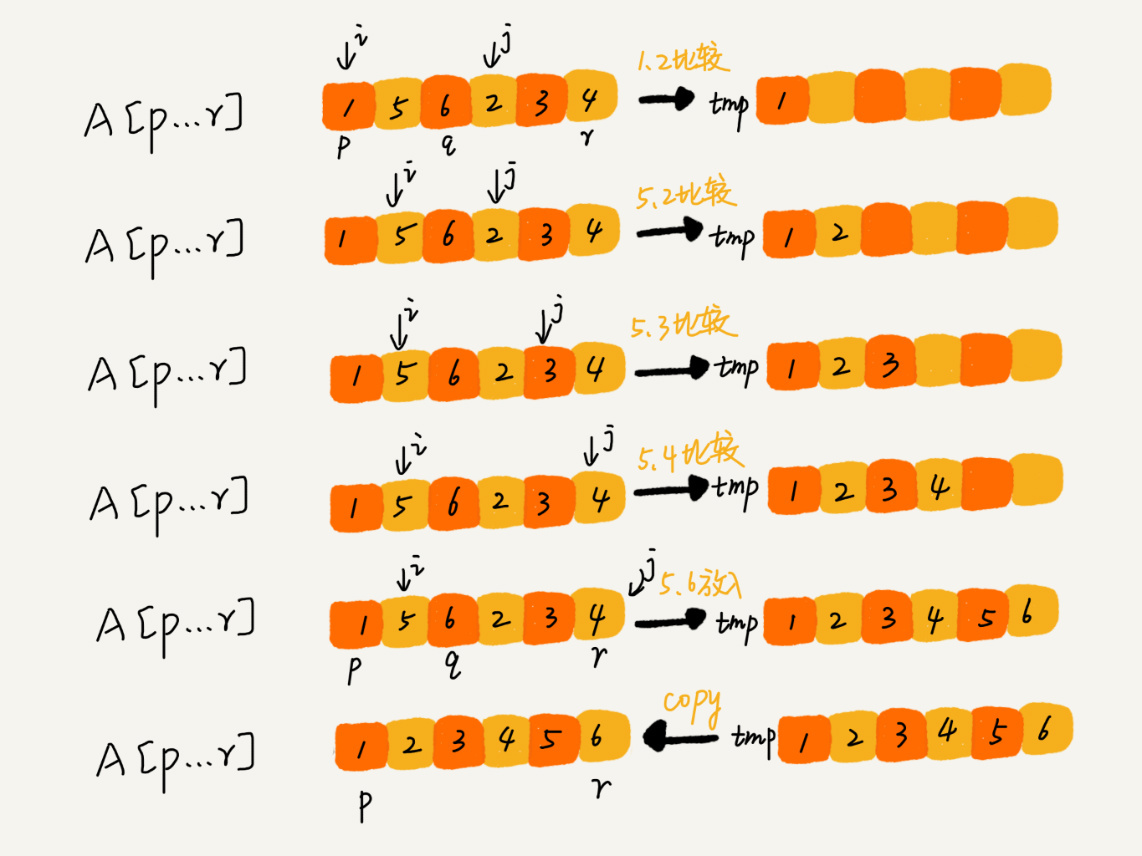算法分析 * 稳定性 * 由于 `comp` 是严格偏序，所以 `!comp(*first2, *first1)` 时，取用 `first1` 的元素放入 `d_first` 保证了算法稳定性 * 时间复杂度 * 定义 $T(n)$ 表示问题规模为 $n$ 时算法的耗时， * 有递推公式：$T(n) = 2T(n/2) + n$ * 展开得 $T(n) = 2^{k}T(1) + k * n$ * 考虑 $k$ 是递归深度，它的值是 $\log_2 n$，因此 $T(n) = n + n\log_2 n$ * 因此，归并排序的时间复杂度为 $\Theta(n\log n)$ * 空间复杂度 * 一般来说，空间复杂度是 $\Theta(n)$ ## 快速排序（quick sort，快排） 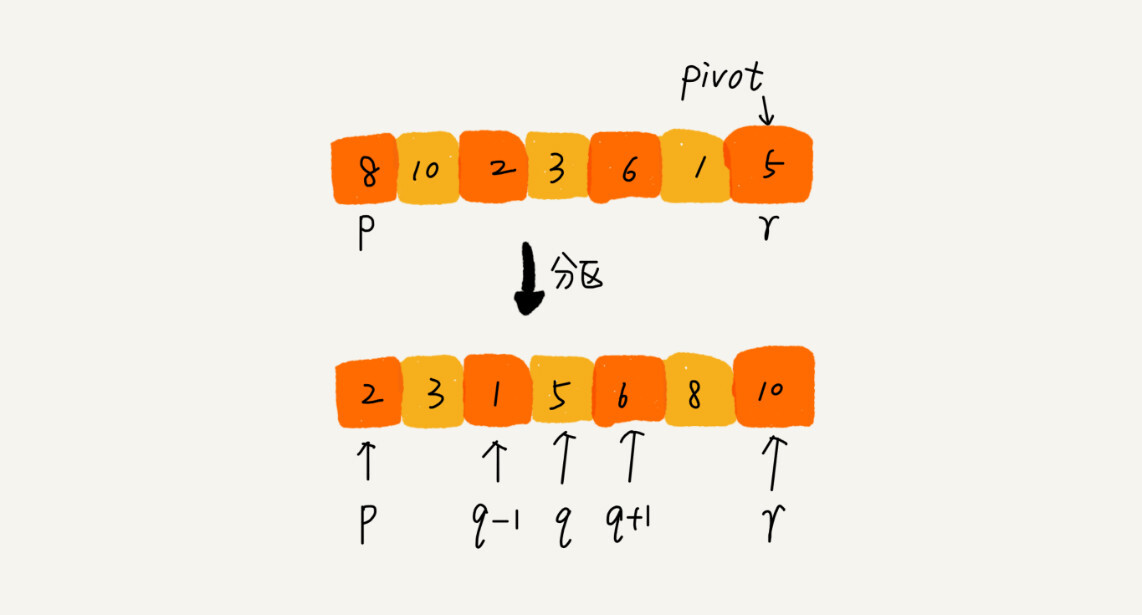原理： * 在待排序区间 `[first, last)` 中选取一个元素，称为主元（pivot，枢轴） * 对待排序区间进行划分，使得 `[first, cut)` 中的元素满足 `comp(element, pivot)` 而 `[cut, last)` 中的元素不满足 `comp(element, pivot)` * 对划分的两个区间，继续划分，直到区间 `[first, last)` 内不足 2 个元素  显然，这又是一个递归： * 终止条件：区间 `[first, last)` 内不足 2 个元素 * 递归公式：`quick_sort(first, last) = quick_sort(first, cut) + quick_sort(cut, last)` ```cpp template <typename IterT, typename T = typename std::iterator_traits<IterT>::value_type> void quick_sort(IterT first, IterT last) { if (std::distance(first, last) > 1) { IterT prev_last = std::prev(last); IterT cut = std::partition(first, prev_last, [prev_last](T v) { return v < *prev_last; }); std::iter_swap(cut, prev_last); quick_sort(first, cut); quick_sort(cut, last); } } ``` > 一点优化（Liam Huang）：通过将 `if` 改为 `while` 同时修改 `last` 迭代器的值，可以节省一半递归调用的开销。 ```cpp template <typename IterT, typename T = typename std::iterator_traits<IterT>::value_type> void quick_sort(IterT first, IterT last) { while (std::distance(first, last) > 1) { IterT prev_last = std::prev(last); IterT cut = std::partition(first, prev_last, [prev_last](T v) { return v < *prev_last; }); std::iter_swap(cut, prev_last); quick_sort(cut, last); last = cut; } } ``` 如果不要求空间复杂度，分区函数实现起来很容易。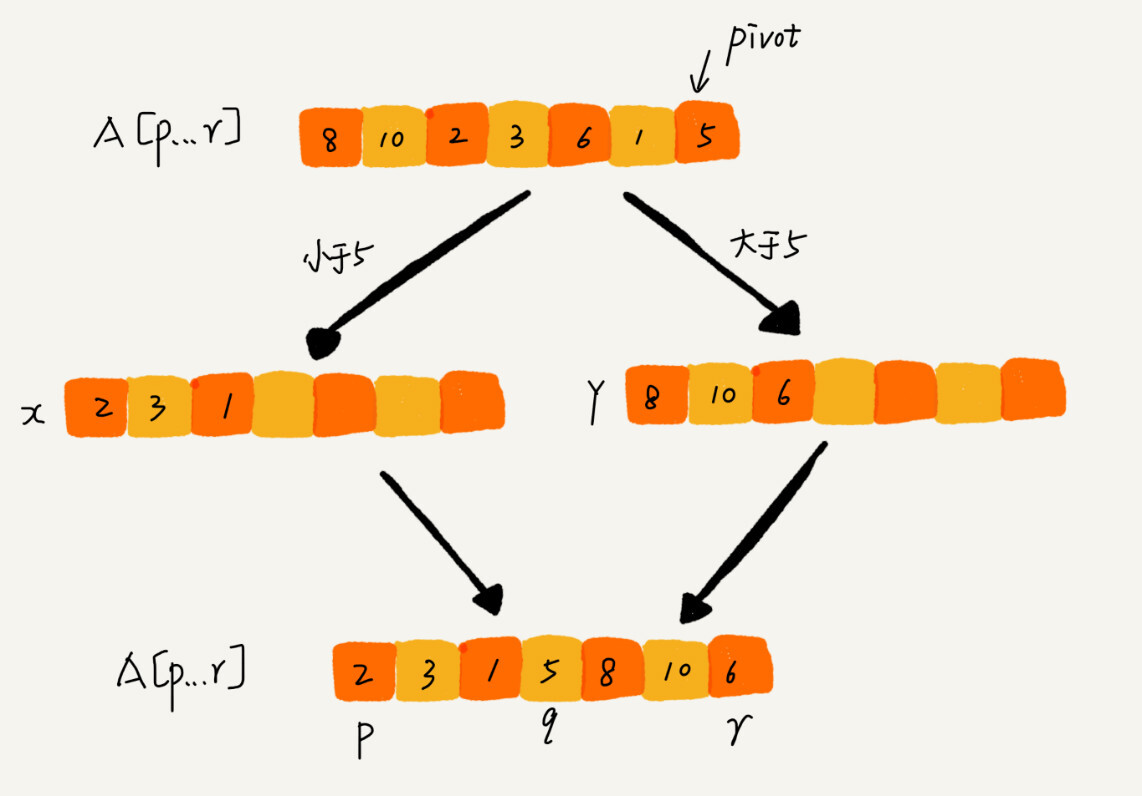  若要求原地分区，则不那么容易了。下面的实现实现了原地分区函数，并且能将所有相等的主元排在一起。 ```cpp template <typename BidirIt, typename T = typename std::iterator_traits<BidirIt>::value_type, typename Compare = std::less<T>> std::pair<BidirIt, BidirIt> inplace_partition(BidirIt first, BidirIt last, const T& pivot, Compare comp = Compare()) { BidirIt last_less, last_greater, first_equal, last_equal; for (last_less = first, last_greater = first, first_equal = last; last_greater != first_equal; ) { if (comp(*last_greater, pivot)) { std::iter_swap(last_greater++, last_less++); } else if (comp(pivot, *last_greater)) { ++last_greater; } else { // pivot == *last_greater std::iter_swap(last_greater, --first_equal); } } const auto cnt = std::distance(first_equal, last); std::swap_ranges(first_equal, last, last_less); first_equal = last_less; last_equal = first_equal + cnt; return {first_equal, last_equal}; } ``` ### 算法分析 * 稳定性 * 由于 `inplace_partition` 使用了大量 `std::iter_swap` 操作，所以不是稳定排序 * 时间复杂度 * 定义 $T(n)$ 表示问题规模为 $n$ 时算法的耗时， * 有递推公式：$T(n) = 2T(n/2) + n$（假定每次分割都是均衡分割） * 展开得 $T(n) = 2^{k}T(1) + k * n$ * 考虑 $k$ 是递归深度，它的值是 $\log_2 n$，因此 $T(n) = n + n\log_2 n$ * 因此，快速排序的时间复杂度为 $\Theta(n\log n)$ * 空间复杂度 * 一般来说，空间复杂度是 $\Theta(1)$，因此是原地排序算法 ## 开篇问题 * 分区，看前半段元素数量 * 前半段元素数量 < K，对后半段进行分区 * 前半段元素数量 > K，对前半段进行分区 * 前半段元素数量 = K，前半段末位元素即是所求