Adiscreteparticleswarmoptimization资源-CSDN文库

DPSO

需积分: 9 61 浏览量 2014-09-29 20:30:07 上传评论收藏 234KB PDF 举报

资源推荐

资源详情

资源评论

Discrete Optimization

A discrete particle swarm optimization for lot-strea ming

ﬂowshop scheduling problem

Chao-Tang Tseng

, Ching-Jong Liao

Department of Industrial Engineering and Management, Chaoyang University of Technology, Taichung County 413, Taiwan

Department of Industrial Management, National Taiwan University of Science and Technology, 43 Keelung Road,

Section 4, Taipei 106, Taiwan

Received 26 March 2006; accepted 24 August 2007

Available online 7 September 2007

Abstract

We consider an n-job, m-machine lot-streaming problem in a ﬂowshop with equal-size sublots where the objective is to

minimize the total weighted earliness and tardiness. To solve this problem, we ﬁrst propose a so-called net beneﬁt of move-

ment (NBM) algorithm, which is much more eﬃcient than the existing linear programming model for obtaining the opti-

mal starting and completion times of sublots for a given job sequence. A new discrete particle swarm optimization (DPSO)

algorithm incorporating the NBM algorithm is then developed to search for the best sequence. The new DPSO improves

the existing DPSO by introducing an inheritance scheme, inspired by a genetic algorithm, into particles construction. To

verify the proposed DPSO algorithm, comparisons with the existing DPSO algorithm and a hybrid genetic algorithm

(HGA) are made. Computational results show that the proposed DPSO algorithm with a two-point inheritance scheme

is very competitive for the lot-streaming ﬂowshop scheduling problem.

Keywords: Lot streaming; Particle swarm optimization; Metaheuristic; Scheduling; Weighted earliness and tardiness

1. Introduction

In a traditional ﬂowshop, each job must be pro-

cessed on every machine and all jobs must follow

the same machine sequence (rout e). One of the com-

mon restrictions made in most research studies is

that a job cannot be transferred to the next machine

before its processing is ﬁnished. This need not be the

case in many practical situations because a job may

be split into a number of smaller sublots. When a

job sublot is completed, it can be immediately

moved to the next machine. By splitting jobs, the

idle time on successive machines can be reduced.

The job splitting into sublots process is usually

called ‘‘lot streaming’’, which was ﬁrst introduced

by Reiter (1966). Some studies showed that lot

streaming can signiﬁcantly improve the schedule

performance with respect to the makespan (Potts

and Baker, 1989; Baker and Pyke, 1990). In recent

years, lot streaming has received extensive attention

and bee n applied to the ﬂowshop scheduling prob-

lem. A complete survey can be found in Chang

and Chiu (2005).

doi:10.1016/j.ejor.2007.08.030

Corresponding author. Fax: +886 2 27376344.

E-mail address: cjl@im.ntust.edu.tw (C.-J. Liao).

Available online at www.sciencedirect.com

European Journal of Operational Research 191 (2008) 360–373

www.elsevier.com/locate/ejor

For the lot-streaming problem of a single job in a

ﬂowshop, the objective is to simply determine the

optimal sublot sizes. Potts and Baker (1989) consid-

ered a ﬂowshop with makespan criterion and indi-

cated when it is suﬃcient in a single-job model to

use the same sublot sizes for all machines. Trietsch

and Baker (1993) reviewed the diﬀerent forms of

single-job lot streaming existing in the literature

and generalized some important struc tural insights.

To minimize the total ﬂow time, Kropp and Smunt

(1990) presented optimal sublot size policies and

two heuristic methods for a single job in a ﬂowshop.

Bukchin et al. (2002) identi ﬁed the optimal solution

properties and developed a solution procedure to

minimize the total ﬂow time in a two-machine ﬂow-

shop with detached setups and batch availability.

For the lot-streaming problem with n jobs

(j =1,... ,n) in a ﬂowshop with makespan criterion,

we need to simultaneously obtain the best job

sequence and the optimal sublot allocation (sublot

starting and completion times). Potts and Baker

(1989) showed that it is not possible to solve the

n-job problem sim ply by applying lot streaming

individually to the single-job problem. Vickson

and Alfredsson (1992) modiﬁed Johnson’s rule to

obtain the optimal solutions for the two-machine

and special three-machine prob lems with unit-size

sublots. Kalir and Sarin (2001) investigated equal-

size sublots and developed a bottleneck minimal

idleness heuristic to generate solutions that were

very close to the optimum. To the best of our

knowledge, the n-job model in a ﬂowshop with total

ﬂow time criterion was not considered in the

literature.

With the advent of just-in-time (JIT), the crite-

rion involving both earliness and tardiness penalties

has received signiﬁcant attention. Yoon and Ven-

tura (2002a) examined lot-streaming ﬂowshop

scheduling with respect to earliness and tardiness

penalties. For a given job sequence, they presented

linear programming (LP) models to obtain the opti-

mal sublot allocation for cases where the buﬀers

between successive machines have limited or inﬁnite

capacities and the sublots have equal sizes or are

consistent. For the case with equal-size sublot and

inﬁnite capacity buﬀer, sixteen pairwise interchange

methods obtained by combining four rules to gener-

ate initial sequences with four neighborhood search

mechanisms are considered. The experimental

results showed that the best performance was

obtained using a non-pairwise interchange

mechanism and the smallest overall slack time rule

to generate the initial sequence. Later, Yoon and

Ventura (2002b) provided a genetic algorithm

(GA) that incorporated the LP and pairwise inter-

change method for the lot-streaming ﬂowshop

scheduling with equal-size sublot and inﬁnite capac-

ity buﬀer. Their computational results showed that

the proposed GA, called the hybrid genetic algo-

rithm (HGA), works well for this type of problem.

Particle swarm optimization (PSO), proposed by

Kennedy and Eberhart (1995), is a novel metaheu-

ristic. To address various types of optimization

problems, both the continuous and discrete versions

of PSO have been developed (Kennedy and Eber-

hart, 1995, 1997). Since then, PSO has been success-

fully applied to many continuous and discrete

optimization problems (Kennedy and Eberhart,

1995; Van den Bergh and Engelbrecht, 2000; Clerc,

2004; Allahverdi and Al-Anzi, 2006).

The literature on PSO applied to the scheduling

problem is limited. Tasgetiren et al. (2004a,b,

2007) proposed PSO algorithms extended from the

continuous version (Kennedy and Eberhart, 1995).

They used the smallest position value (SPV) rule,

borrowed from the random key representation of

GA, to conv ert the continuous position values into

a discrete job sequence. Their PSO algorithms with

local search were eﬀectively applied to solve single

machine and ﬂowshop scheduling problems. On

the other hand, two discrete PSO (DPSO) algo-

rithms exist in the literature for solving ﬂowshop

scheduling problems. Rameshkumar et al. (2005)

proposed a DPSO algorithm where new operations

based on job transpositions are provided to com-

pute particle velocity and update particle positions.

Liao et al. (2007) also developed a DPSO algorithm

based on the discrete PSO version (Kennedy and

Eberhart, 1997 ). In their DPSO algorithm, the par-

ticle and the velocity are redeﬁned and an eﬃcient

approach is developed to move a particle to the

new job sequence.

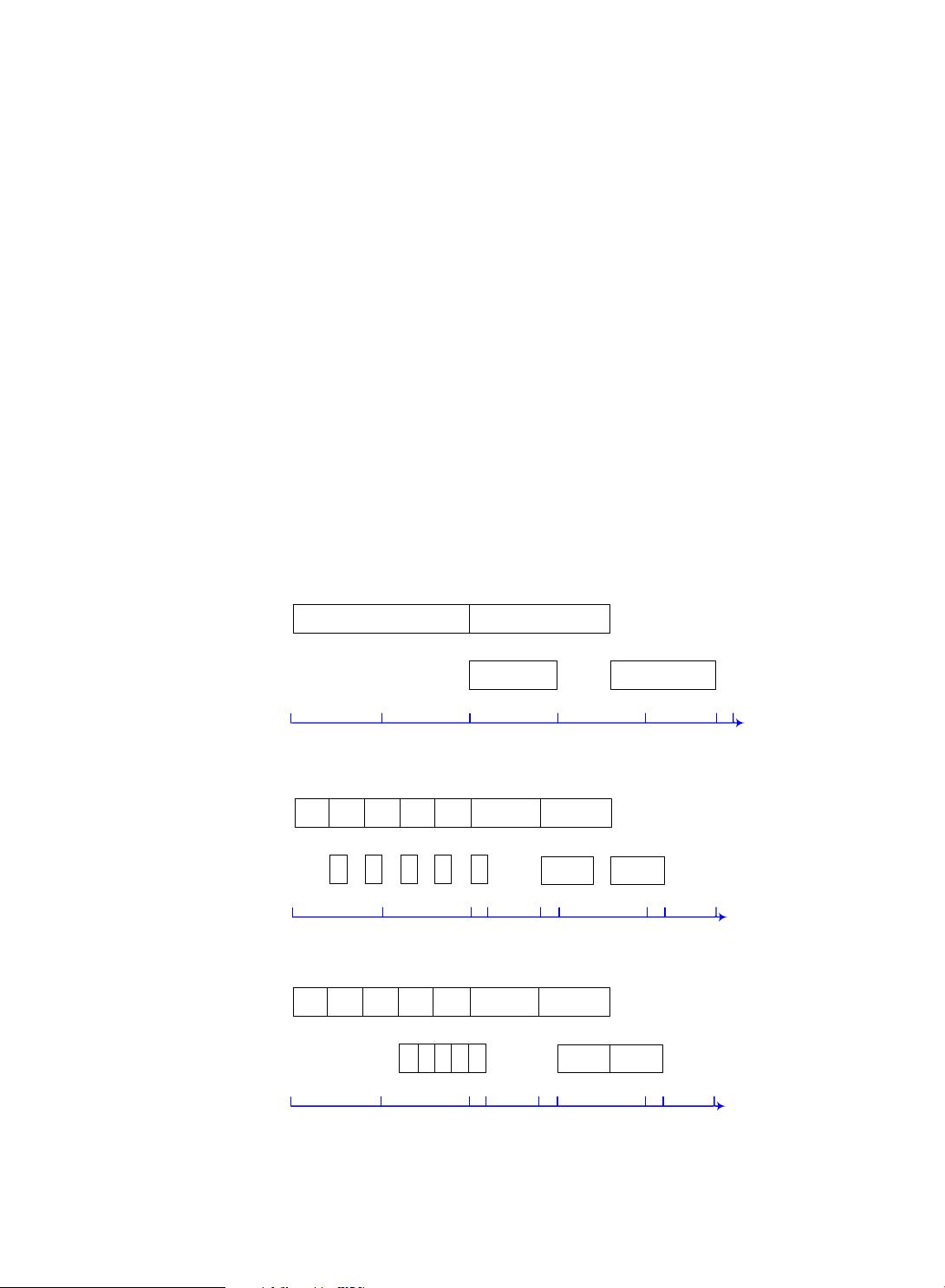
In this paper, we address the lot-stre aming ﬂow-

shop scheduling problem with the objective of min-

imizing the total weighted earliness and tardiness.

As in Yoon and Ventura (2002b), we assume

equal-size sublots and inﬁnite capacity buﬀers. Tri-

etsch and Baker (1993)

reviewed three types of sub-

lots including equal-size, consistent and variable

sublots. They indicated that it may be more attrac-

tive to use equal-size sublots in some applications,

such as an application described by Kalir and Sarin

(2001) for scheduling surface mount technology

(SMT) ﬂow line.

C.-T. Tseng, C.-J. Liao / European Journal of Operational Research 191 (2008) 360–373 361

The problem solving process is separated into

two phases. In the ﬁrst phase, we provide a so-called

net beneﬁt of movement (NBM) algorithm to deter-

mine the optimal sublot allocation for a given

sequence. The NBM algorithm is much more eﬃ-

cient than the LP model by Yoon and Ventura

(2002b). In the second phase, we propose a discrete

PSO (DPSO) algorithm to ﬁnd the best sequence.

The proposed DPSO will be compared with the

HGA of Yoon and Ventura (2002b).

2. Lot streaming in a ﬂowshop

In this section, we illustrate the beneﬁts of lot

streaming in a ﬂowshop and formally deﬁne the

addressed problem.

2.1. Importance of lot streami ng

An example of 2-job, 2-machine ﬂowshop is used

to illustrate the beneﬁts of lot streaming. Suppose

the processing times of jobs 1 and 2 on machine 1

are 10 and 8, and on machine 2 are 5 and 6, respec-

tively. Jobs 1 and 2 can be split into 5 and 2 equal-

size sublots, respectively. In a traditional ﬂowshop

as shown in Fig. 1a, the completion times for jobs

1 and 2 are 15 and 24, respectively. In a ﬂowshop

with lot streaming, the completion times for jobs 1

and 2 are reduced to 11 and 21 (see Fig. 1b), respec-

tively. Obviously, various performance measures are

improved with lot streaming. The makespan is

reduced from 24 to 21, a reduction of 12.5%; the

machine idle time is reduced from 13 to 10, a reduc-

tion of 23.1%; the total ﬂow time is reduced from 39

to 32, a reduction of 17.9%. Therefore, lot streaming

can improve the overall performance of the produc-

tion system. In practice, to reduce the setup times,

the ﬁnal schedule should delay the processing of

all sublots on each machine as much as possible

without aﬀecting the starting times of all the last

sublots on the last machine. Thus, the ﬁnal schedule

for the example is as shown in Fig. 1c.

Machine 1

Machine 2

510152024

1 2

Machine 1

Machine 2

10 15 20 21

21111 2

1411

(a) schedule without sublots

(b) schedule with sublots

Machine 1

Machine 2

510152021

21111 2

1111

1411

Fig. 1. Schedules for the example without and with sublots in a ﬂowshop.

362 C.-T. Tseng, C.-J. Liao / European Journal of Operational Research 191 (2008) 360–373

剩余13页未读，继续阅读

评论收藏

内容反馈

qq_21435923

粉丝: 0
资源: 1

A discrete particle swarm optimization

A conflict-congestion model for pedestrian-vehicle mixed evacuation based on discrete particle swarm optimization algorithm

Discrete particle swarm optimization based on estimation of distribution for terminal assignment problems

particle swarm optimization

Fractional-order particle swarm optimization

A heuristic particle swarm optimization.pdf

A non-revisiting particle swarm optimization.pdf

Discrete Particle Swarm Optimization Based Antenna Selection for MIMO LoRa IoT Systems

求解TSP问题的混合离散粒子群算法.pdf

论文研究-基于模糊随机规划的反TBM目标分配优化模型.pdf

Design of particle swarm optimization with random flying time

Modification of particle swarm optimization with human simulated property

Yu 等。 - 2014 - An improved quantum particle swarm optimization a

Improved particle swarm optimization combined with chaos

Fuzzy-multi-objective particle swarm optimization

基于交叉算子和邻域搜索算子的离散粒子群优化算法.pdf

自适应变异的离散粒子群算法研究.pdf

改进离散粒子群算法在冷负荷启动的配电网馈线恢复中的应用.pdf

多信息结合离散粒子群算法及其应用.pdf

多目标粒子群社团检测算法MODPSO

ypea102-particle-swarm-optimization.zip_AI CODE_swarm

Example-based learning particle swarm optimization for continuous optimization

Apical-dominant particle swarm optimization

A dynamic inertia weight particle swarm optimization algorithm

A co-evolving framework for robust particle swarm optimization

最新资源