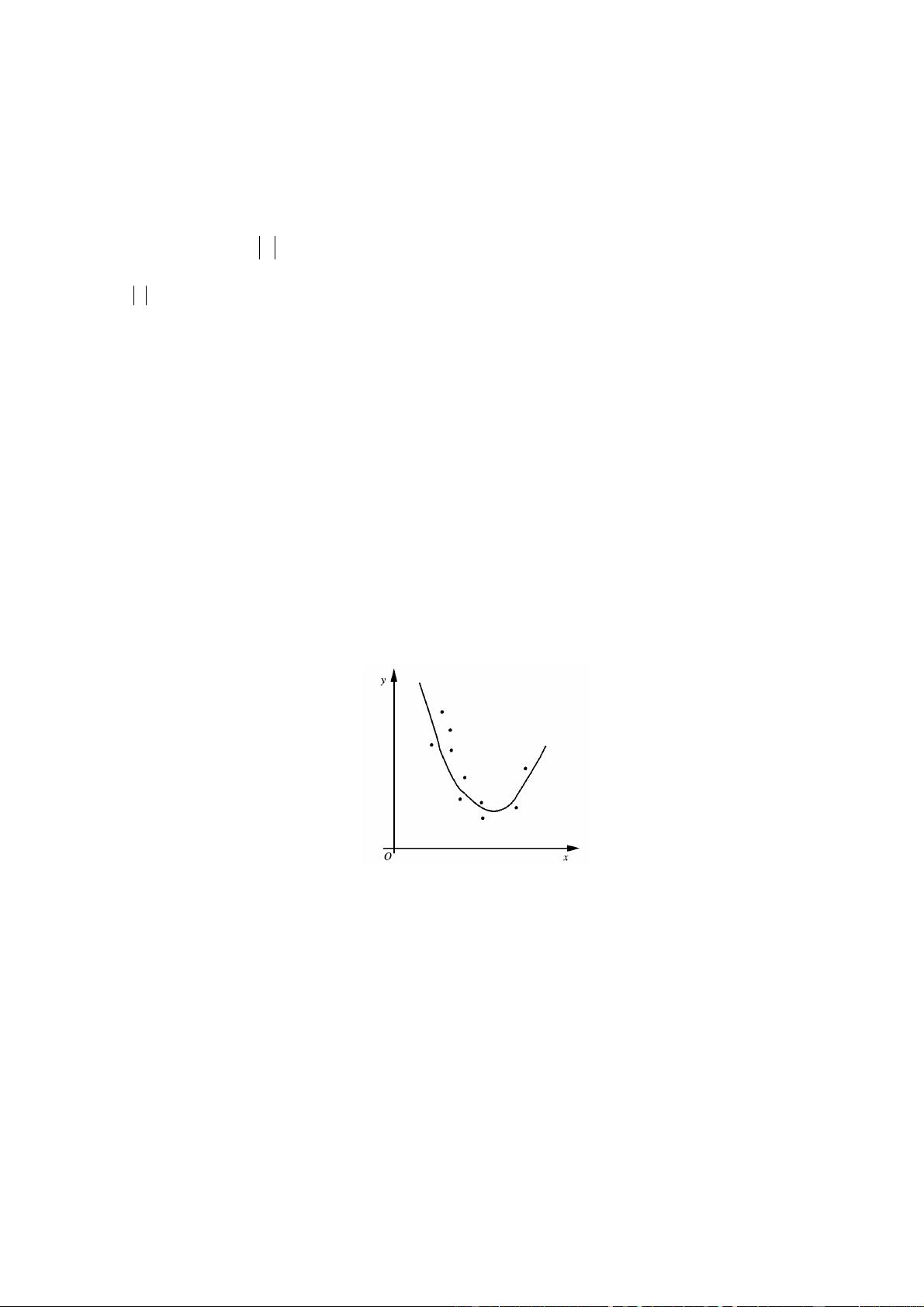
最小二乘法的基本原理和多项式拟合

### 最小二乘法的基本原理和多项式拟合 #### 一、最小二乘法的基本原理 最小二乘法是一种广泛应用于数据拟合的技术，它主要用于寻找一条最佳拟合线或者曲线来逼近一组数据点。这种方法的核心思想在于通过最小化误差的平方和来找到最优解。这里将详细阐述最小二乘法的基本原理以及它在多项式拟合中的应用。 对于给定的数据点 \((x_i, y_i)\)，\(i = 0, 1, \ldots, m\)，我们的目标是找到一个函数 \(p(x)\)，使得该函数与这些数据点之间的“距离”尽可能小。这个“距离”可以通过多种方式定义，其中最常用的是误差平方和。具体来说，我们希望找到一个函数 \(p(x)\)，使得下面的目标函数最小： \[ S(p) = \sum_{i=0}^{m} (y_i - p(x_i))^2 \] 这里，\(S(p)\) 表示误差平方和。为了实现这一目标，我们需要在预设的函数类 \(\Phi\) 中选择合适的函数形式 \(p(x)\)。 #### 二、误差衡量方法 在寻找最佳拟合函数的过程中，通常会考虑几种不同的误差衡量方法。这些方法包括： 1. **误差绝对值的最大值**：即所有数据点的误差绝对值中的最大值。数学上表示为 \(\max_{0 \leq i \leq m} |y_i - p(x_i)|\)。 2. **误差绝对值的和**：所有数据点的误差绝对值之和，表示为 \(\sum_{i=0}^{m} |y_i - p(x_i)|\)。 3. **误差平方和**：所有数据点的误差平方之和，表示为 \(\sum_{i=0}^{m} (y_i - p(x_i))^2\)。 前三者中，误差平方和由于便于进行微分运算而被广泛使用。特别是在曲线拟合问题中，我们通常会选择最小化误差平方和的方式来确定最佳拟合函数。 #### 三、多项式拟合 在实际应用中，多项式拟合是非常常见的一种情况。当我们选择多项式作为拟合函数时，问题变成了寻找一个次数不超过 \(n\) 的多项式 \(p_n(x) = \sum_{k=0}^{n} a_k x^k\)，使得误差平方和最小。这里，\(n\) 是预先设定的多项式的最高次幂。 为了求解这个问题，我们首先定义误差平方和 \(S(p_n)\) 为： \[ S(p_n) = \sum_{i=0}^{m} (y_i - p_n(x_i))^2 = \sum_{i=0}^{m} \left(y_i - \sum_{k=0}^{n} a_k x_i^k\right)^2 \] 为了使 \(S(p_n)\) 达到最小值，我们需要对 \(S(p_n)\) 关于每个参数 \(a_0, a_1, \ldots, a_n\) 求偏导数，并令它们等于零，得到正规方程组： \[ \begin{aligned} \frac{\partial S}{\partial a_j} &= -2 \sum_{i=0}^{m} x_i^j (y_i - p_n(x_i)) = 0, \\ &\quad j = 0, 1, \ldots, n \end{aligned} \] 通过解这个正规方程组，我们可以找到系数 \(a_0, a_1, \ldots, a_n\) 的最优解，从而得到最小二乘拟合多项式 \(p_n(x)\)。 #### 四、正规方程组的求解 正规方程组可以通过矩阵的形式表示为： \[ \begin{bmatrix} \sum_{i=0}^{m} x_i^0 & \sum_{i=0}^{m} x_i^1 & \cdots & \sum_{i=0}^{m} x_i^n \\ \sum_{i=0}^{m} x_i^1 & \sum_{i=0}^{m} x_i^2 & \cdots & \sum_{i=0}^{m} x_i^{n+1} \\ \vdots & \vdots & \ddots & \vdots \\ \sum_{i=0}^{m} x_i^n & \sum_{i=0}^{m} x_i^{n+1} & \cdots & \sum_{i=0}^{m} x_i^{2n} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_n \end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{m} y_i x_i^0 \\ \sum_{i=0}^{m} y_i x_i^1 \\ \vdots \\ \sum_{i=0}^{m} y_i x_i^n \end{bmatrix} \] 这个矩阵方程可以写作 \(\mathbf{A}\mathbf{a} = \mathbf{b}\)，其中 \(\mathbf{A}\) 是系数矩阵，\(\mathbf{a}\) 是未知系数向量，\(\mathbf{b}\) 是右侧向量。系数矩阵 \(\mathbf{A}\) 是一个对称正定矩阵，这意味着正规方程组总是有唯一解。通过求解这个方程组，我们可以找到多项式拟合的最佳参数。 #### 结论 通过以上讨论可以看出，最小二乘法提供了一种系统的方法来解决数据拟合问题。无论是简单的线性拟合还是复杂的高阶多项式拟合，最小二乘法都能够有效地处理。此外，通过正规方程组的求解，我们可以精确地找到最小二乘拟合多项式，从而获得最佳的数据拟合结果。这种技术在工程、科学、经济学等多个领域都有广泛的应用。