
INSTRUCTOR'S SOLUTIONS MANUAL

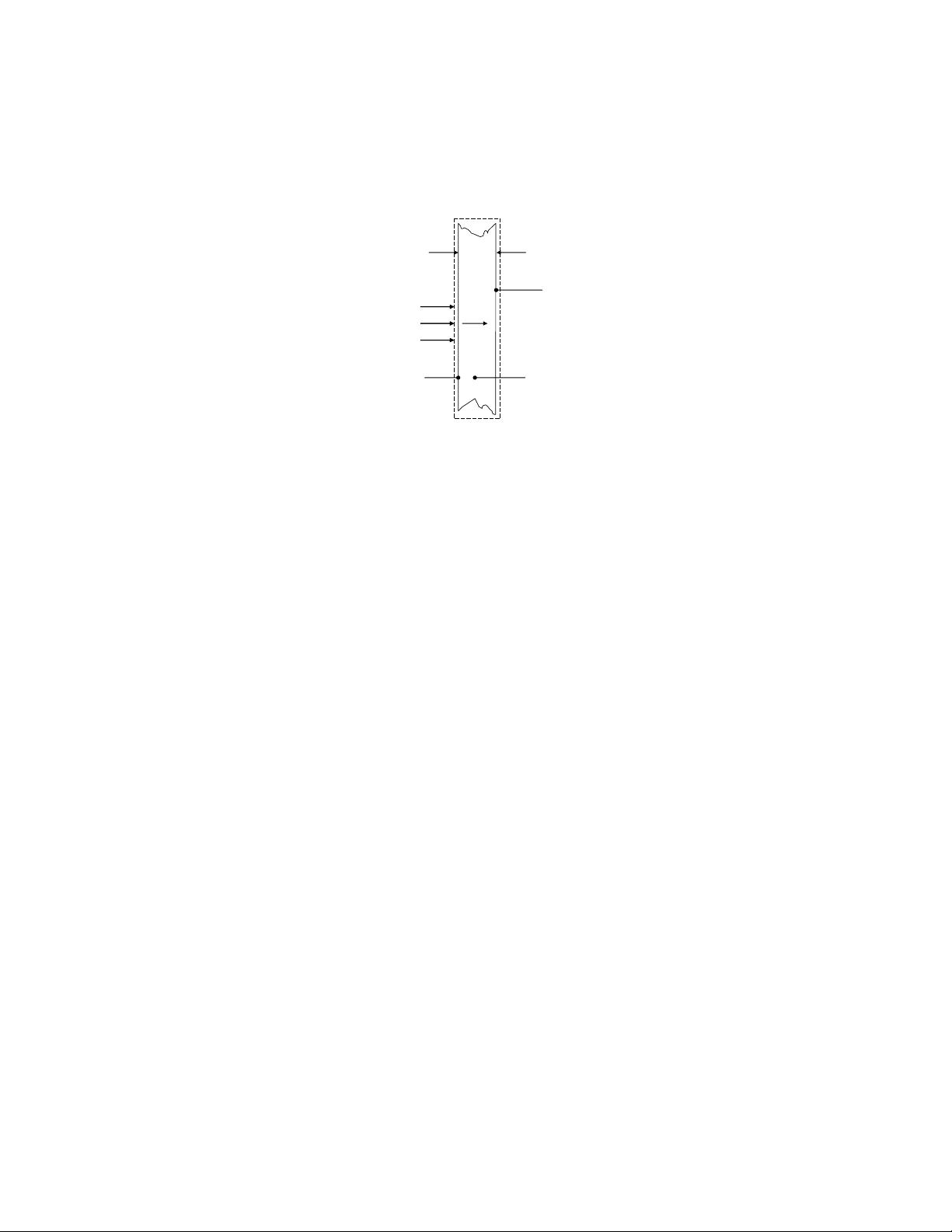
PROBLEM 1.1
KNOWN: Thermal conductivity, thickness and temperature difference across a sheet of rigid
extruded insulation.
FIND: (a) The heat flux through a 2 m × 2 m sheet of the insulation, and (b) The heat rate
through the sheet.
SCHEMATIC:
ASSUMPTIONS: (1) One-dimensional conduction in the x-direction, (2) Steady-state
conditions, (3) Constant properties.
ANALYSIS: From Equation 1.2 the heat flux is
12
x
T - T
dT
q = -k = k
dx L
′′
Solving,
"
x
W 10 K
q = 0.029 ×
m K 0.02 m⋅
x
2
W
q = 14.5
m
′′
<
The heat rate is
2
xx
2
W
q = q A = 14.5 × 4 m = 58 W
m
′′
⋅
<
COMMENTS: (1) Be sure to keep in mind the important distinction between the heat flux
(W/m
2
) and the heat rate (W). (2) The direction of heat flow is from hot to cold. (3) Note that
a temperature
difference may be expressed in kelvins or degrees Celsius.
q
cond
A = 4 m
2
T
2
T
1
k = 0.029
⋅
W
mK
x
L = 20 mm
T
1
–T
2
= 10˚C
q
cond
A = 4 m
2
T
2
T
1
k = 0.029
⋅
W
mK
x
L = 20 mm
T
1
–T
2
= 10˚C
PROBLEM 1.2
KNOWN: Thickness and thermal conductivity of a wall. Heat flux applied to one face and
temperatures of both surfaces.
FIND: Whether steady-state conditions exist.
SCHEMATIC:
ASSUMPTIONS: (1) One-dimensional conduction, (2) Constant properties, (3) No internal energy
generation.
ANALYSIS: Under steady-state conditions an energy balance on the control volume shown is
2
in out cond 1 2
( )/ 12 W/m K(50 C 30 C)/0.01 m 24,000 W/mqq q kTTL
′′ ′′ ′′
== =− = ⋅ °−° =
Since the heat flux in at the left face is only 20 W/m
2
, the conditions are not steady state. <
COMMENTS: If the same heat flux is maintained until steady-state conditions are reached, the
steady-state temperature difference across the wall will be
ΔT =
2
/ 20 W/m 0.01 m/12 W/m K 0.0167 KqL k
′′
=× ⋅=
which is much smaller than the specified temperature difference of 20
°C.
q”= 20 W/m
2
L = 10 mm
k = 12 W/m·K
T
1
= 50°C
T
2
= 30°C
q″
cond
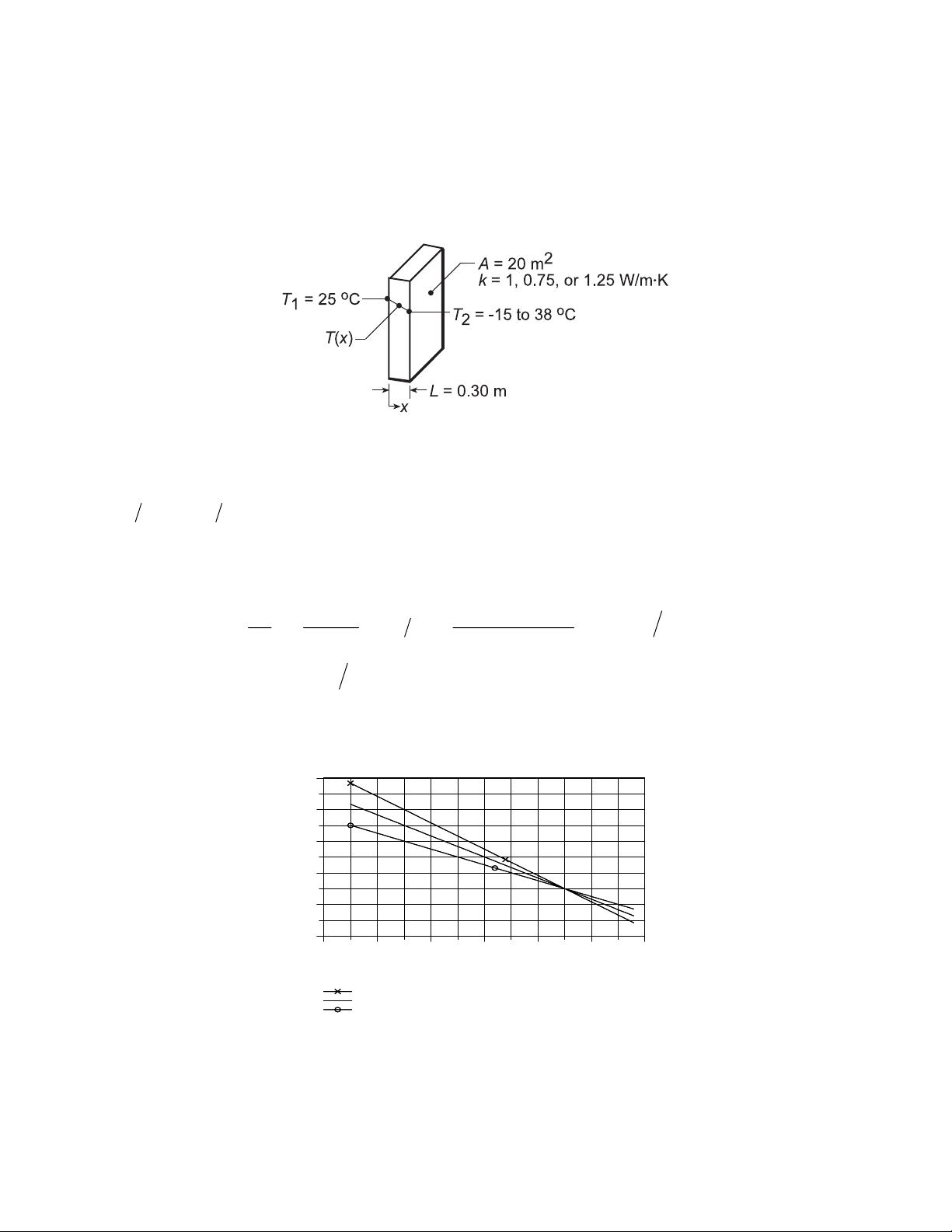
PROBLEM 1.3
KNOWN: Inner surface temperature and thermal conductivity of a concrete wall.
FIND: Heat loss by conduction through the wall as a function of outer surface temperatures ranging from
-15 to 38°C.
SCHEMATIC:
ASSUMPTIONS: (1) One-dimensional conduction in the x-direction, (2) Steady-state conditions, (3)
Constant properties.
ANALYSIS: From Fourier’s law, if
x
q
′′
and k are each constant it is evident that the gradient,
x
dT dx q k
′′
=− , is a constant, and hence the temperature distribution is linear. The heat flux must be
constant under one-dimensional, steady-state conditions; and k is approximately constant if it depends
only weakly on temperature. The heat flux and heat rate when the outside wall temperature is T
2
= -15°C
are
(
)
2
12
x
25 C 15 C
dT T T
q k k 1W m K 133.3W m
dx L 0.30m
−−
−
′′
=− = = ⋅ =
oo
. (1)
22
xx
q q A 133.3W m 20m 2667W
′′
=×= × = . (2) <
Combining Eqs. (1) and (2), the heat rate q
x
can be determined for the range of outer surface temperature,
-15
≤ T
2
≤ 38°C, with different wall thermal conductivities, k.
For the concrete wall, k = 1 W/m
⋅K, the heat loss varies linearly from +2667 W to -867 W and is zero
when the inside and outer surface temperatures are the same. The magnitude of the heat rate increases
with increasing thermal conductivity.
COMMENTS: Without steady-state conditions and constant k, the temperature distribution in a plane
wall would not be linear.
-20 -10 0 10 20 30 40
Ambient air temperature, T2 (C)
-1500
-500
500
1500
2500
3500
Heat loss, qx (W)
Wall thermal conductivity, k = 1.25 W/m.K
k = 1 W/m.K, concrete wall
k = 0.75 W/m.K
Outside surface
-20 -10 0 10 20 30 40
Ambient air temperature, T2 (C)
-1500
-500
500
1500
2500
3500
Heat loss, qx (W)
Wall thermal conductivity, k = 1.25 W/m.K
k = 1 W/m.K, concrete wall
k = 0.75 W/m.K
Outside surface
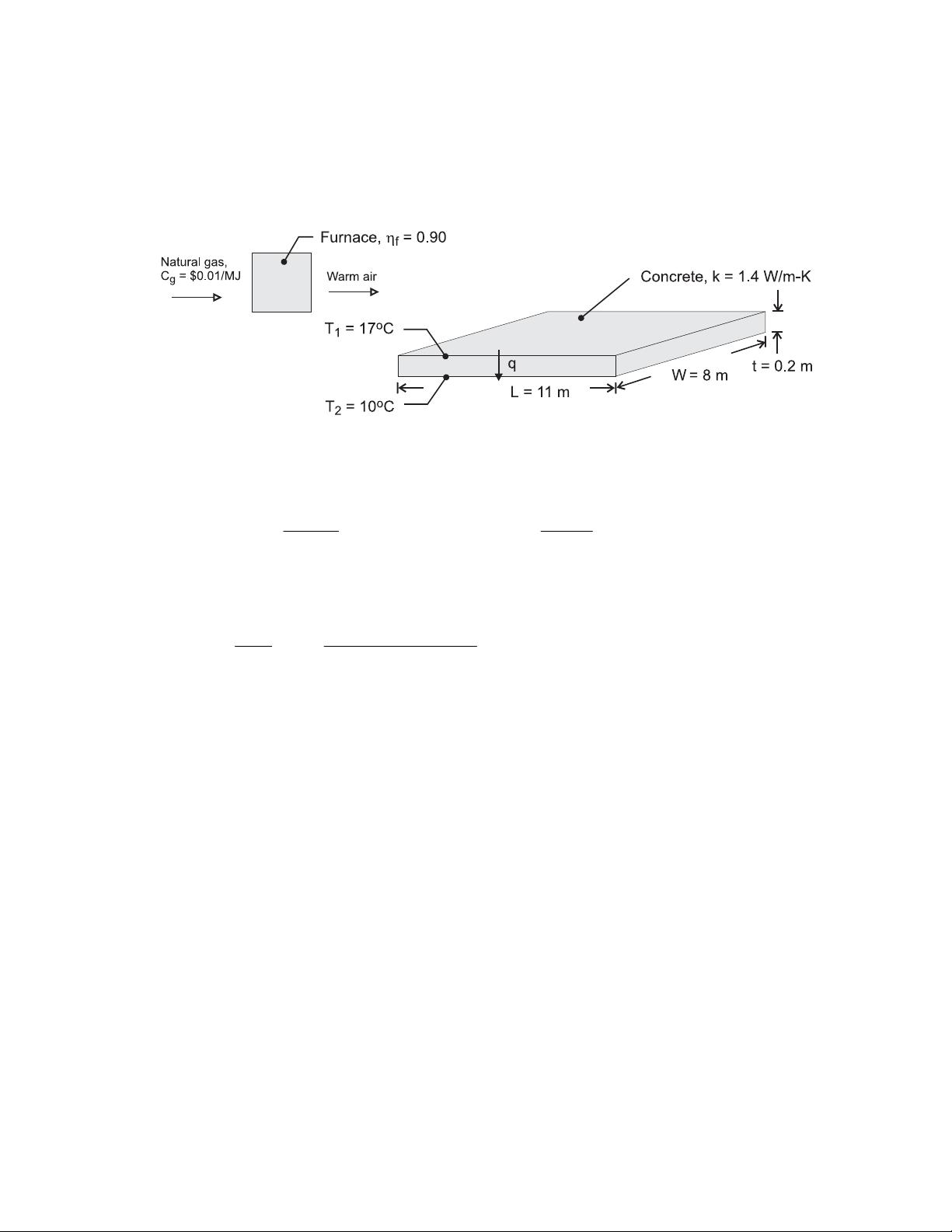
PROBLEM 1.4
KNOWN: Dimensions, thermal conductivity and surface temperatures of a concrete slab. Efficiency
of gas furnace and cost of natural gas.
FIND: Daily cost of heat loss.
SCHEMATIC:
ASSUMPTIONS: (1) Steady state, (2) One-dimensional conduction, (3) Constant properties.
ANALYSIS: The rate of heat loss by conduction through the slab is
() ()
12
TT 7C
q k LW 1.4W / m K 11m 8m 4312 W
t0.20m
−°
==⋅×=
<
The daily cost of natural gas that must be combusted to compensate for the heat loss is
() ()
g
d
6
f
qC
4312W $0.02/ MJ
C t 24h/d 3600s / h $8.28/d
0.9 10 J / MJ
η
×
=Δ= × =
×
<
COMMENTS: The loss could be reduced by installing a floor covering with a layer of insulation
between it and the concrete.















- 1
- 2
前往页