### 一阶系统及二阶系统时域特性MatLab仿真实验报告
#### 实验目的
本实验旨在通过具体的系统设计及理论分析方法,帮助学生深入理解自动控制系统的设计与分析方法,并熟悉Matlab这一仿真分析工具。具体目标包括:
1. **加深对自动控制系统设计与分析方法的理解**:通过实验操作让学生能够直观地看到理论知识在实际中的应用。
2. **熟练掌握Matlab软件**:学习如何利用Matlab进行系统建模和仿真,以便于更好地理解和分析系统行为。
3. **一阶系统时域特性研究**:掌握一阶系统的时域特性,并理解时间常数T对系统性能的具体影响。
4. **二阶系统时域特性探究**:掌握二阶系统的时域特性,并探究不同参数(如阻尼比ξ)变化对系统性能的影响。
#### 实验设备
本次实验所需设备包括:
- **计算机**:用于运行Matlab软件进行仿真分析。
- **Matlab仿真软件**:作为主要的仿真工具。
#### 实验内容
本实验分为两个主要部分:一阶系统时域特性的研究与二阶系统时域特性的研究。
1. **一阶系统时域特性**
- **系统模型**:采用一阶系统模型\[ G(s) = \frac{1}{1 + Ts} \],其中\(T\)为时间常数。
- **仿真内容**:通过改变时间常数\(T\)的值(例如0.4、1.2、2.0、2.8、3.6、4.4),观察并分析不同\(T\)值下系统对单位阶跃输入的响应情况。
2. **二阶系统时域特性**
- **二阶线性系统模型**:采用模型\[ G(s) = \frac{16}{s^2 + 4s + 16} \],分析系统的单位脉冲响应、单位阶跃响应以及单位正弦输入响应。
- **微分负反馈位置随动系统**:基于该系统模型,计算不同微分反馈时间常数τ(0、0.0125、0.025)下的系统响应性能指标(如上升时间、峰值时间等)。
- **阻尼比ξ对系统响应的影响**:对于二阶系统\[ G(s) = \frac{36}{s^2 + 12s + 36} \],当阻尼比ξ分别为0.1、0.2、0.5、0.7、1.0、2.0时,仿真单位阶跃响应并分析ξ值的变化如何影响系统的响应性能。
#### 实验要求
- 学生需严格遵守实验室规定,独立完成实验内容。
- 在实验过程中遇到问题时,应尝试独立解决,在教师指导下逐步分析和解决问题。
- 完成相关实验后,记录实验程序、响应曲线及性能指标,并进行实验结果的比较与分析。
- 分析系统的动态特性,包括但不限于响应速度、稳定性等方面。
- 撰写详细的实验报告并按时提交。
#### Matlab编程仿真与实验分析示例
**一阶系统时域特性**
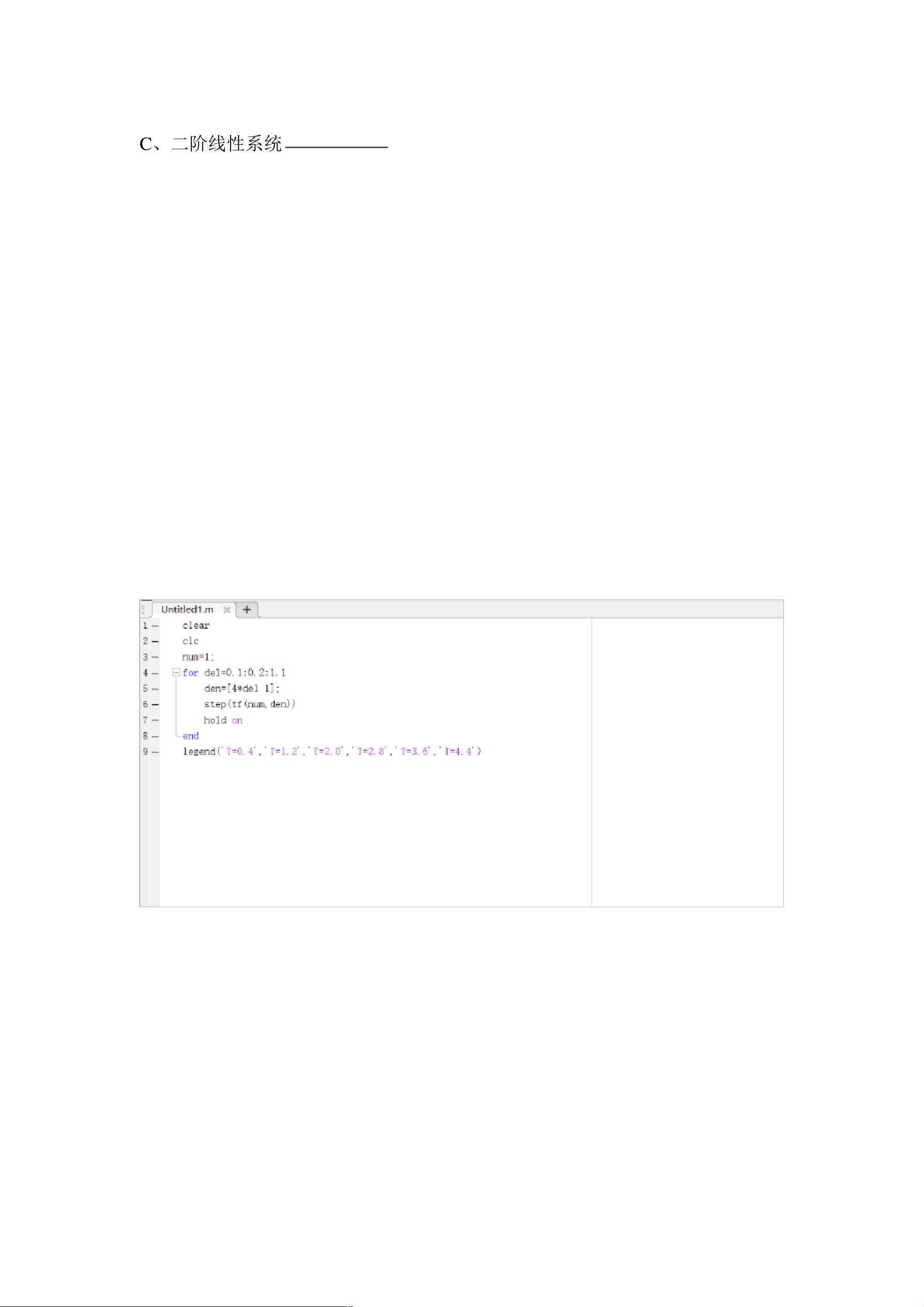
**实验代码**:假设使用了以下代码进行仿真分析:
```matlab
% 设置时间常数T
T_values = [0.4 1.2 2.0 2.8 3.6 4.4];
for i = 1:length(T_values)
T = T_values(i);
num = 1;
den = [T 1];
sys = tf(num, den); % 创建系统模型
step(sys); % 绘制单位阶跃响应
hold on; % 保持图形
end
legend('T=0.4','T=1.2','T=2.0','T=2.8','T=3.6','T=4.4');
title('一阶系统单位阶跃响应');
xlabel('时间 (秒)');
ylabel('响应');
```
**运行曲线**:(此处未提供实际图表)
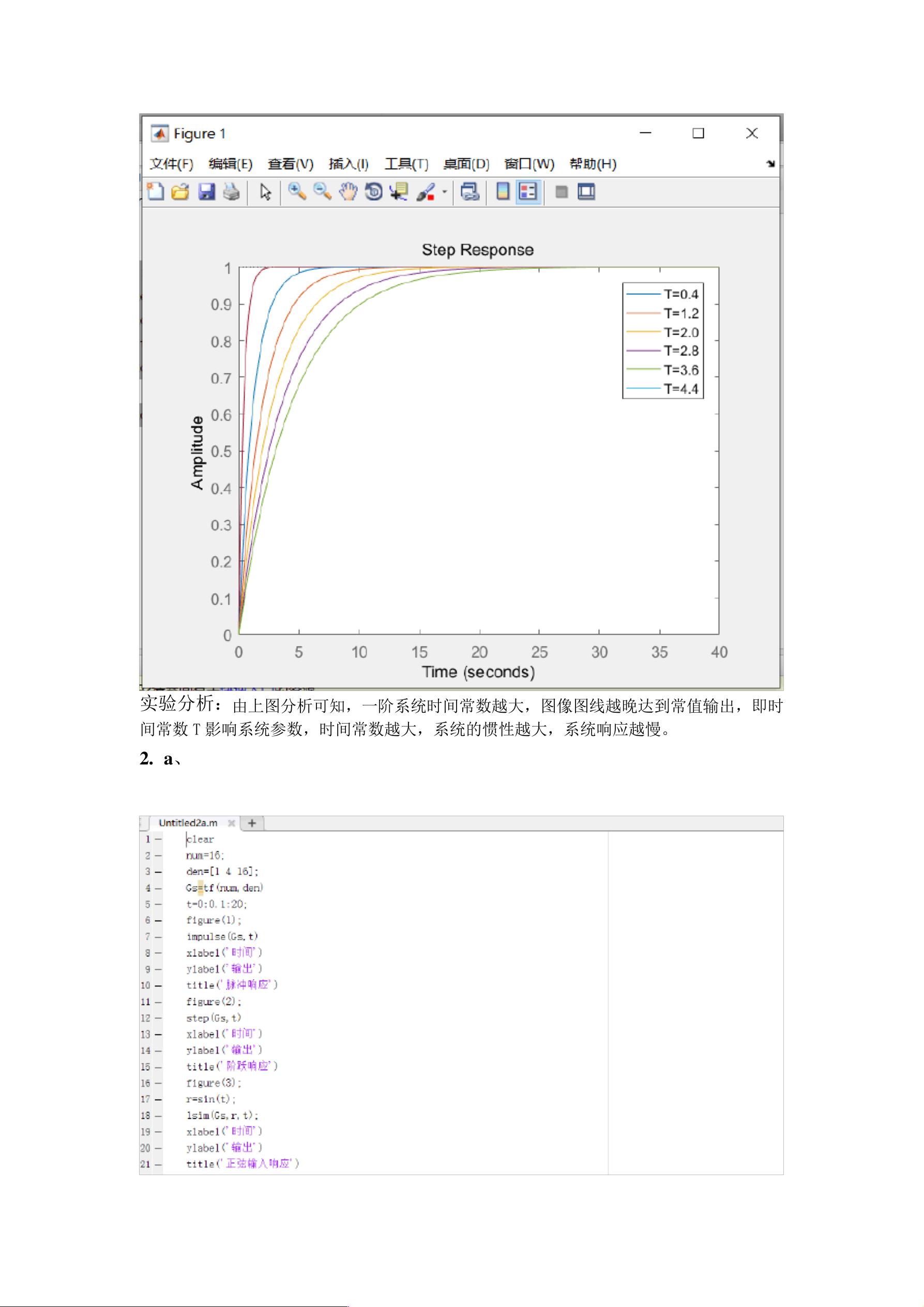
**实验分析**:通过观察不同时间常数\(T\)下的一阶系统单位阶跃响应曲线,可以明显看出,随着\(T\)值的增加,系统响应变得更加缓慢,即达到稳态的时间更长。这表明时间常数\(T\)对系统性能有直接影响,时间常数越大,系统的惯性越大,响应越慢。
**二阶系统时域特性**
**2.a 实验代码**:假设使用了以下代码进行仿真分析:
```matlab
num = 16;
den = [1 4 16];
sys = tf(num, den);
subplot(3,1,1);
impulse(sys); % 单位脉冲响应
subplot(3,1,2);
step(sys); % 单位阶跃响应
subplot(3,1,3);
lsim(sys, sin([0:0.1:10])); % 单位正弦输入响应
```
**运行曲线**:(此处未提供实际图表)
**实验分析**:从单位脉冲响应和单位阶跃响应的仿真结果可以看出,二阶系统的响应表现为衰减振荡的形式。而对于单位正弦输入响应,则显示了输出信号相对于输入信号的相位滞后现象。
**2.c 实验代码**:假设使用了以下代码进行仿真分析:
```matlab
% 阻尼比ξ的取值
xi_values = [0.1 0.2 0.5 0.7 1.0 2.0];
for i = 1:length(xi_values)
xi = xi_values(i);
num = 36;
den = [1 12*xi 36];
sys = tf(num, den);
step(sys);
hold on;
end
legend('ξ=0.1','ξ=0.2','ξ=0.5','ξ=0.7','ξ=1.0','ξ=2.0');
title('二阶系统单位阶跃响应');
xlabel('时间 (秒)');
ylabel('响应');
```
**运行曲线**:(此处未提供实际图表)
**实验分析**:通过对不同阻尼比ξ值下二阶系统单位阶跃响应的观察,我们可以得出以下结论:当ξ小于1时(欠阻尼状态),系统响应呈现出明显的振荡特性;当ξ等于1时(临界阻尼状态),响应表现为较快的非振荡形式;而当ξ大于1时(过阻尼状态),虽然响应同样是非振荡的,但达到稳态的时间更长。这些分析结果有助于我们深入了解阻尼比ξ对二阶系统性能的具体影响。