粒子滤波用于视觉跟踪资源-CSDN文库

需积分: 9 29 浏览量 2010-10-06 15:51:44 上传评论收藏 405KB PDF 举报

### 粒子滤波在视觉跟踪中的应用与解析 #### 一、粒子滤波：超越卡尔曼滤波的新范式粒子滤波作为一种非线性动态系统状态估计的算法，近年来在计算机视觉领域，特别是在视觉跟踪技术中，展现出了其独特的优势。与经典的卡尔曼滤波方法相比，粒子滤波能够处理更复杂、更动态的场景，尤其在视觉跟踪方面，它能够有效应对多模态分布、非高斯噪声以及非线性系统模型所带来的挑战。 #### 二、粒子滤波原理概览粒子滤波的基本思想是通过一组随机样本（即“粒子”）来近似表示概率密度函数。这些粒子代表了对系统状态的可能假设，每个粒子都有一个权重，用以表示该粒子在总体分布中的相对重要性。随着系统的演化，粒子的位置会根据观测数据进行更新，而权重则反映了粒子假设与实际观测的一致性。这一过程通常包括预测、观测更新以及重采样三个步骤，确保粒子集能够准确反映当前状态的概率分布。 #### 三、视觉跟踪中的粒子滤波应用在视觉跟踪中，粒子滤波的应用主要体现在对目标物体的轮廓、特征或整体形态进行实时追踪上。相较于卡尔曼滤波，粒子滤波在处理密集视觉杂波环境下的曲线跟踪问题时更具优势。它能够处理多模态的不确定性，即使在背景中存在与目标相似的物体（如伪装或拥挤场景），粒子滤波仍能通过学习动态模型结合视觉观测，保持对目标的稳定追踪。 #### 四、算法运行机制粒子滤波的运行机制基于“条件密度传播”（CONDENSATION），这是由Michael Isard和Andrew Blake在1998年发表的论文中提出的。该算法利用随机生成的粒子集合来表示可能的解释分布，并随着时间的推移，借助学习到的动力学模型和视觉观察，更新这个粒子集合。这种方法不仅能够应对高度动态的运动，而且尽管采用了随机采样技术，仍能够在接近实时的速度下运行，展现出极高的鲁棒性。 #### 五、模型设计与通用性为了在视觉跟踪中有效地消除不确定性，粒子滤波算法设计了对形状和运动的建模方式。这些模型既具有一定的特异性，能够有效地对目标进行区分和定位，同时又具有足够的泛化能力，适用于广泛的目标类别。例如，在人群密集的场景中追踪个体，或者在复杂自然环境中识别特定动物，粒子滤波都能提供有效的解决方案。 #### 六、结论粒子滤波作为一项先进的状态估计技术，在视觉跟踪领域的应用展示了其强大的适应性和效率。通过对目标形状和运动的有效建模，粒子滤波能够克服视觉杂波带来的挑战，实现对目标的精确追踪。随着计算机硬件性能的提升和算法优化，粒子滤波在视觉跟踪中的应用将更加广泛，为智能监控、自动驾驶、机器人导航等高科技领域提供坚实的技术支持。

资源推荐

资源详情

资源评论

International Journal of Computer Vision 29(1), 5–28 (1998)

° 1998 Kluwer Academic Publishers. Manufactured in The Netherlands.

CONDENSATION—Conditional Density Propagation for Visual Tracking

MICHAEL ISARD AND ANDREW BLAKE

Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK

Received July 16, 1996; Accepted March 3, 1997

Abstract. The problem of tracking curves in dense visual clutter is challenging. Kalman ﬁltering is inadequate

because itis based on Gaussian densities which, being unimodal, cannotrepresent simultaneousalternative hypothe-

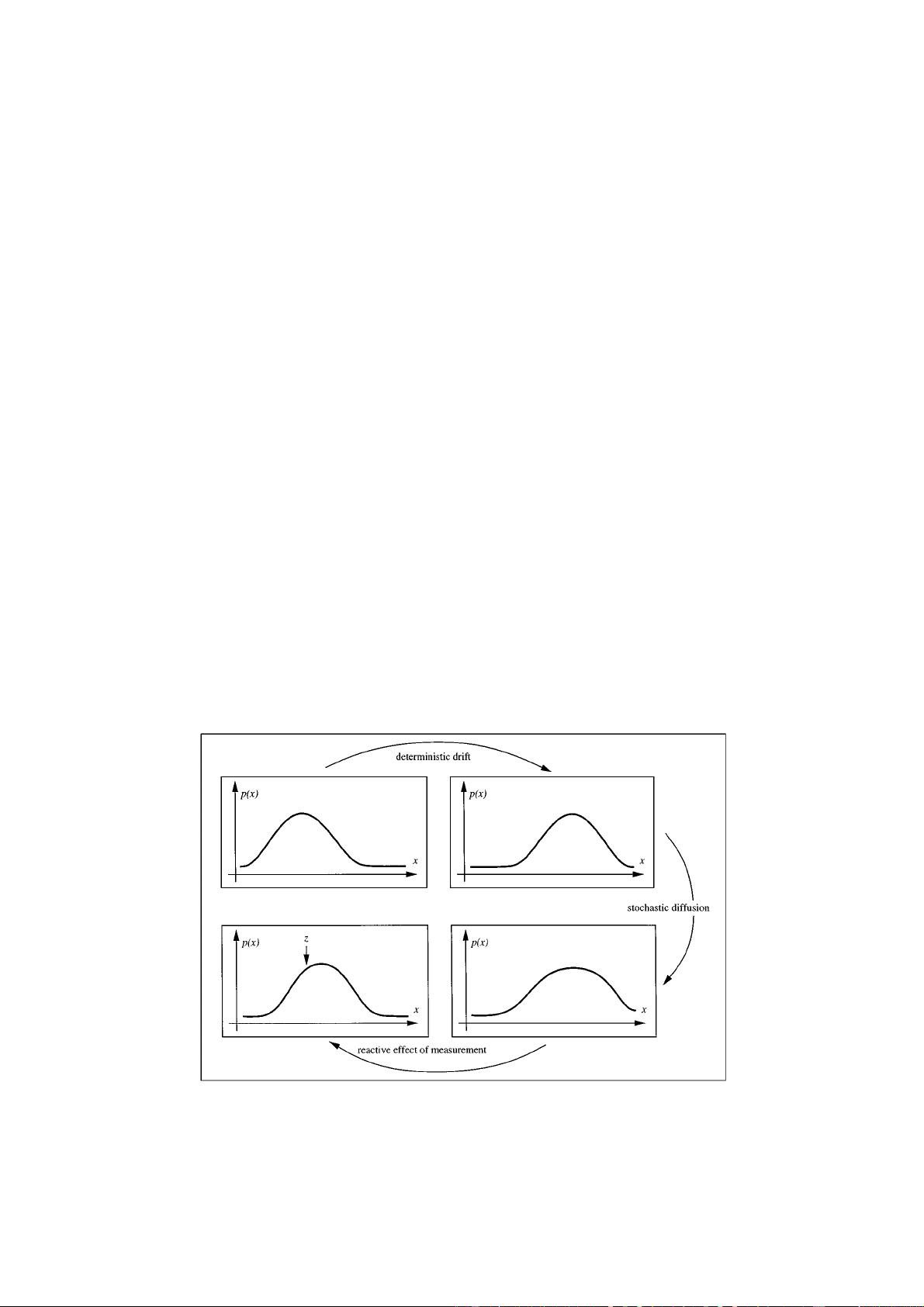
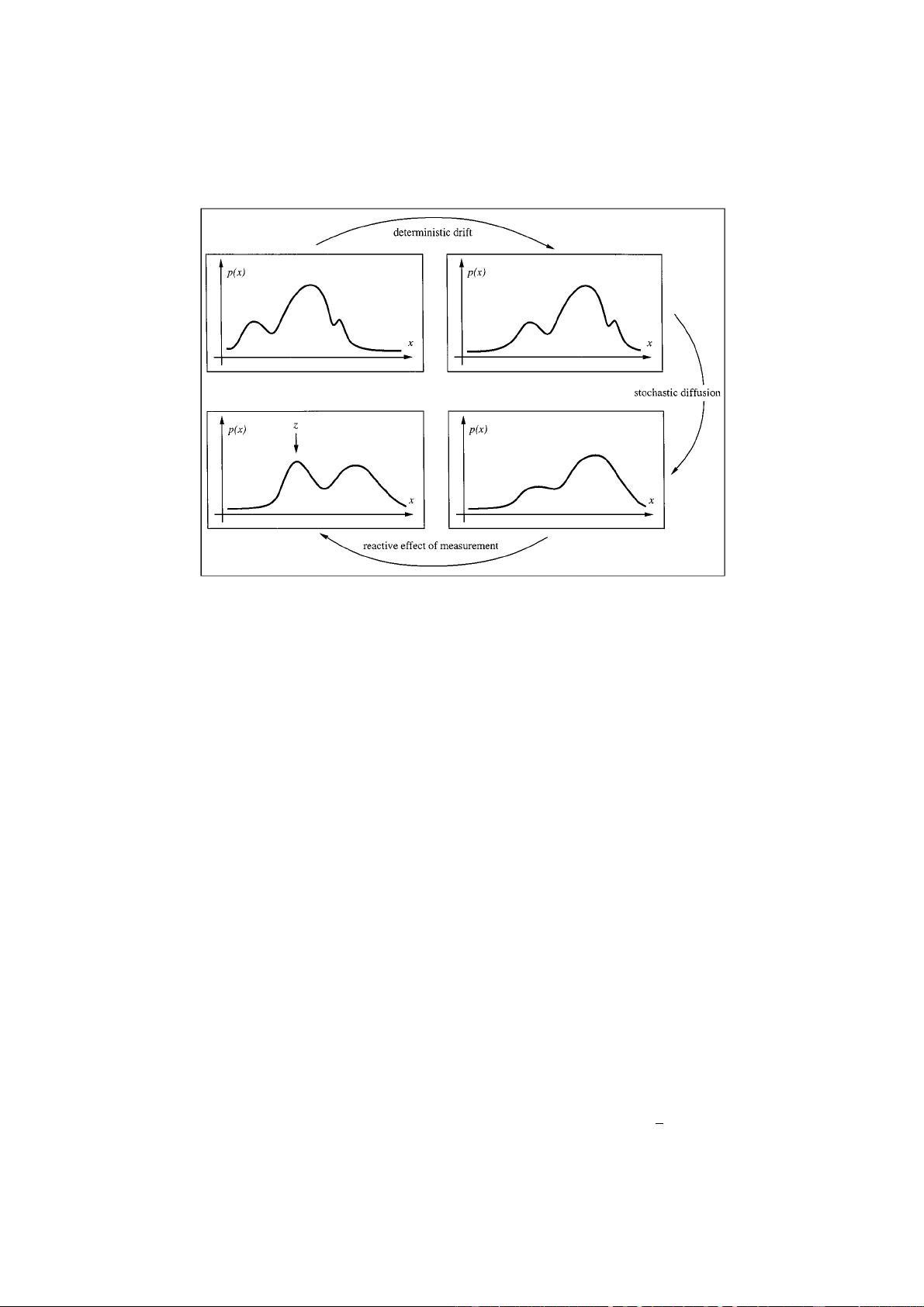
ses. The Condensation algorithm uses “factored sampling”, previously applied to the interpretation of static

images, in which the probability distribution of possible interpretations is represented by a randomly generated set.

Condensation uses learned dynamical models, together with visual observations, to propagate the random set

over time. The result is highly robust tracking of agile motion. Notwithstanding the use of stochastic methods, the

algorithm runs in near real-time.

1. Tracking Curves in Clutter

The purpose of this paper

is to establish a stochas-

tic framework for tracking curves in visual clutter, us-

ing a sampling algorithm. The approach is rooted in

ideas from statistics, control theory and computer vi-

sion. The problem is to track outlines and features of

foreground objects, modelled as curves, as they move

in substantial clutter, and to do it at, or close to, video

frame-rate. This is challenging because elements in

the background clutter may mimic parts of foreground

features. In the most severe case of camouﬂage, the

background may consist of objects similar to the fore-

ground object, for instance, when a person is moving

past a crowd. Our approach aims to dissolve the result-

ing ambiguity by applying probabilistic models of ob-

ject shapeand motionto analyse the video-stream. The

degree of generality of these models is pitched care-

fully: sufﬁciently speciﬁc for effective disambiguation

but sufﬁciently general to be broadly applicable over

entire classes of foreground objects.

1.1. Modelling Shape and Motion

Effective methods have arisen in computer vision for

modelling shape and motion. When suitable geometric

models of a moving object are available, they can be

matched effectively to image data, though usually at

considerable computational cost (Hogg, 1983; Lowe,

1991; Sullivan, 1992; Huttenlocher et al., 1993). Once

an object has been located approximately, tracking it

insubsequent images becomesmoreefﬁcientcomputa-

tionally (Lowe, 1992), especially if motion is modelled

as well as shape (Gennery, 1992; Harris, 1992). One

important facility is the modelling of curve segments

which interact with images (Fischler and Elschlager,

1973; Yuille and Hallinan, 1992) or image sequences

(Kass et al., 1987; Dickmanns, and Graefe, 1988).

This is more general than modelling entire objects but

more clutter-resistant than applying signal-processing

to low-level corners or edges. The methods to be dis-

cussed here have been applied at this level, to segments

of parametric B-spline curves (Bartels et al., 1987)

tracking over image sequences (Menet et al., 1990;

Cipolla and Blake, 1990). The B-spline curves could,

in theory, be parameterised by their control points. In

practice, this allows too many degrees of freedom for

stable tracking and it is necessary to restrict the curve

to a low-dimensional parameter x, for example, over

an afﬁne space (Koenderink and Van Doorn, 1991;

Ullman and Basri, 1991; Blake et al., 1993), or more

generally allowing a “shape-space” of non-rigid mo-

tion (Cootes et al., 1993).

6 Isard and Blake

Finally, prior probability densities can be deﬁned

over the curves (Cootes et al., 1993) represented

by appropriate parameter vectors x, and also over

their motions (Terzopoulos and Metaxas, 1991; Blake

et al., 1993), and this constitutes a powerful facility

for tracking. Reasonable defaults can be chosen for

those densities. However, it is obviously more satisfac-

tory to measure or estimate them from data-sequences

, x

,...). Algorithms todothis, assumingGaussian

densities, are known in the control-theory literature

(Goodwin and Sin, 1984) and have been applied in

computervision (Blake and Isard,1994; Baumberg and

Hogg, 1995). Given the learned prior, and an observa-

tion density that characterises the statistical variability

of image data z given a curve state x, a posterior distri-

bution can, in principle, be estimated for x

given z

successive times t.

1.2. Kalman Filters and Data-Association

Spatio-temporal estimation, the tracking of shape and

position over time, has been dealt with thoroughly by

Kalman ﬁltering, in the relatively clutter-free case in

which p(x

) cansatisfactorily be modelled asGaussian

(Dickmanns and Graefe, 1988; Harris, 1992; Gennery,

1992; Rehg and Kanade, 1994; Matthies et al., 1989)

Figure 1. Kalman ﬁlter as density propagation: in the case of Gaussian prior, process and observation densities, and assuming linear dynamics,

the propagation process of Fig. 2 reduces to a diffusing Gaussian state density, represented completely by its evolving (multivariate) mean and

variance—precisely what a Kalman ﬁlter computes.

and can be applied to curves (Terzopoulos and Szeliski,

1992; Blake et al., 1993). These solutions work rela-

tively poorly in clutter which causes the density for x

to be multi-modal and therefore non-Gaussian. With

simple, discrete featuressuch as points or corners com-

binatorial data-association methods can be effective

with clutter but combinatorial methods to do not ap-

ply naturally to curves. There remains a need for an

appropriately general probabilistic mechanism to han-

dle multi-modal density functions.

1.3. Temporal Propagation of Conditional Densities

The Kalman ﬁlter as a recursive linear estimator is a

special case, applying only to Gaussian densities, of

a more general probability density propagation pro-

cess. In continuous time this can be described in terms

of diffusion, governed by a “Fokker-Planck” equation

(Astrom, 1970), in which the density for x

drifts and

spreads under the action of a stochastic model of its

dynamics. In the simple Gaussian case, the diffusion

is purely linear and the density function evolves as

a Gaussian pulse that translates, spreads and is rein-

forced, remaining Gaussian throughout, as in Fig. 1, a

process that is described analytically and exactlyby the

Kalmanﬁlter.Therandomcomponent of the dynamical

Condensation—Conditional Density Propagation for Visual Tracking 7

Figure 2. Probability density propagation: propagation is depicted here as it occurs over a discrete time-step. There are three phases: drift due

to the deterministic component of object dynamics; diffusion due to the random component; reactive reinforcement due to observations.

model leads to spreading—increasing uncertainty—

while the deterministic component causes the density

function todrift bodily. The effect of an external obser-

vation z

is to superimpose a reactive effect on the dif-

fusion in which the density tends to peak in the vicinity

of observations. In clutter, there are typically several

competing observations and these tend to encourage a

non-Gaussian state-density (Fig. 2).

The Condensation algorithm is designed to ad-

dress this more general situation. It has the striking

propertythat, generalitynotwithstanding, itisaconsid-

erably simpler algorithm than the Kalman ﬁlter. More-

over, despite its use of random sampling which is

often thought to be computationally inefﬁcient, the

Condensation algorithm runs in near real-time.

This is because tracking over time maintains relatively

tight distributions for shape at successive time-steps,

and particularly so given the availability of accurate,

learned models of shape and motion.

2. Discrete-Time Propagation of State Density

For computational purposes, the propagation process

must be set out in terms of discrete time t. The state of

themodelledobjectat timet isdenoted x

anditshistory

is X

={x

,...,x

}. Similarly, the set of image fea-

turesat time t is z

withhistory Z

={z

,...,z

}. Note

that no functional assumptions (linearity, Gaussianity,

unimodality) are made about densities in the general

treatment, though particular choices will be made in

due course in order to demonstrate the approach.

2.1. Stochastic Dynamics

A somewhat general assumption is made for the prob-

abilistic framework that the object dynamics form a

temporal Markov chain so that

p(x

t−1

) = p(x

t−1

) (1)

—the new state is conditioned directly only on the im-

mediately preceding state, independent of the earlier

history. This still allows quite general dynamics, in-

cluding stochastic difference equations of arbitrary or-

der; we use second order models and details are given

later. The dynamics are entirely determined therefore

by the form of the conditional density p(x

t−1

).For

instance,

p(x

t−1

) ∝ exp

−

− x

t−1

− 1)

8 Isard and Blake

represents a one-dimensional random walk (discrete

diffusion) whose step length is a standard normal vari-

ate, superimposed on a rightward drift at unit speed.

Of course, for realistic problems, the state x is multi-

dimensional and the density is more complex (and, in

the applications presented later, learned from training

sequences).

2.2. Measurement

Observations z

are assumed to be independent, both

mutually and with respect to the dynamical process.

This is expressed probabilistically as follows:

p(Z

t−1

, x

t−1

) = p(x

t−1

)

t−1

i=1

p(z

). (2)

Note that integrating over x

implies the mutual condi-

tional independence of observations:

p(Z

) =

i=1

p(z

). (3)

The observation process is therefore deﬁned by speci-

fying the conditional density p(z

) at each time t,

and later, in computational examples, we take this to

be a time-independent function p(z|x). Sufﬁce it to

say for now that, in clutter, the observation density is

multi-modal. Details will be given in Section 6.

2.3. Propagation

Given a continuous-valued Markov chain with inde-

pendent observations, the conditional state-density p

at time t is deﬁned by

) ≡ p(x

This represents all information about the state at time t

that is deducible from the entire data-stream up to that

time. The rule for propagation of state density over

time is

p(x

) = k

p(z

) p(x

t−1

), (4)

where

p(x

t−1

) =

t−1

p(x

t−1

) p(x

t−1

) (5)

and k

is a normalisation constant that does not depend

on x

. The validity of therule isproved inthe appendix.

The propagation rule (4) should be interpreted sim-

ply as the equivalent of the Bayes’ rule (6) for inferring

posterior state density from data, for the time-varying

case. The effective prior p(x

t−1

) is actually a pre-

diction taken from theposterior p(x

t−1

) from the

previous time-step, onto which is superimposed one

time-step from the dynamical model (Fokker-Planck

drift plus diffusion as in Fig. 2), which is expressed in

(5). Multiplication in (4) by the observation density

p(z

) in the Bayesian manner then applies the re-

active effect expected from observations. Because the

observation density is non-Gaussian, the evolving state

density p(x

) is also generally non-Gaussian. The

problem now is how to apply a nonlinear ﬁlter to eval-

uate the state density over time, without incurring ex-

cessive computational load. Inevitably this means ap-

proximating. Numerous approaches, including“multi-

ple hypothesis tracking”, have been proposed but prove

unsuitable for use with curves as opposed to discrete

features—details are given in the appendix. In this pa-

perwe propose asamplingapproachwhich is described

in the following two sections.

3. Factored Sampling

This section describes ﬁrst the factored sampling algo-

rithm dealing withnon-Gaussian observations in single

images. Then factored sampling is extended in the fol-

lowing section to deal with temporal image sequences.

A standard problem in statistical pattern recognition

is to ﬁnd an object parameterised as x with prior p(x),

using data z from a single image. The posterior density

p(x|z) represents all the knowledge about x that is de-

ducible from the data. It can be evaluated, in principle,

by applying Bayes’ rule (Papoulis, 1990) to obtain

p(x|z) = kp(z| x)p(x) (6)

where k is a normalisation constant that is independent

of x. In cases where p(z|x) is sufﬁciently complex

that p(x |z) cannot be evaluated simply in closed form,

iterative sampling techniques can be used (Geman and

Geman, 1984; RipleyandSutherland,1990; Grenander

et al., 1991; Storvik, 1994). The factored sampling

algorithm (Grenander et al., 1991) generates a random

variatex froma distribution ˜p(x) that approximates the

posterior p(x |z). First, a sample-set {s

(1)

,...,s

(N)

}is

generated from theprior density p(x) and thenan index

剩余23页未读，继续阅读

评论收藏

内容反馈

niatzt

粉丝: 1
资源: 4

粒子滤波 用于视觉跟踪

基于粒子群优化重采样的粒子滤波用于视觉跟踪

基于粒子滤波器的视频目标跟踪

粒子滤波在图像领域的跟踪

基于粒子滤波的移动物体视觉跟踪方法 (2011年)

用粒子滤波跟踪点

高斯噪声下粒子滤波用于目标跟踪的程序

基本opencv的粒子滤波目标跟踪

MATLAB粒子滤波目标跟踪代码

用opencv粒子滤波实现的动态跟踪

粒子滤波 视频跟踪

基于粒子滤波的视觉跟踪器的设计与实现

在粒子滤波框架下使用局部约束线性编码进行视觉跟踪

基于粒子滤波的目标跟踪算法C++版

基于OPENCV实现的粒子滤波运动目标跟踪源程序

粒子滤波目标跟踪

基于DE蝙蝠算法优化粒子滤波的目标跟踪_目标跟踪_

利用粒子滤波算法进行的目标跟踪代码

粒子滤波跟踪方法研究

综合颜色和小波纹理特征的免疫粒子滤波视觉跟踪 (2011年)

使用Insect Vision嵌入式粒子过滤器进行视觉跟踪

利用多特征混沌粒子滤波的视觉目标跟踪方法

视觉跟踪中的粒子滤波算法研究进展 (2011年)

Linux下基于粒子滤波目标跟踪代码

C语言编写的粒子滤波跟踪程序

粒子滤波跟踪程序源代码

MATLAB 粒子滤波目标跟踪代码

粒子滤波目标跟踪MATLAB

最新资源

粒子滤波用于视觉跟踪

粒子滤波视频跟踪