
Applications of optimization
with Xpress-MP
Revised translation from the French language edition of:
Programmation linéaire
by Christelle Guéret, Christian Prins, Marc Sevaux
c
2000 Editions Eyrolles, Paris, France.
Translated and revised by Susanne Heipcke
Published by Dash Optimization Ltd.
www.dashoptimization.com

Published by:
Dash Optimization Ltd.
Blisworth House
Blisworth
Northants
NN7 3BX
United Kingdom
c
2000 Editions Eyrolles, Paris, France
Revised translation first published 2002
Translation and editing of this book has been supported by the EC Framework 5 project LISCOS
(contract G1RD-1999-00034).
Cover design: James Atkins Design, www.jades.co.uk
Manufacturing coordinator: Software Logistics, www.softwarelogistics.com
ISBN: 0-9543503-0-8
Last update 21 February, 2005

About the authors
Christelle Guéret is an Associate Professor in the Automatic Control and Production Systems department
at the ‘Ecole des Mines de Nantes’ (France). She received her Ph.D. degree in 1997 at the ‘Université
de Technologie de Compiègne’ and defended her Habilitation in December 2004 at the University of
Nantes in the IRCCyN laboratory. Her teaching courses include graph algorithms, scheduling and linear
programming. Her main research areas concern optimization problems in production and logistics, and
more specifically scheduling and vehicle routing problems.
Susanne Heipcke worked for BASF-AG (Germany) before joining Dash Optimization in 1998. Her Ph.D.
research (awarded in 1999 by the University of Buckingham) focused on the solution of large-scale in-
dustrial problems by a combination of constraint programming and mixed integer programming. More
recently she has worked on various aspects of modeling, including the development of teaching material
for Mosel, and interfaces to different types of solvers and solution methods. Since 2001 she has partic-
ipated in teaching the course on mathematical modeling in the OR master program at the University
Aix-Marseille II.
Christian Prins received his Ph.D. and Habilitation in computer science from Pierre and Marie Curie Uni-
versity (Paris VI). He is now a Professor in the Industrial Systems Engineering Department at the University
of Technology of Troyes (UTT, France). His research interest include combinatorial optimization, vehicle
routing and transportation, scheduling and algorithmic tools for optimization (e.g. metaheuristics and
reusable software components). He is a member of the editorial board of Computers and Operations
Research.
Marc Sevaux is an Associate Professor at the University of Valenciennes (France). He received his Ph.D.
degree in 1998 at the Pierre and Marie Curie University (Paris VI) and defended his Habilitation in July
2004 at the University of Valenciennes in the LAMIH laboratory. He is primarily interested in solving com-
binatorial optimization problems, particularly planning, scheduling and routing problems. Marc Sevaux is
the coordinator of the EUropean chapter on MEtaheuristics (EU/ME). He is an associate editor of Journal
of Heuristics and INFOR.

Contents
Foreword 1
Preliminaries 4
What you need to know before reading this book . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Symbols and conventions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
I Developing Linear and Integer Programming models 6
1 What is modeling? Why use models? 7
1.1 The chess set problem: description . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.1.1 A first formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.2 Linear Programming . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.3 Solving the chess set problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.3.1 Building the model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.3.2 The results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.3.3 Divisibility again . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
1.3.4 Unboundedness and infeasibility . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.4 Diagnosing infeasibility and unboundedness . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.5 The benefits of modeling and optimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.6 Data in models . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
1.7 References and further material . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2 Typical LP model constructs 19
2.1 Simple upper and lower bounds . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2.2 Flow constraints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
2.3 Simple resource constraints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.4 Material balance constraints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.5 Quality requirements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
2.6 Accounting constraints, non-constraining ‘constraints’ . . . . . . . . . . . . . . . . . . . . . . 25
2.7 Blending constraints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.8 Modes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2.9 Soft constraints and ‘panic variables’ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
2.10 Objective functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.10.1 Minimax objective functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.10.2 Ratio objective functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
3 Integer Programming models 30
3.1 IP modeling objects: ‘global entities’ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
3.2 IP solving: the ideas behind Branch and Bound . . . . . . . . . . . . . . . . . . . . . . . . . . 31
3.3 Modeling with binary variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.3.1 Do/don’t do decisions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.3.2 Logical conditions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
3.3.2.1 Choice among several possibilities . . . . . . . . . . . . . . . . . . . . . . . . . 34
3.3.2.2 Simple implications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
3.3.2.3 Implications with three variables . . . . . . . . . . . . . . . . . . . . . . . . . 35
3.3.2.4 Generalized implications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
3.3.3 Products of binary variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
3.3.4 Dichotomies: either/or constraints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
3.4 Binary variables ‘do everything’ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
3.4.1 General integers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.4.2 Partial integers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.4.3 Semi-continuous variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
i Applications of optimization with Xpress-MP
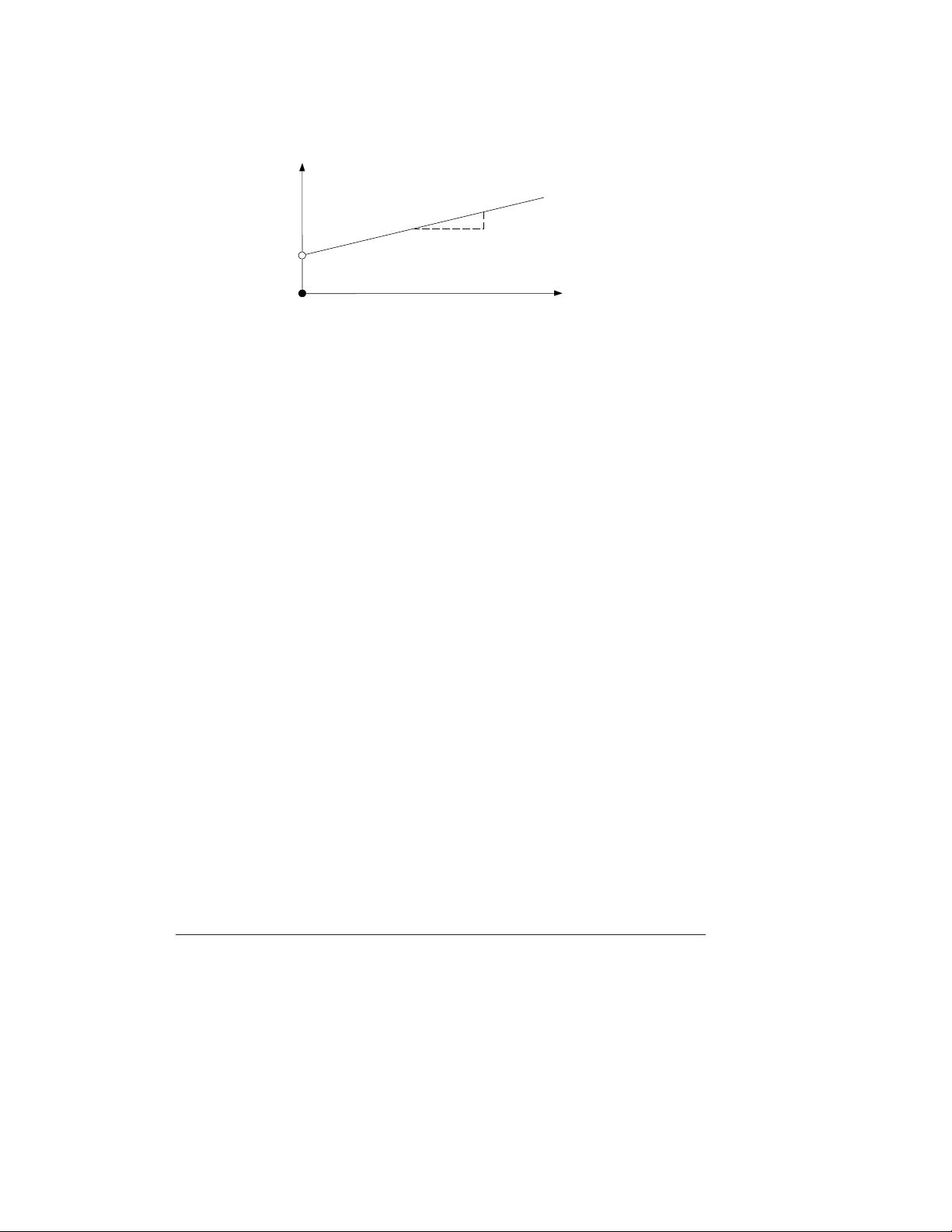
3.4.4 Special Ordered Sets of type 1 (SOS1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.4.5 Special Ordered Sets of type 2 (SOS2) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
3.5 Connecting real variables to binary variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
3.5.1 Modeling fixed costs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
3.5.2 Counting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
3.5.3 Partial integers again . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.5.4 Price breaks and economies of scale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.5.5 The product of a binary and a real variable . . . . . . . . . . . . . . . . . . . . . . . . 44
3.6 References and further material . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
4 Quadratic Programming 46
4.1 Revenue optimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
4.2 Portfolio optimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
4.3 References and further material . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
II Application examples 48
Classification of the example problems 49
5 The basics of Xpress-MP 55
5.1 Introductory example . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
5.1.1 Using Xpress-Mosel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
5.1.2 Using Xpress-IVE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
5.2 Modeling with Mosel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
5.2.1 The burglar problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
5.2.2 Reading data from text files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
5.2.3 Reserved words . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
6 Mining and process industries 62
6.1 Production of alloys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
6.1.1 Model formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
6.1.2 Implementation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
6.1.3 Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
6.2 Animal food production . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
6.2.1 Model formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
6.2.2 Implementation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
6.2.3 Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
6.3 Refinery . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
6.3.1 Model formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
6.3.2 Implementation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
6.3.3 Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
6.4 Cane sugar production . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
6.4.1 Model formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
6.4.2 Implementation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
6.4.3 Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
6.5 Opencast mining . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
6.5.1 Model formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
6.5.2 Implementation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
6.5.3 Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
6.6 Production of electricity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
6.6.1 Model formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
6.6.2 Implementation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
6.6.3 Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
6.7 References and further material . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
7 Scheduling problems 81
7.1 Construction of a stadium . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
7.1.1 Model formulation for question 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
7.1.2 Implementation of question 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
7.1.3 Results for question 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
7.1.4 Model formulation for question 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
7.1.5 Implementation of question 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
7.1.6 Results for question 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
7.2 Flow-shop scheduling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
Contents ii Applications of optimization with Xpress-MP











































