环形链表介绍以及题目解析-力扣141、142

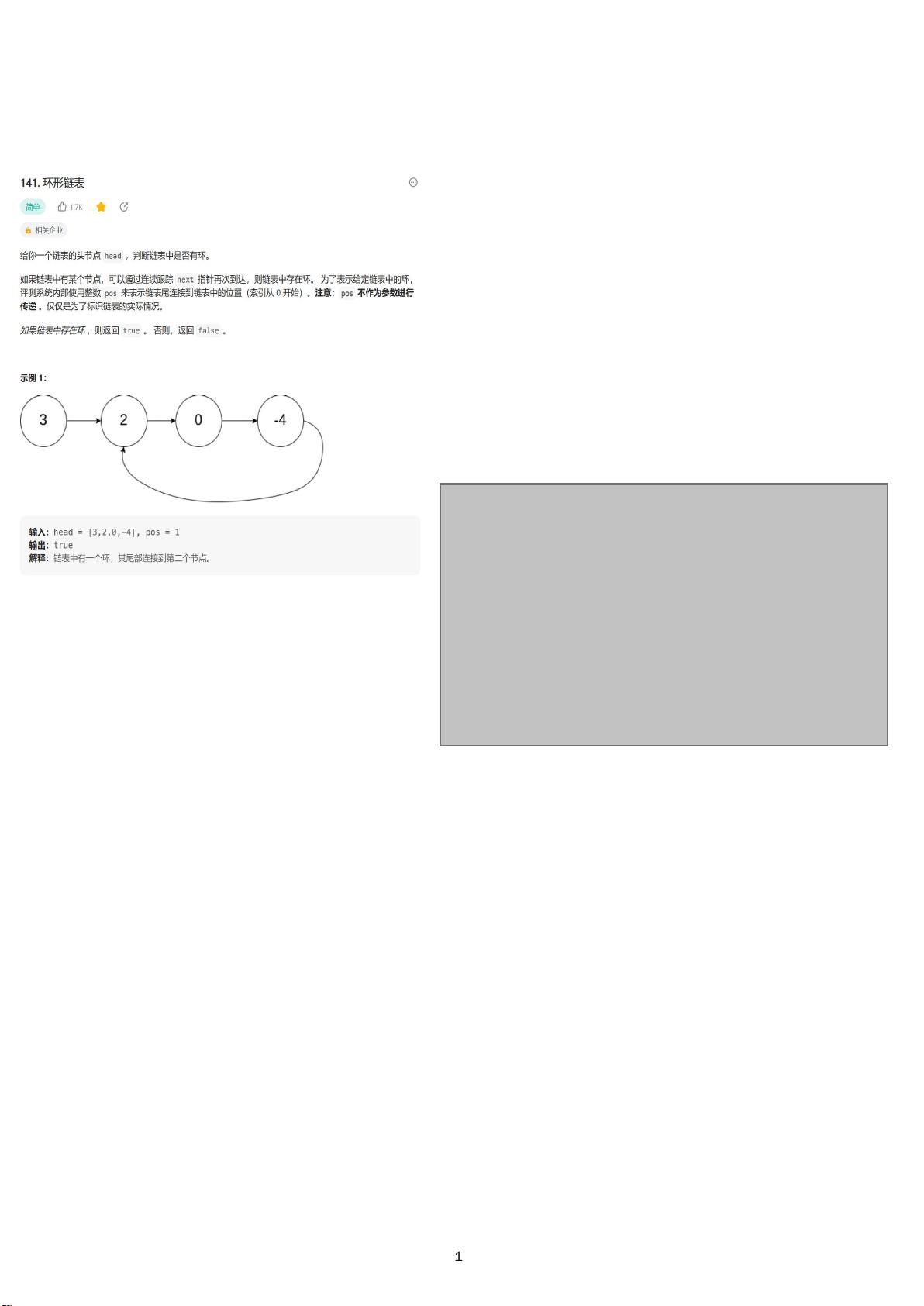
环形链表是一种特殊的数据结构，它与普通链表的区别在于存在一个或多个节点的引用形成了一个闭合的环。这种结构在某些算法问题中有着广泛的应用，例如力扣（LeetCode）上的题目141和142就涉及到环形链表的判断和处理。 在环形链表中，判断是否存在环的常用方法是使用快慢指针。快慢指针的概念是设置两个指针，一个称为快指针（fast），每次移动两步；另一个称为慢指针（slow），每次移动一步。如果链表存在环，那么快指针最终会在环内追上慢指针，因为快指针的速度是慢指针的两倍。如果链表没有环，快指针会先到达NULL，此时可以确定链表无环。 以下是判断环形链表的代码实现： ```c bool hasCycle(struct ListNode *head) { struct ListNode *fast = head, *slow = head; while (fast && fast->next) { fast = fast->next->next; slow = slow->next; if (fast == slow) { return true; } } return false; } ``` 在这个过程中，有几个关键点需要注意： 1. 快慢指针在环内相遇并不意味着它们一定在入环节点相遇，而是相遇点在环内。 2. 快慢指针的速度比（步伐差）不一定是2，只要保持一个固定的倍数关系，仍然能正确判断环的存在。 3. 若快指针每次走更多步，比如3步，只要保证快慢指针速度差为环的长度的因子，也可以正确判断。例如，若快指针每次走3步，慢指针每次走1步，那么当快指针在环内时，每过一圈，快慢指针之间的距离就会减小2步，最终依然会在某个点相遇。 找到环的存在后，我们可以找到入环节点。这可以通过将一个指针保留在相遇点，另一个指针重新从链表头开始，直到两者再次相遇，相遇的点即为入环节点。以下是实现代码： ```c struct ListNode *detectCycle(struct ListNode *head) { struct ListNode *fast = head, *slow = head; while (fast && fast->next) { fast = fast->next->next; slow = slow->next; if (fast == slow) { struct ListNode *meetNode = fast; while (meetNode != head) { meetNode = meetNode->next; head = head->next; } return meetNode; } } return NULL; } ``` 在这个代码中，`detectCycle`函数在找到相遇点后，通过两个指针分别以一步一跳的方式前进，直到相遇点与头节点重合，这时的相遇点就是入环节点。 总结来说，环形链表的关键在于理解其结构特性，并掌握快慢指针法判断环的存在以及寻找入环节点的方法。在实际编程中，这些技巧常用于解决复杂的问题，如检测循环依赖、遍历有环图等。熟悉这些概念和方法对于解决类似力扣上的题目至关重要。