牛顿迭代法收敛定理 (2).docx

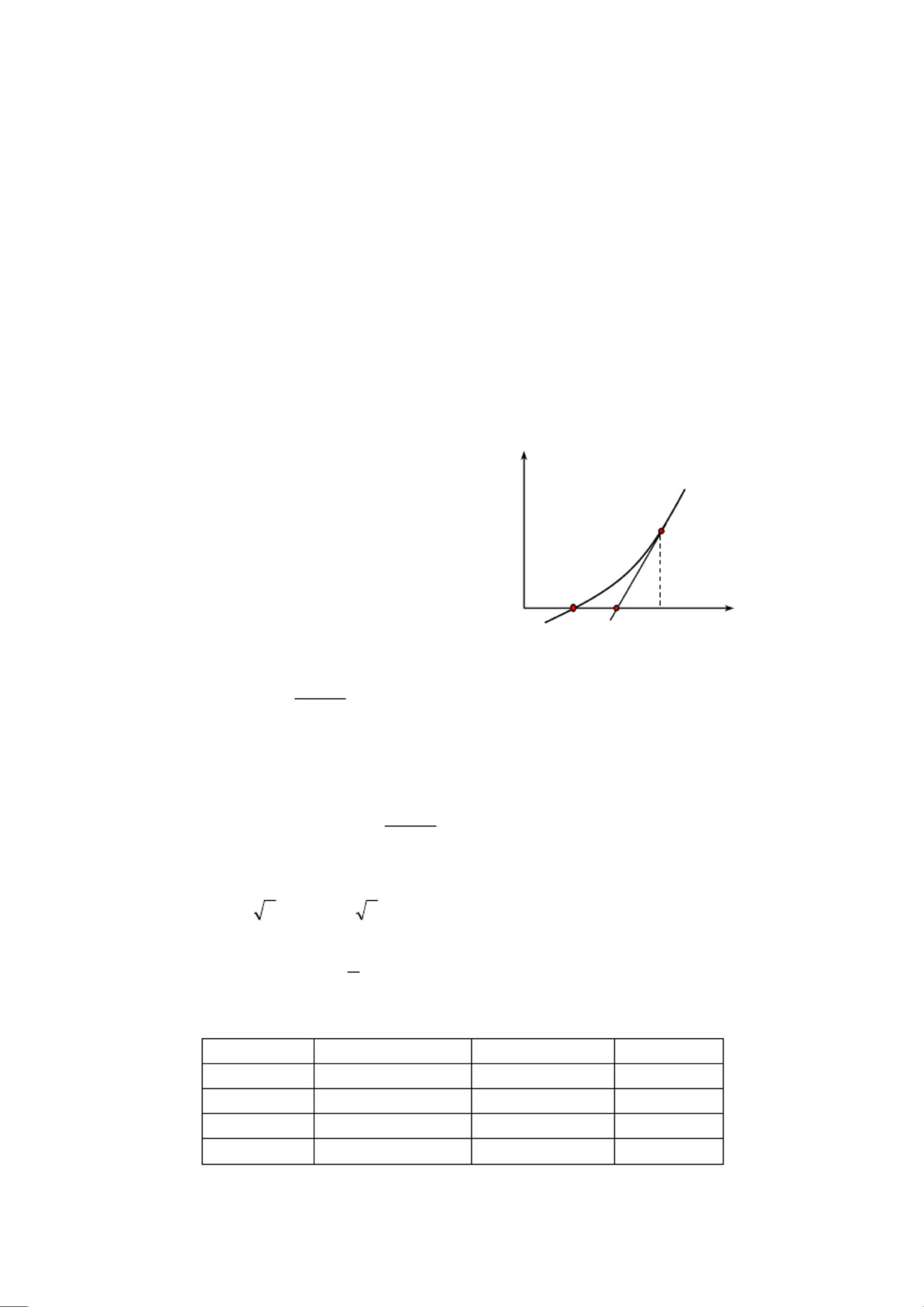
牛顿迭代法是一种在数值分析中寻找非线性方程数值解的常用方法，由数学家艾萨克·牛顿提出。它基于微积分的基本原理，即局部线性化思想，将复杂的非线性问题转化为简单的线性问题来解决。这种方法在科学计算中有着广泛的应用，包括但不限于物理学、工程学、经济学等领域。 牛顿迭代法的核心在于泰勒级数的前两项展开，即在函数f(x)在某点x0处的切线近似。具体步骤如下： 1. 选择一个初始猜测值x0，它接近于方程f(x) = 0的解。 2. 计算函数在x0处的导数f'(x0)。 3. 构造切线方程：f(x) ≈ f(x0) + (x - x0)f'(x0)，解这个线性方程得到新的近似值x1 = x0 - f(x0)/f'(x0)。 4. 重复上述过程，用x1替换x0，得到更精确的近似解x2，如此迭代下去，直至满足一定的精度要求。 牛顿迭代法的一大优势是其快速的收敛性。对于二阶可导的函数，牛顿法通常呈现出二阶收敛，这意味着每次迭代，解的误差大约会减少原来的平方。例如，求平方根的算法展示了这一特性，初始值为1.4时，经过三次迭代，解的精度就达到了小数点后15位。 然而，牛顿迭代法的收敛性是有条件的，它依赖于函数在解附近的二阶连续导数，并要求初始值足够接近真实解。如果初始值选取不当，可能会导致迭代序列发散或者收敛到错误的解。例如，对于方程f(x) = x^3 - x - 3，当初始值选取为0时，迭代序列会在x = 0附近陷入循环，无法找到正确的实根。 因此，在实际应用牛顿迭代法时，需要注意以下几点： - 初始值的选择至关重要，需要尽可能靠近实际解。 - 必须确保函数在迭代区间内有良好的导数行为，避免出现导数为0的情况，这可能导致迭代失败。 - 对于可能存在的多个解，初始值的选取可能影响最终找到哪个解。 - 当牛顿法不收敛时，可以考虑使用其他数值方法，如二分法或拟牛顿法等。 牛顿迭代法是一种强大的数值解法，但在使用时需谨慎选择初始值，并结合具体问题的特点进行调整，以确保其收敛性和准确性。在数据库和计算机科学领域，这类方法常用于优化问题、求解复杂系统的平衡点以及各种数值计算任务。