第一章：定量分析的误差及结果的数据处理2022优秀文档.ppt

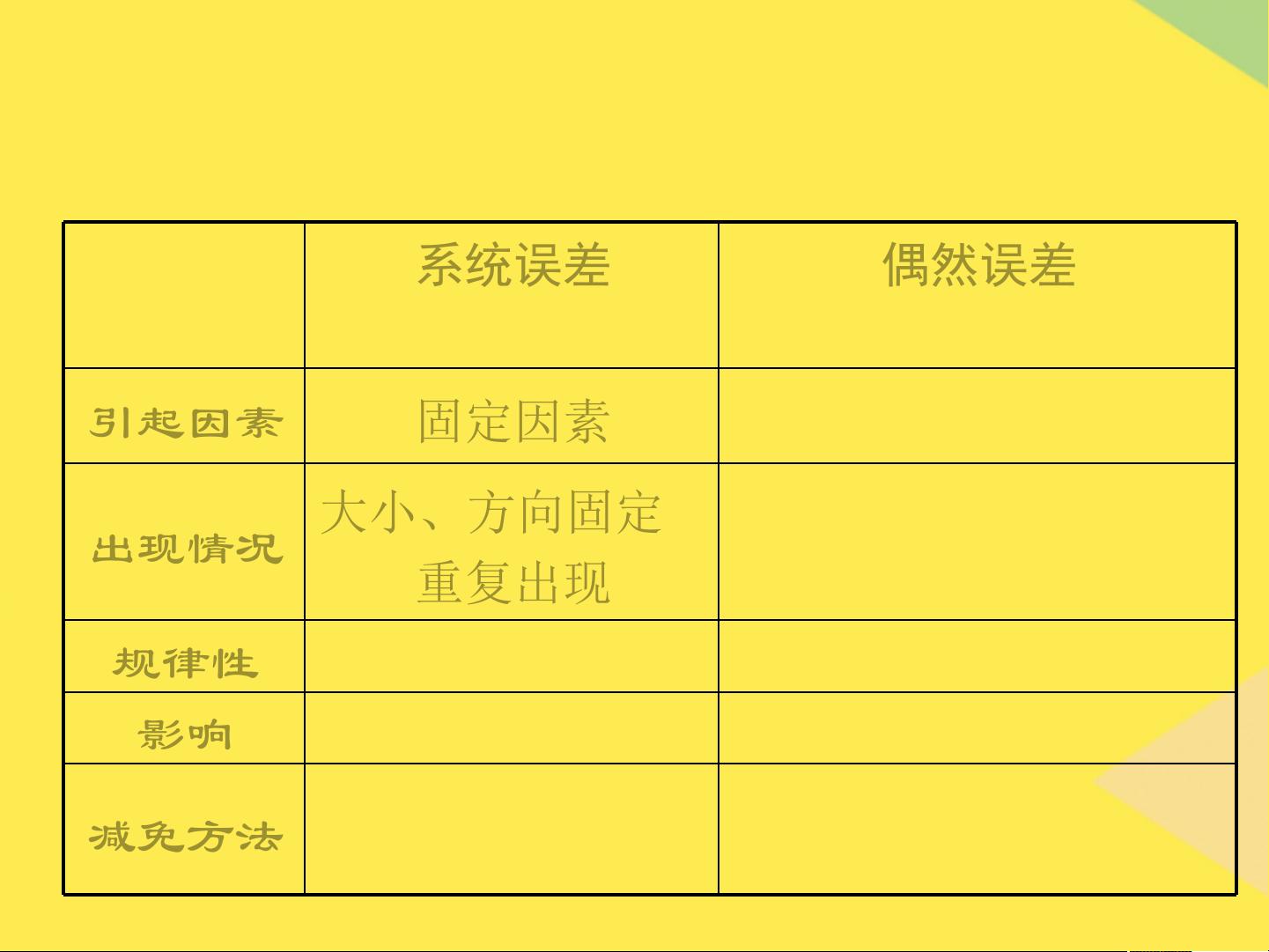
在定量分析中，误差分析是极其关键的一环，因为它直接影响到实验结果的可靠性和准确性。本章主要讨论了定量分析中的误差类型、表示方法以及如何处理这些误差。 我们了解了化学计量的各种表达方式，如物质的量浓度、质量摩尔浓度、摩尔分数、物质的质量分数和质量浓度。这些都是用来描述溶液中各组分含量的量度，它们各有不同的应用场景和计算方法。 误差的分类主要包括系统误差、偶然误差和过失误差。系统误差是由固定的、可预测的原因引起的，如方法误差、仪器和试剂误差以及主观误差。这些误差具有重复性，可以通过校正方法来减轻。而偶然误差则是由随机因素造成的，遵循统计规律，可通过增加平行测定次数来减少其影响。过失误差是明显的错误，通常需要重新进行实验。 在处理误差时，分析工作者需要查明误差产生的原因，并采取适当的控制措施。例如，通过仪器校正可以消除仪器或器皿的刻度误差；方法对照、空白对照和阳性对照实验则有助于检验和消除方法误差。对于随机误差，增加平行测定次数是一种有效的减小误差的方法。 误差的表示方法包括准确度和误差。准确度是测量结果与真实值的接近程度，通常通过相对误差来衡量。绝对误差是测量值与真值的差值，而相对误差是绝对误差在真值中的比例。偏差和精密度也是评估结果质量的重要指标，偏差是指各次测定值与平均值的差异，而精密度则是反映重复测量结果的一致性。 在实际操作中，如需保证称量的相对误差不超过0.1%，则需要根据万分之一分析天平的绝对误差（±0.0002g）计算最小称量质量。同样，如果要求相对误差不大于2%，也需要进行相应的计算以确定合适的称量质量。选择合适的样品量和测量仪器对于达到预期的准确度和精密度至关重要。 定量分析的误差处理和数据处理是一项精细的工作，需要理解误差的来源，运用适当的统计方法和实验技巧来提高分析结果的可靠性。通过深入学习和实践，分析工作者可以更好地理解和控制误差，从而提高实验的科学性和有效性。