计算机组成原理-第9周 周六 除法运算.pptx
计算机组成原理中的除法运算是一项复杂且重要的计算任务,它涉及到计算机硬件层面的数据表示和运算。在本课程中,我们将探讨几种不同的数据类型及其运算,包括无符号和有符号数的机器数编码,定点数与浮点数的运算规则。 定点数是表示数值时,小数点位置固定不变的一种方式,它可以进行加、减、移位和乘法运算。定点除法通常涉及将被除数减去除数,并根据结果判断商的位数。例如,在笔算除法中,通过恢复余数法进行除法运算,即不断用被除数减去除数,当被除数大于或等于除数时,商上加1,然后左移一位,继续这个过程,直到所有位都被处理。在机器实现中,这一过程更为复杂,需要考虑进位、溢出和符号位的处理。 浮点数则是用于表示大范围数值的格式,它包括一个指数和一个尾数。浮点加减乘除运算涉及到对指数和尾数分别进行运算,同时还需要处理规格化和下溢、上溢的情况。浮点除法通常先将两个数转换成相同指数,然后对尾数进行相除,最后调整指数得到最终结果。 在定点除法中,有一个关键的步骤是确定商的符号。商的符号是被除数和除数符号位的异或结果,这在笔算除法和机器除法中都是一致的。例如,如果两者符号位相同,则商为正,反之为负。而在机器除法中,商的计算位置可能不固定,余数需要根据上一次的商位进行左移,并可能需要加上或减去除数的倍数来恢复余数。 恢复余数法是一种直观的算法,类似于手动除法,但需要注意的是,当最后一步的商为0时,需要恢复余数,以确保正确性。例如,在一个具体的例子中,通过不断迭代和判断余数的正负,可以得出正确的商和余数。 逻辑左移在计算机中是一种常见的操作,它将所有的位向左移动指定的次数,相当于乘以2的幂次。在除法运算中,逻辑左移可以帮助我们处理位移操作,特别是当余数需要左移时,它能够简化计算过程。 定点和浮点数的除法运算在计算机组成原理中是核心内容,理解并掌握这些概念对于理解和设计计算机硬件至关重要。这些运算不仅涉及到数值的逻辑处理,还牵涉到硬件设计中的ALU(算术逻辑单元)如何执行这些复杂的操作。因此,深入理解这些运算的原理对于计算机科学家和工程师来说是必不可少的。
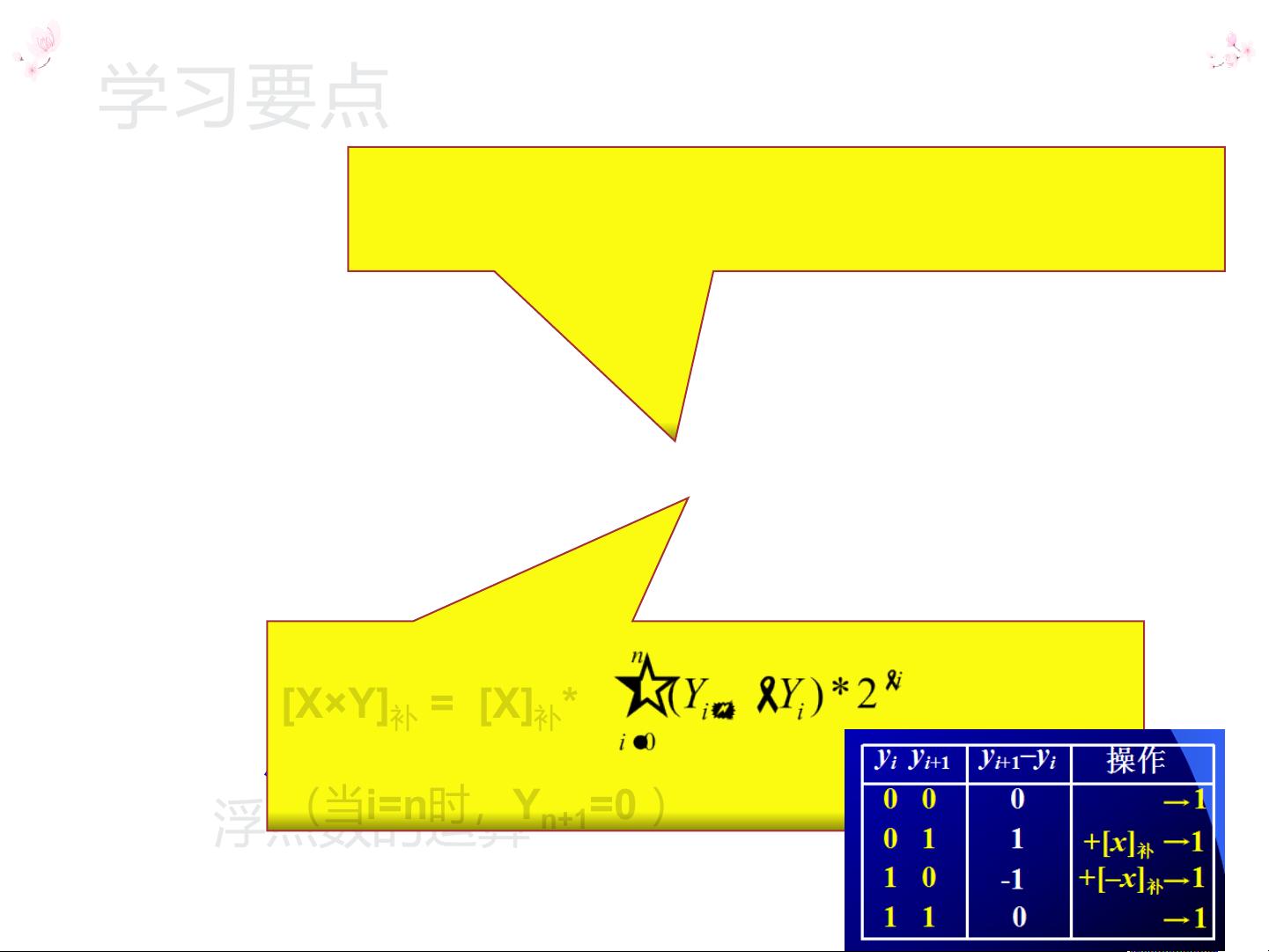

剩余14页未读,继续阅读

- 粉丝: 76
- 资源: 14
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功