成都理工大学离散数学课程资料复习资料

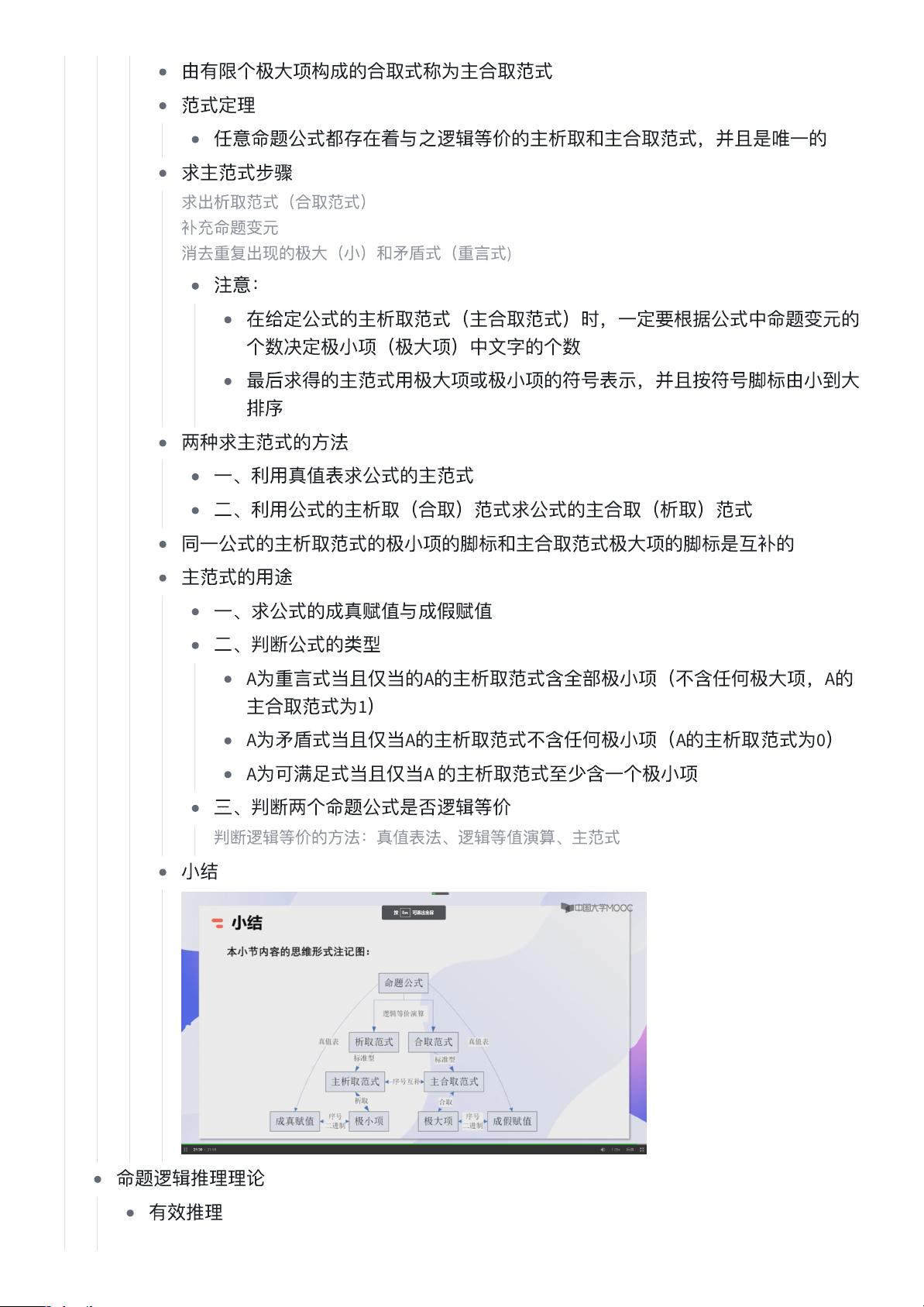
（+q1321087802免费拿电子版思维导图）包含内容：1. 课程内容 集合与逻辑 集合的基本概念与运算 逻辑命题与逻辑运算 谓词逻辑 关系与函数 关系的定义与性质 等价关系与偏序关系 函数及其性质 图论 组合数学 计数原理：加法原理与乘法原理 排列与组合 二项式定理 代数结构 代数系统的基本概念 群、环与域 格与布尔代数 递归与生成函数 递归关系的求解 生成函数的基本概念与应用 教材与参考书目 《离散数学及其应用》（Kenneth H. Rosen） 《离散数学》（Liu C. L.） 《离散数学与其应用》（吴伟光 译） 3. 重要知识点 集合与逻辑 掌握集合的运算及其性质 理解命题逻辑与谓词逻辑的基本概念 关系与函数 掌握等价关系与偏序关系的判定 理解函数的单射、满射与双射 图论 熟悉各种图的表示方法 掌握图的遍历算法 组合数学 掌握排列与组合的计算方法 理解二项式定理及其应用 ### 成都理工大学离散数学课程复习资料精要 #### 一、课程内容概览 **1. 集合与逻辑** - **集合的基本概念与运算** - 集合的概念、元素与集合的关系、集合间的包含关系、并集、交集、差集、补集等基本运算。 - **逻辑命题与逻辑运算** - 命题的概念、真值、命题联结词（否定、合取、析取、蕴含、等价）及其真值表。 - **谓词逻辑** - 谓词的概念、量词（全称量词、存在量词）、谓词公式的构造及解释。 **2. 关系与函数** - **关系的定义与性质** - 关系的定义、关系矩阵、关系图、自反性、对称性、传递性等性质。 - **等价关系与偏序关系** - 等价关系的特点（自反性、对称性、传递性）、等价类、商集；偏序关系的特点（自反性、反对称性、传递性）。 - **函数及其性质** - 函数的概念、定义域、值域、函数的合成、单射、满射、双射等。 **3. 图论** - **图的定义与性质** - 图的概念、顶点、边、路径、回路、连通性、度数等基本概念。 - **图的遍历算法** - 深度优先搜索（DFS）、广度优先搜索（BFS）等算法。 **4. 组合数学** - **计数原理** - 加法原理、乘法原理。 - **排列与组合** - 排列的计算方法、组合的计算方法、组合恒等式。 - **二项式定理** - 二项式定理的表述、证明、应用。 **5. 代数结构** - **代数系统的基本概念** - 半群、幺半群、群、环、域、格、布尔代数等概念。 - **群、环与域** - 群的定义、群的性质；环的定义、环的分类；域的定义、特征。 - **格与布尔代数** - 格的概念、布尔代数的定义、布尔运算的性质。 **6. 递归与生成函数** - **递归关系的求解** - 线性递归方程、非线性递归方程、特征根法。 - **生成函数的基本概念与应用** - 平凡生成函数、指数生成函数、生成函数的应用。 #### 二、重要知识点详解 **1. 集合与逻辑** - **掌握集合的运算及其性质** - 熟练运用集合的并集、交集、差集、补集等运算，理解这些运算的基本性质。 - **理解命题逻辑与谓词逻辑的基本概念** - 命题逻辑中的命题联结词（否定、合取、析取、蕴含、等价）及其真值表，理解谓词逻辑中的谓词、量词的概念。 **2. 关系与函数** - **掌握等价关系与偏序关系的判定** - 等价关系的定义与判定，偏序关系的定义与判定。 - **理解函数的单射、满射与双射** - 单射、满射、双射的定义及其性质。 **3. 图论** - **熟悉各种图的表示方法** - 使用邻接矩阵、邻接表等方式表示图。 - **掌握图的遍历算法** - DFS、BFS算法的具体实现过程及其应用场景。 **4. 组合数学** - **掌握排列与组合的计算方法** - 掌握排列与组合的计算公式及其应用。 - **理解二项式定理及其应用** - 二项式定理的展开式、杨辉三角形等。 **5. 代数结构** - **代数系统的基本概念** - 了解不同代数系统的定义及其性质，如群、环、域等。 - **群、环与域** - 理解群、环、域的定义及性质，能够区分它们之间的区别。 **6. 递归与生成函数** - **递归关系的求解** - 掌握递归方程的解法，包括特征根法等。 - **生成函数的基本概念与应用** - 生成函数的概念及其在计数问题中的应用。 #### 三、数理逻辑之命题逻辑 - **命题逻辑的三次数学危机** - 毕达哥拉斯悖论：关于无理数的存在性问题，引发了数学上的第一次危机。 - 贝克莱悖论：涉及无穷小量的问题，导致了第二次数学危机。 - 罗素悖论：涉及到集合论中的悖论，引发了第三次数学危机。 - **命题的符号化** - 如何将自然语言中的命题转化为符号表示，包括使用逻辑联结词（合取、析取、蕴含、等价等）进行表达。 - **命题公式与范式** - 了解命题公式的定义，学习如何通过一系列等价变换将命题公式转化为范式，如析取范式（DNF）和合取范式（CNF）。 - **主范式及其求法** - 学习如何求一个命题公式的主析取范式（PDNF）和主合取范式（PCNF），包括求极小项和极大项的方法。 - **命题逻辑推理理论** - 理解有效推理的定义，掌握判断一个推理是否有效的几种方法：真值表法、逻辑等价演算法、主析取（合取）范式法以及命题演算推证的证明法。 #### 四、数理逻辑之谓词逻辑 - **谓词逻辑的基本概念** - 介绍谓词逻辑的基本概念，包括个体、个体常元、个体变元、谓词、谓词公式等。 - **谓词逻辑的特点** - 与命题逻辑相比，谓词逻辑能够更深入地分析命题内部结构，适用于更广泛的逻辑推理场景。 - **量词的使用** - 全称量词和存在量词的定义及其在谓词公式中的应用。 以上内容涵盖了成都理工大学离散数学课程的主要知识点，通过对这些知识点的学习和掌握，可以帮助学生更好地理解和应用离散数学的相关理论和技术。