高等数学课件-第三章第四节:单调性凹凸性.ppt
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
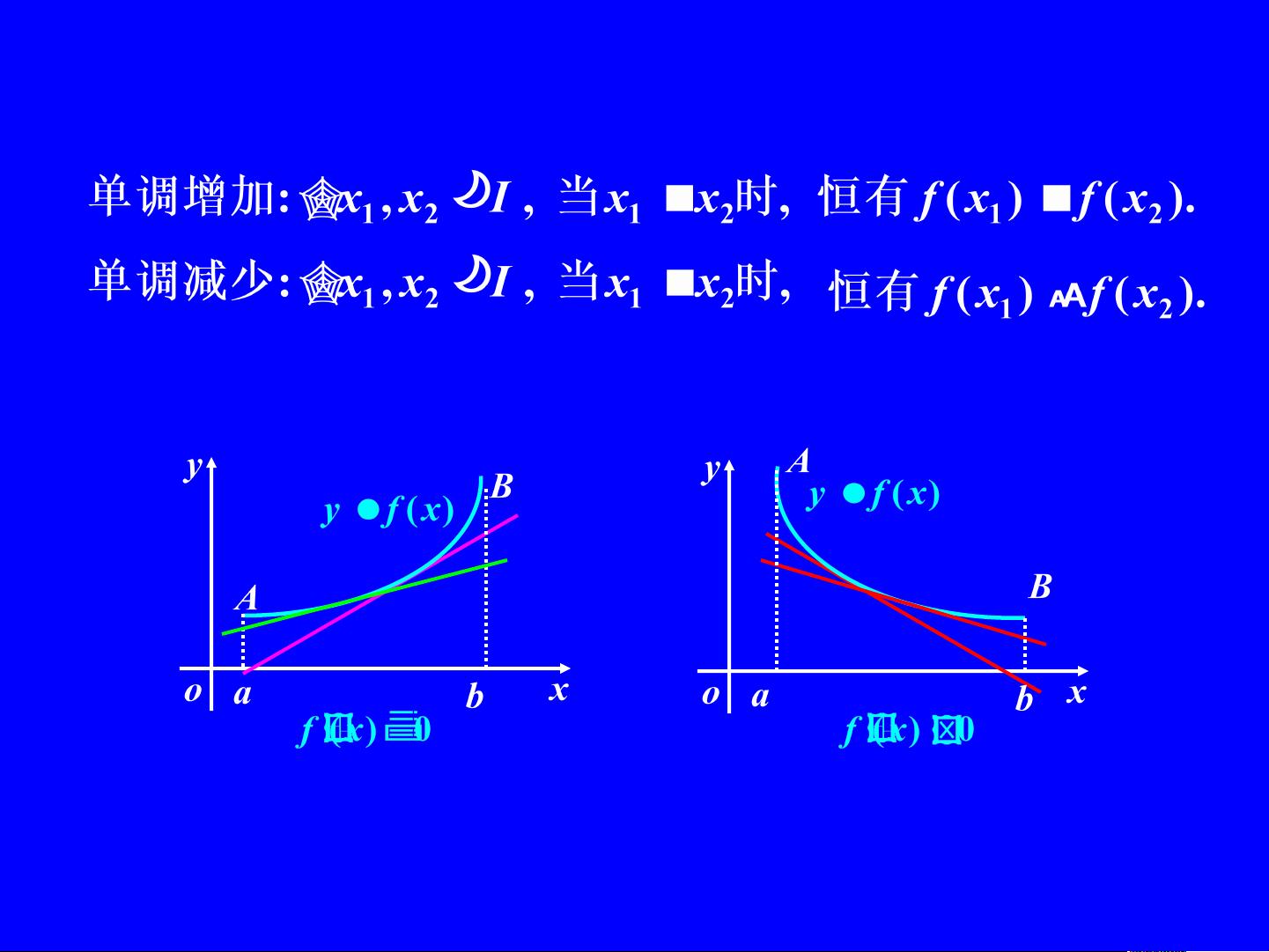
【高等数学】中的【函数的单调性】与【曲线的凹凸性】是微积分中的基本概念,对于理解和分析函数的性质至关重要。 一、单调性的判别法 1. 判断函数单调性的基本方法是利用导数。如果函数在某区间内导数非负,则函数在该区间内单调递增;若导数非正,则函数单调递减。例如,如果函数 \( f(x) \) 在区间 \( [a, b] \) 上导数 \( f'(x) \geq 0 \),那么 \( f(x) \) 在该区间内单调递增。反之,如果 \( f'(x) \leq 0 \),则函数单调递减。 2. 重要的是要注意,函数的单调性是对区间而言的,而非单个点。因此,我们不能仅凭一个点处的导数值来判断整个区间的单调性。例如,即使在某点 \( c \) 处导数为0,也不能立即断定函数在 \( c \) 左右两侧的单调性。 3. 导数等于零的点和不可导点可能是单调区间的分界点。求函数的单调区间通常需要找到这些点,并检查相邻区间的导数符号变化。 二、曲线的凹凸性与拐点 1. 凹凸性的定义是通过比较曲线上的弧段与通过该弧段两端点的切线之间的位置关系。如果曲线弧总位于切线的上方,我们称曲线在该区间内是凹的;反之,如果曲线弧总位于切线的下方,则称曲线在该区间内是凸的。 2. 判定曲线凹凸性的关键在于二阶导数。如果 \( f''(x) > 0 \),则 \( f(x) \) 在该区间内是凹的;若 \( f''(x) < 0 \),则曲线是凸的。当 \( f''(x) \) 为零或不存在时,可能意味着存在拐点。 3. 拐点是曲线从凹变凸或从凸变凹的点。在拐点处,曲线的切线会穿过曲线。求拐点通常需要找到二阶导数为0或者不存在的点,并验证这些点是否改变了一阶导数的符号,从而确定其是否为真正的拐点。 三、应用 1. 单调性和凹凸性在解决不等式和方程的根的问题中非常有用。如果可以证明函数在特定区间内单调,那么可以据此限制方程的根的数量,或证明某些不等式成立。 2. 拐点的求解有助于理解函数图像的变化情况,对图形的描绘和解析有着重要意义。 总结,高等数学中的单调性和凹凸性是分析函数性质的基础工具。通过导数和二阶导数,我们可以判断函数的增减趋势以及曲线的凹凸特性,这对于解决各种数学问题,尤其是几何和物理问题,具有极大的帮助。同时,理解和掌握这些概念也是进一步学习微积分和泛函分析的基石。




剩余28页未读,继续阅读

- 粉丝: 9673
- 资源: 4073
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功