信号与系统上机实验五连续系统的频域分析及连续信号的采样与重构借鉴.pdf

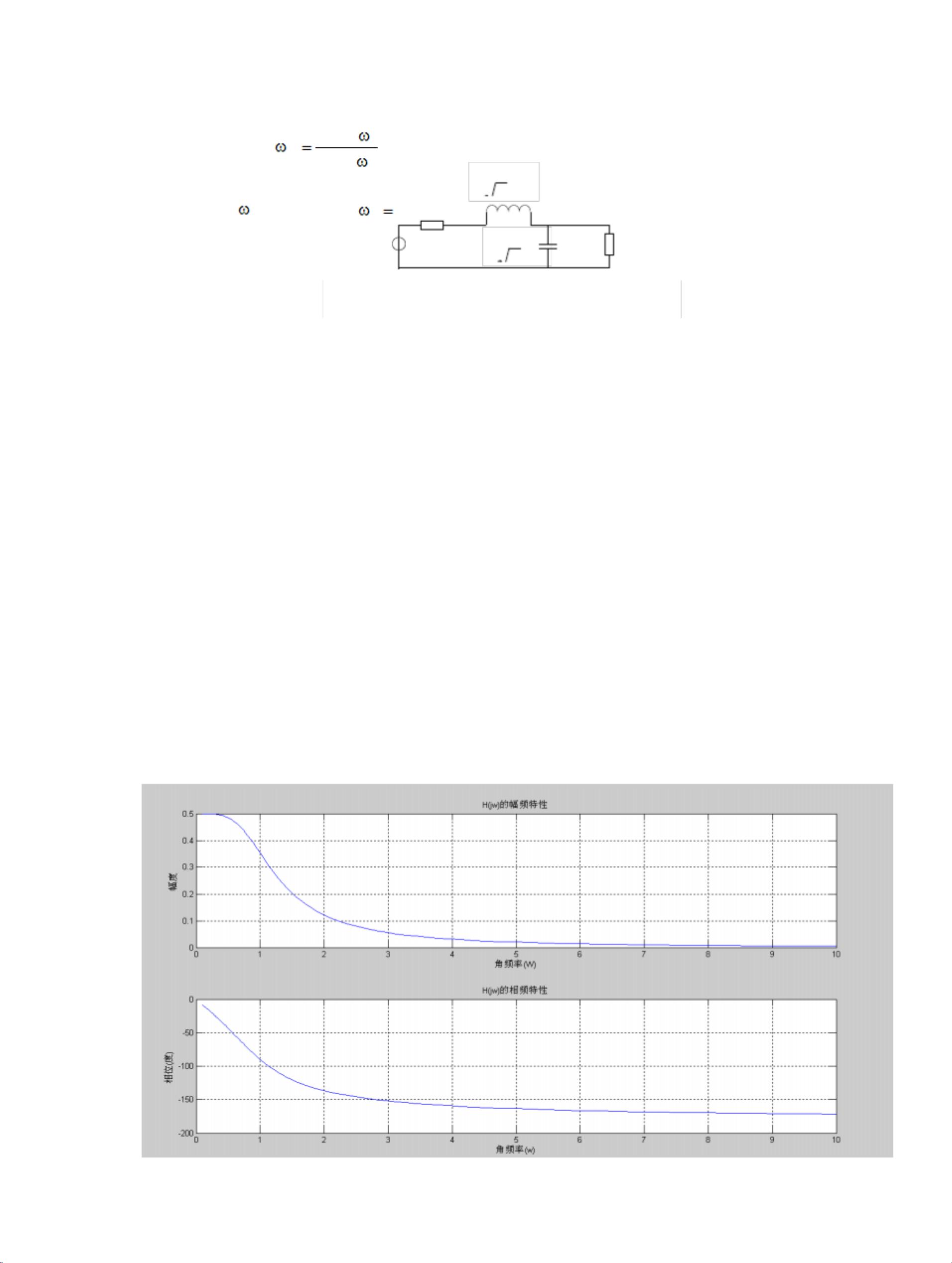
《信号与系统》上机实验五主要探讨了连续系统的频域分析以及连续信号的采样与重构。实验中，学生需要使用MATLAB软件对一个最平坦幅度型二阶低通滤波器进行模拟，以此来理解和掌握信号处理的基本概念。 实验中提到的最平坦幅度型二阶低通滤波器是一种常见的信号处理电路，它的主要功能是让低于某一特定频率（即截止频率）的信号通过，而高于该频率的信号则被衰减。在MATLAB程序中，利用`freqs`函数计算了滤波器的幅度响应`h1`和相位响应`h2`。通过绘制这两个响应的图形，可以直观地对比实际结果与理论分析的差异。例如，`h1`表示的是滤波器对不同角频率信号的衰减程度，而`h2`则反映了信号相位的变化。这有助于理解滤波器的频率选择性。 接着，实验内容涉及到连续信号的采样与重构。采样是将连续时间信号转换为离散时间信号的过程，而重构则是根据采样值恢复原始连续信号。在本实验中，选取了一个指数衰减信号`exp(-1000*abs(t))`作为例子。采样频率`fs`与信号最高频率`fm`的关系决定了重构信号的质量，通常应满足奈奎斯特定理，即`fs >= 2fm`。实验中，分别考虑了三种不同的采样情况： 1. 当`fs = 5000m, mc = 1, ms = T/`时，计算并比较了重构信号与原始信号的误差。 2. 当`fs = 10000m, mc = 1.1, ms = T/`时，同样进行了信号重构和误差分析。 3. 当`fs = 2500m, mc = 9, ms = T/`时，再次进行上述步骤。 通过MATLAB程序，计算了采样信号、重构信号以及两者之间的误差。使用`stem`和`plot`函数绘制了采样信号的时域表示、重构信号以及误差随时间变化的图形。这些图形直观地揭示了采样频率对重构信号质量的影响：当采样频率过低时，重构信号可能会出现失真，误差较大；而提高采样频率可以有效减少重构误差，更好地恢复原始信号。 总结来说，这个实验不仅让学生掌握了频域分析的方法，还深化了他们对信号采样与重构理论的理解，尤其是奈奎斯特定理的实际应用。通过对不同采样条件的比较，实验强调了适当选择采样频率对于信号处理的重要性，这对于理解和应用数字信号处理技术具有重要意义。