线性代数是数学的一个重要分支,主要研究向量、矩阵和线性方程组的性质。本测试题涵盖了线性代数第四、五章的关键概念,包括秩、特征值、相似矩阵、正定矩阵、正交矩阵以及线性相关性等。 1. 矩阵的秩(Rank)反映了矩阵行向量或列向量的最大线性无关组的数目。如果一个3x3矩阵A的方程组基础解系包含两个解向量,那么秩(A) = 3 - 2 = 1。 2. 向量组的相关性和无关性是线性代数中的基本概念。若向量组可以被其他向量线性表示,则称其线性相关;若无法表示,则为线性无关。 3. 向量组的秩是向量组中最大线性无关向量的数量。对于一个向量组,其秩可能小于向量的数量。 4. 特征值是矩阵乘以其特征向量后得到的标量。如果A是一个n阶可逆矩阵,那么λ是A的特征值,那么1/λ是A^(-1)的特征值,|A|/λ是A的伴随矩阵A*的特征值。 5. 如果A有一个特征值为-2,那么其共轭转置A^H也有一个特征值为-2,因此A+A^H会有两个特征值为0(因为A^H的特征值是A的共轭),所以A+A^H必有一个特征值为4。 6. n阶方阵A与对角阵相似的条件是A有n个线性无关的特征向量。 7. 三阶方阵A的特征值为-2, 1, 1,如果B与A相似,那么B的特征值也是-2, 1, 1。 8. 一个矩阵为正定矩阵的条件是所有顺序主子式都大于0,即当a > 1时,矩阵是正定的。 9. 正交矩阵的定义是其转置等于其逆,即A^T = A^(-1),所以选项C满足这个条件。 10. 矩阵的行向量组线性无关意味着矩阵是满秩的,所以矩阵的列空间等于行空间,因此矩阵仅有零解的充分必要条件是列向量组线性无关,选D。 11. 命题B正确,因为向量组的秩最多等于向量的数量。 12. 非齐次线性方程组的齐次对应方程组有非零解,意味着非齐次方程组至少有非零解。因此,选项C正确。 13. 线性方程组的解的加法性质表明,如果α是Ax=b的解,β是Ax=0的解,那么α+β也是Ax=b的解,所以选项C正确。 14. 相似矩阵具有相同的特征多项式、特征值,但特征向量不一定相同,因此D不正确。 15. A是正定矩阵的充要条件是所有顺序主子式大于0,所以选项D正确。 16. 选项C不正确,因为若向量组A可由线性表示,表示式可能唯一也可能不唯一,取决于其他向量的关系。 解答题部分涉及向量组的线性相关性和线性无关性、矩阵的秩、非齐次线性方程组的通解、特征值和特征向量的应用、二次型的正定性以及正交变换等问题。具体解答需要对每个问题进行详细计算,这里仅提供了题目的概述。 通过这些自测题,学生可以检验自己对线性代数基本概念和方法的理解,以便更好地掌握这门学科。

- 粉丝: 2
- 资源: 4
 我的内容管理
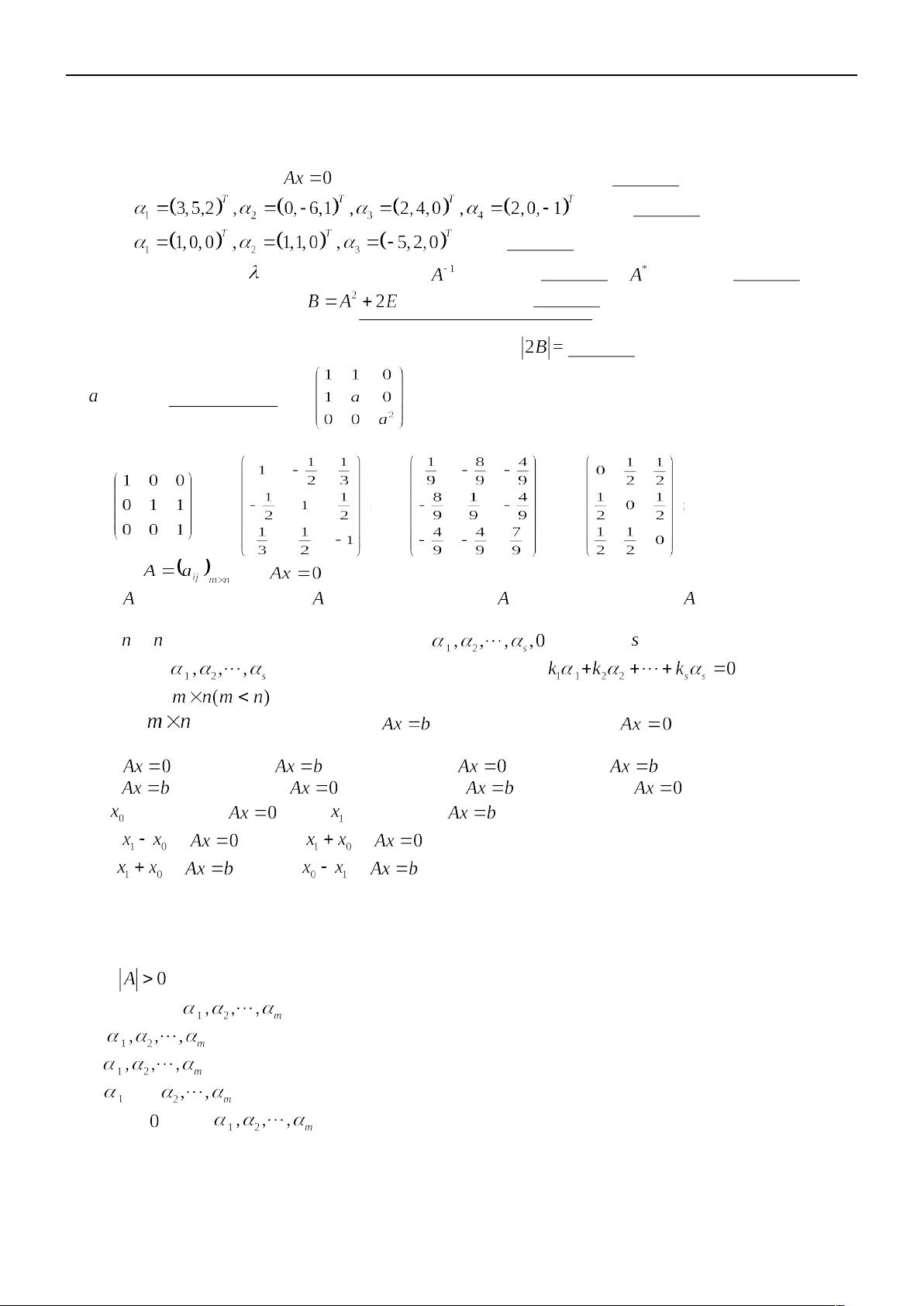
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功