SVM入门 很经典哦！！！

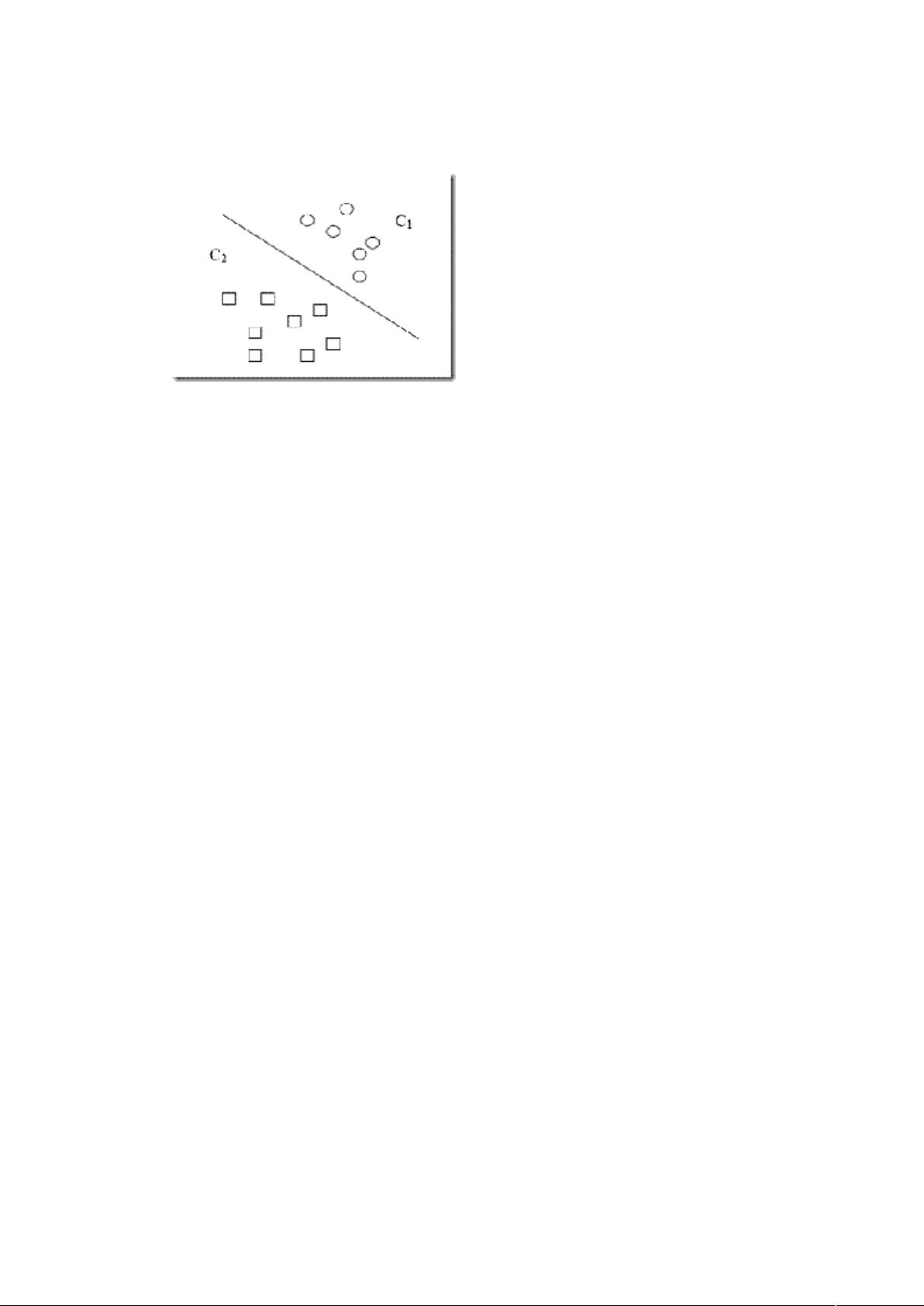
支持向量机（Support Vector Machine, SVM）是一种监督学习算法，由Cortes和Vapnik于1995年提出。SVM的核心思想在于通过最大化分类边距（margin）来构建决策边界，从而实现对数据的有效分类。这种算法特别适用于小样本、非线性以及高维空间中的模式识别任务，同时也可用于函数拟合等其他机器学习问题。 SVM的理论基础建立在统计学习理论的VC维理论和结构风险最小化原理上。VC维是衡量一个函数类复杂性的指标，数值越高，表示该函数类能够拟合的数据集种类越多，问题也就更复杂。SVM的一个关键特性是，即使在高维空间中，它也能有效地处理问题，这得益于其对样本维度的独立性，使得SVM在处理如文本分类这样的高维数据时表现出色。 结构风险最小化原则强调在模型的复杂性和学习能力之间找到平衡。在机器学习中，由于我们通常无法得知真实模型，因此需要通过模型在样本数据上的表现来估计模型的性能。经验风险是模型在已知样本上的误差，而置信风险则反映了模型在未知数据上的不确定性。统计学习理论引入泛化误差界的概念，将真实风险分解为经验风险和置信风险，以确保模型在新数据上的泛化能力。 SVM通过最小化结构风险，即经验风险与置信风险之和，来优化模型。这一过程通常涉及寻找最优超平面，即最大化样本到分类边界的间隔的超平面。在处理非线性问题时，SVM通过引入核函数，将原始数据映射到高维空间，使得原本在低维空间中难以划分的非线性数据变得可分。 除了上述特性，SVM还有以下显著优点： 1. 它能够处理非线性问题，通过核函数可以实现非线性决策边界。 2. SVM对过拟合有很好的抵抗能力，因为它关注的是样本间最大间隔的划分，而不是尽可能地拟合每个样本点。 3. 在高维空间中依然保持高效，这得益于其对样本维数的独立性。 4. SVM的优化目标是全局最优，因为它使用凸二次规划来求解问题，避免了局部最优解的困扰。 尽管SVM有诸多优点，但也存在一些挑战和限制，例如选择合适的核函数、处理大规模数据集时的计算复杂度以及对参数敏感等问题。然而，这些挑战并没有削弱SVM在众多领域，如文本分类、生物信息学、图像识别等的应用价值，它依然是机器学习领域的重要工具之一。