电子科技大学09应用随机过程试题

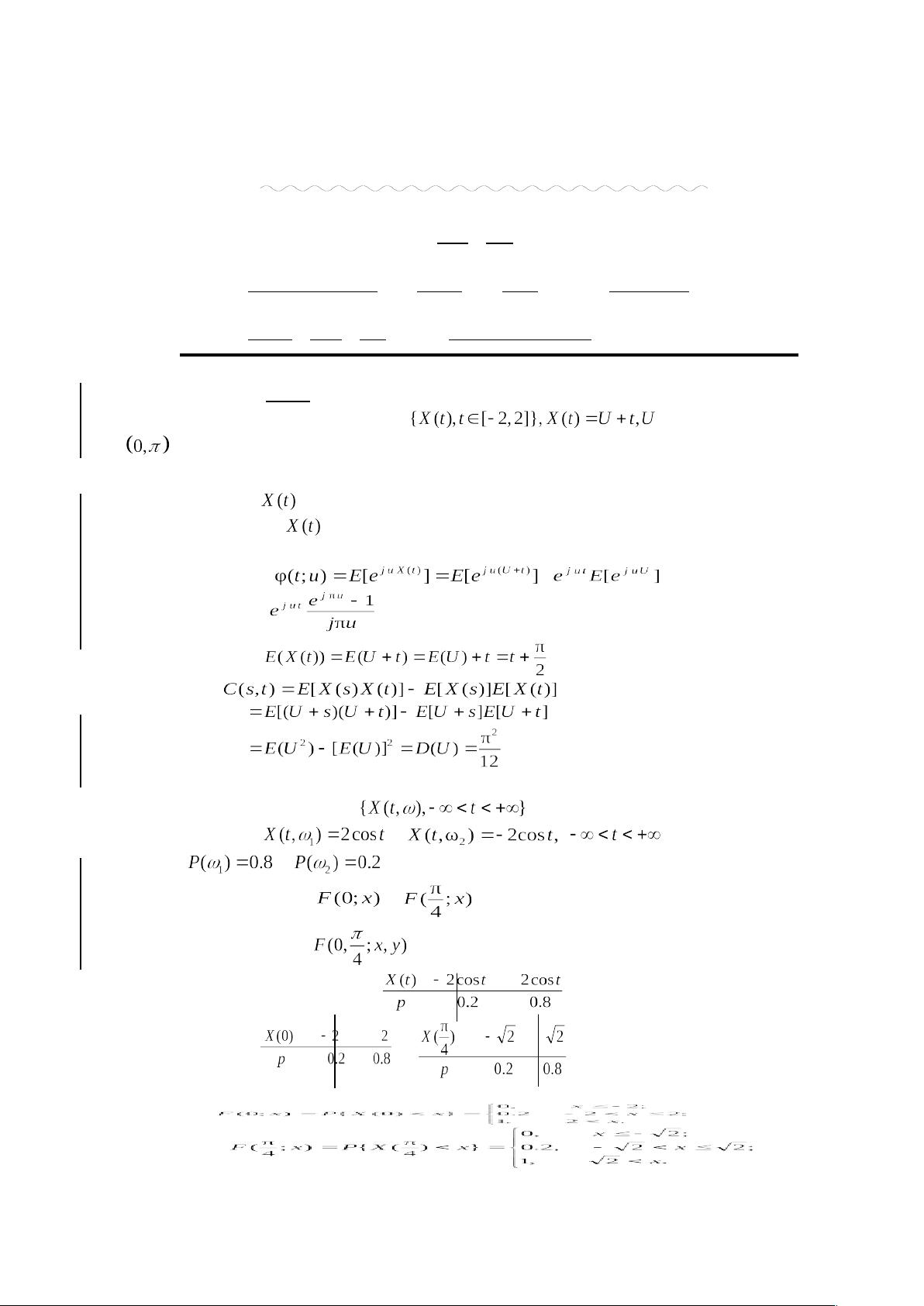
### 电子科技大学09应用随机过程试题解析 #### 一、题目分析与解答 本题主要考察了关于随机过程的基本概念及其性质。 1. **样本函数的理解与绘制** - **定义**: 随机过程的一个样本函数是指在某一确定的时间点上，随机过程的取值情况。 - **绘制**: 由于题目中的随机过程[pic]在[pic]上服从均匀分布，我们可以通过选取两个不同的时间点来描绘样本函数。例如，在时间[t1]和时间[t2]，随机变量[pic]的取值范围为[a, b]。这两个样本函数可以简单地通过直线段来表示，其中直线段位于[a, b]区间内。 2. **特征函数的求法** - 特征函数通常指的是随机变量的Fourier变换，对于随机过程[pic]来说，其特征函数可以通过积分的方式求得。根据题目给出的公式[pic]，我们可以得到特征函数的具体形式。这里的[pic]是时间的函数，而[pic]代表的是随机变量的均匀分布区间。 3. **均值函数与自协方差函数的计算** - **均值函数**: 均值函数是随机过程中每个时间点上的期望值。对于给定的随机过程[pic]，其均值函数[m(t)]可以通过计算随机变量[pic]的期望值来获得。 - **自协方差函数**: 自协方差函数反映了随机过程在不同时间点之间的统计相关性。计算[pic]的自协方差函数，需要先求出随机变量[pic]的方差，再利用随机过程的定义进行计算。 #### 二、题目分析与解答 该题进一步考察了随机过程的一维和二维分布函数。 1. **一维分布函数的计算** - 一维分布函数给出了随机过程在单个时间点上的概率分布。对于给定的随机过程，通过分析其样本函数，可以推导出在特定时间点上随机过程的可能取值范围，进而计算出相应的概率分布函数。 2. **二维分布函数的计算** - 二维分布函数则是指随机过程在两个不同时间点上的联合概率分布。通过给定的样本函数，可以构建出随机过程在两个时间点上同时处于某个取值区间的概率。 #### 三、题目分析与解答 此题考察了随机过程的均值函数与自协方差函数的计算方法。 1. **瑞利分布的应用** - 首先需要了解瑞利分布的基本特性，它是一种连续的概率分布，常用于描述信号幅度或噪声强度等物理现象。 - 给定随机变量[pic]服从瑞利分布，可以通过瑞利分布的密度函数来计算随机过程的均值函数。 2. **均值函数与自协方差函数的计算** - **均值函数**: 对于随机过程[pic]，其均值函数可以通过计算随机变量[pic]的期望值得到。 - **自协方差函数**: 计算自协方差函数时，需要考虑随机变量[pic]与时间变量t的关系以及它们之间的相互独立性。 #### 四、题目分析与解答 本题涉及到了泊松过程的应用。 1. **泊松过程的概率计算** - 泊松过程是一种重要的随机过程模型，常用来描述单位时间内事件发生的次数。题目要求计算在指定时间段内发生特定事件的概率。 - **第10位乘客到达的概率**: 通过泊松分布的累积分布函数可以求解。 - **平均时间间隔**: 泊松过程的平均时间间隔与过程的强度λ有关，可以通过1/λ来计算。 #### 五、题目分析与解答 此题探讨了宽平稳随机过程的相关概念。 1. **自相关函数的理解** - 自相关函数是描述随机过程统计性质的重要工具之一。宽平稳随机过程的自相关函数只与时间差τ有关，而不直接依赖于时间t。 2. **新随机过程的自相关函数计算** - 对于给定的宽平稳随机过程，通过数学变换构造出新的随机过程，并计算其自相关函数。 #### 六、题目分析与解答 该题考查了平稳独立增量过程和齐次马氏链的基本概念。 1. **平稳独立增量过程的概率计算** - 平稳独立增量过程意味着随机过程在不同时段内的增量相互独立，并且具有相同的分布。题目要求计算特定事件的概率。 2. **齐次马氏链的分析** - 齐次马氏链是一种特殊的随机过程，其中系统状态的变化仅依赖于当前状态，而不依赖于过去的历史。题目要求分析链的状态转移矩阵和概率转移图，并求出链的平稳分布。 #### 七、题目分析与解答 此题涉及齐次马氏链的高级应用。 1. **概率转移图的绘制** - 马氏链的概率转移图是描述系统状态转移的一种直观方式，通过概率转移图可以清晰地看到不同状态之间的转移路径和概率。 2. **二步转移矩阵的计算** - 二步转移矩阵是马氏链的重要概念，它描述了从当前状态经过两次状态转移后到达各个状态的概率。 3. **遍历性的判断与平稳分布的求解** - 遍历性是齐次马氏链的一个重要性质，如果一个马氏链是遍历的，则意味着在长时间运行下，系统将访问所有的状态，并且访问各个状态的概率将收敛到一个不变的值。题目要求判断给定的马氏链是否遍历，并求出其平稳分布。 #### 八、题目分析与解答 本题深入探讨了维纳过程和正态过程的性质。 1. **维纳过程的性质** - 维纳过程是一种重要的随机过程，具有平稳独立增量的特性。题目要求证明由维纳过程构造的新随机过程是严平稳的正态过程。 2. **正态过程的证明** - 为了证明一个随机过程是正态过程，需要验证其在任意有限多个时间点上的取值构成的向量都服从多维正态分布。题目通过构造随机向量并证明其为多维正态分布来完成这一证明。 本试题全面覆盖了随机过程的基础理论与应用实践，旨在检验考生对于随机过程概念的理解以及解决实际问题的能力。