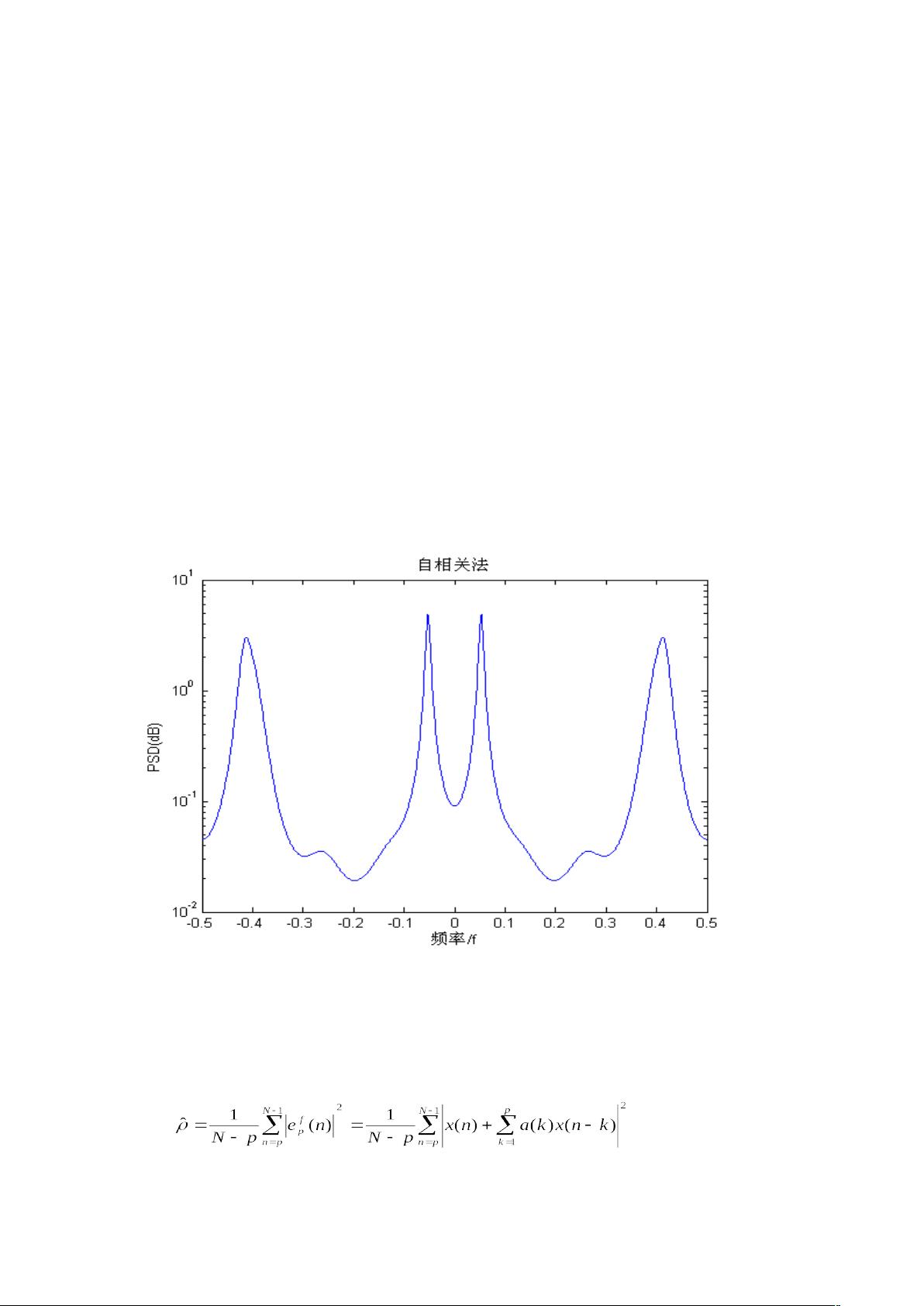
高级数字信号处理频谱估计访真程序

【高级数字信号处理频谱估计访真程序】是关于数字信号处理领域的一种实验技术，主要涉及频谱估计的各种方法，包括自相关法、协方差法、修正协方差法、伯格法以及MUSIC算法。这些方法在现代谱估计中用于分析和理解信号的频域特性。 1. **自相关法**： - 基本原理：自相关法，又称尤拉-沃克法，是通过估计自相关函数来确定AR模型参数。它利用最小化预测误差功率的方法，预测误差功率是基于观测数据无法观测部分为零的假设。自相关函数的估计通过计算样本的复共轭乘积之和得到，然后使用求复梯度的方法来找到最佳参数。这种方法的计算简化形式可以通过列文森递推公式得到，最后计算功率谱密度（PSD）。 - 算法程序：通过计算自相关序列`rxx`，构建 Toeplitz 矩阵并求逆，然后解线性系统获取AR参数，进而计算PSD。 - 仿真结果：自相关法的频率分辨率较低，不适合处理长数据序列，对于接近的频率成分难以区分。 2. **协方差法**： - 基本原理：与自相关法类似，但协方差法考虑了全部观测数据，无需填充零。同样采用最小化预测误差功率，但求和范围扩大至全部数据点。通过复梯度法求解AR参数。 - 算法程序：计算协方差矩阵`cxx`和中心协方差`cxx0`，然后解线性系统获取AR参数，计算PSD。 - 仿真结果：相比于自相关法，协方差法的频率分辨率更高，能更好地估计信号的频谱特性。 3. **修正协方差法**： - 基本原理：修正协方差法适用于长记录数据，通过平均前向和后向预测误差功率的最小化来估计AR参数，这使得在处理长序列时性能接近伯格法，但对短序列处理有所不同。 - 应用场景：在长数据记录中，修正协方差法与伯格法有相似的表现，而在短数据记录中，两者表现会有差异。 频谱估计的这些方法在实际应用中各有优缺点，例如自相关法计算简单但分辨率低，协方差法和修正协方差法则提供了更好的频率分辨率，适合处理更复杂的信号。伯格法和MUSIC算法（未详述）是另外两种高级的谱估计技术，通常用于高分辨率谱估计和噪声子空间估计，适用于检测弱信号或在强噪声环境中工作。 通过仿真实验，我们可以对比各种方法的性能，选择最适合特定应用的方法。在实际的数字信号处理系统中，选择合适的谱估计方法对于正确识别和分析信号的频谱特征至关重要。这些方法不仅应用于通信、雷达、声学和图像处理等领域，还对噪声抑制、信道估计、信号分离等任务具有重要意义。