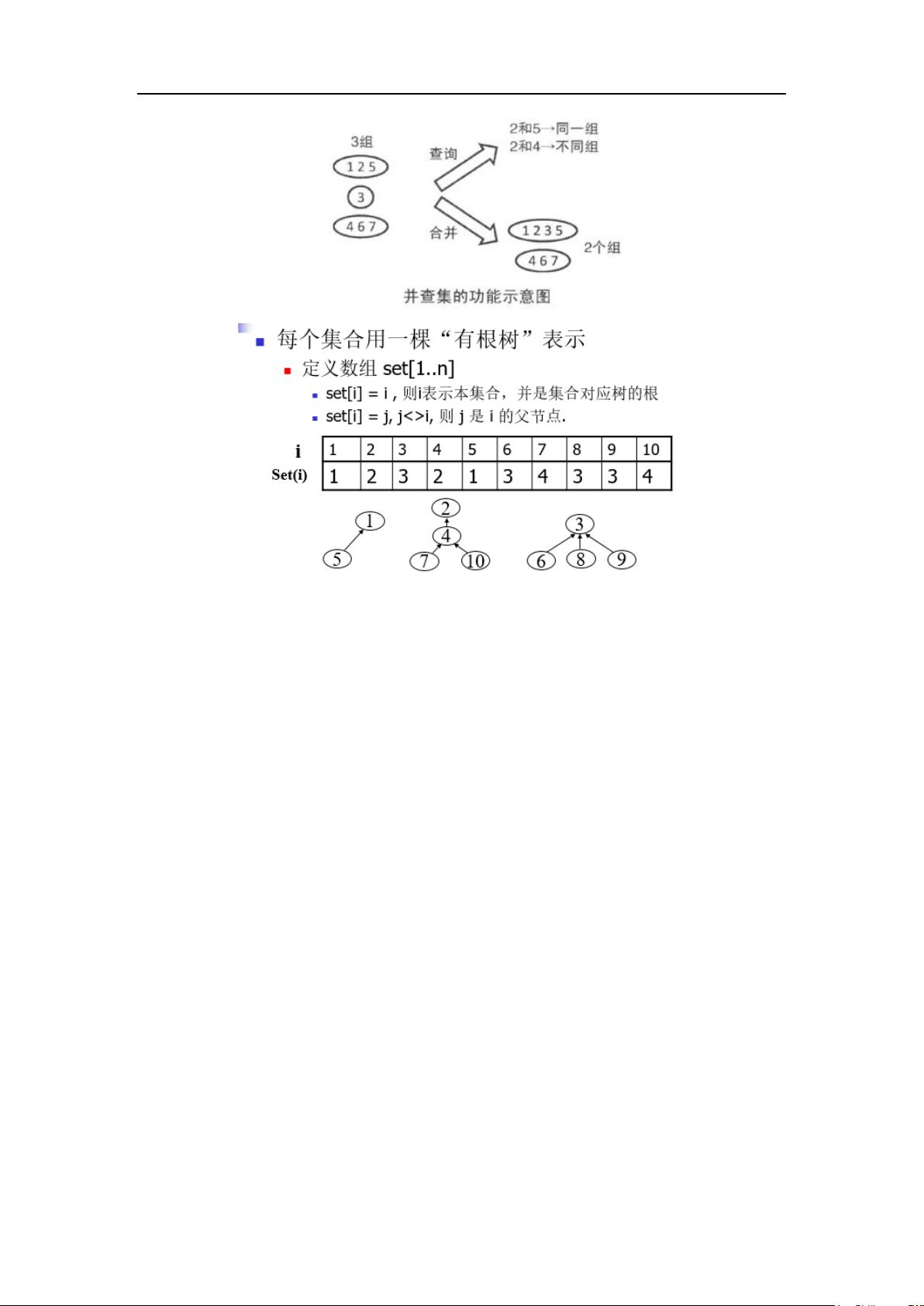
NOIP竞赛辅导专题CSP计算机等级考试辅导提高组普及组复赛辅导.pdf原创资料下载

NOIP竞赛辅导专题CSP计算机等级考试辅导提高组普及组复赛辅导.pdf原创资料下载，CSP考级，CSP非专业级别的能力认证，CSP考级辅导资料，算法入门资料，青少年编程集训资料，信息学奥赛，信息学奥林匹克竞赛，NOIP普及/提高组重新命名为CSP-J/S，NOIP普及组，CSP-S（提高级）对标到提高组。这样也可以就两轮比赛加以解释，即CSP-J1为普及组初赛，CSP-J2为普及组复赛，CSP-S1为提高组初赛，CSP-S2为提高组复赛。 ### NOIP竞赛辅导专题CSP计算机等级考试辅导提高组普及组复赛辅导 #### 一、各类数据范围 - **1.1 0x3F3F3F3F 的来源** - **INT 类型的最大值**： - `MAX = 0x7fffffff;` - `MIN = 0x80000000;` 或者 `MIN = -(1<<31);` - **十进制**：`MAX` 约为 2×10^9，如果数据超过 10^9，则需要使用 `long long` 类型进行存储。 - **使用 0x3F3F3F3F 的原因**： - 该值为十进制 1061109567，与 `0x7fffffff` 同一数量级（约 10^9），通常情况下，程序中的数据不会超过 10^9，因此可以将此值作为无穷大处理。 - 当与其它数值相加时，由于不超过 10^9，不会发生整数溢出。 - 使用 `memset(a,0x3f,sizeof(a));` 可以快速将数组初始化为无穷大。 - **1.2 数组可以开多大** - 没有绝对限制，但建议全局变量数组大小不超过 10^6，例如 `int a[1000000];`。 - 如果难以确定数组大小，可以考虑使用 `vector`，它可以根据实际需要动态调整大小。 #### 二、优化技巧 - **输入优化**： - 可以参考 [输入优化技巧](https://blog.csdn.net/Lj_victor/article/details/81590816)，提高程序读取数据的速度，这对于数据量较大的问题尤为重要。 #### 三、并查集 - **并查集简介**： - **基本操作**：主要包括**合并**（union）和**查找**（find）两个操作。 - **应用场景**：用于解决连通性问题，如判断两个元素是否在同一集合中、将两个集合合并等。 - **效率优化**：通过路径压缩和按秩合并等策略提高查找和合并操作的效率。 - **3.1 模板** - **简单并查集模板**： ```cpp const int MAXN = 1e6 + 10; int f[MAXN]; // 初始化 void init() { for (int i = 0; i < MAXN; i++) { f[i] = i; } } // 查找节点所属集合 int find(int x) { if (f[x] == x) return x; return f[x] = find(f[x]); // 路径压缩 } // 合并两个集合 void union_set(int a, int b) { int fa = find(a), fb = find(b); if (fa != fb) { f[fa] = fb; // 按秩合并可进一步优化 } } ``` #### 四、链式前向星 - **链式前向星简介**： - 一种用于存储图的数据结构，特别适合于存储稀疏图。 - 通过邻接表的方式存储每个顶点的相邻顶点，节省空间且便于遍历。 #### 五、STL - **STL 简介**： - **栈**（stack）：后进先出（LIFO）的线性数据结构。 - **队列**（queue）：先进先出（FIFO）的线性数据结构。 - **优先队列**（priority_queue）：支持插入元素和删除最高优先级元素。 - **双端队列**（deque）：两端均可进行插入和删除操作的队列。 - **map 容器**：键值对容器，支持基于键的快速查找。 - **string 操作**：字符串处理函数，如查找、替换、分割等。 - **vector 向量**：动态数组，自动管理内存。 - **set**：存储唯一元素的集合，支持快速查找。 #### 六、贪心算法 - **活动安排问题**： - 选择最早结束时间的活动进行安排，从而达到最大化活动数量的目的。 - **最小区间覆盖问题**： - 选择重叠最少的区间进行覆盖，使得覆盖所有点所需的区间数量最少。 - **练习题**：通过典型例题加深理解，提高解决问题的能力。 #### 七、归并排序 - **归并排序简介**： - 分治法的一种应用，将数组分成两半，递归地排序后再合并。 - 平均时间复杂度 O(nlogn)。 - **归并排序求逆序数**： - 在归并过程中统计逆序数的数量，可用于解决某些特殊问题。 #### 八、前缀和 - **前缀和简介**： - 用于加速计算区间和的操作，只需一次 O(n) 的预处理即可支持 O(1) 的区间和查询。 - **题目**：通过具体题目巩固前缀和的应用。 #### 九、差分数组 - **定义**： - 通过记录相邻元素之间的差值来间接表示整个数组。 - **性质**： - 支持快速更新区间元素的值。 - **例题**：利用差分数组解决实际问题。 #### 十、树状数组 - **简介**： - 也称为二叉索引树（Binary Indexed Tree），支持快速查询和更新单点或区间的操作。 - **实现**： - 通过低1位（lowbit）运算实现高效的区间查询和更新。 - **扩展**： - 可以通过扩展实现更复杂的功能，如二维树状数组。 - **练习题**：通过典型例题加深理解。 - **总结**：总结树状数组的特点及其适用场景。 #### 十一、字典树 - **字典树可以解决的问题**： - 字符串检索、单词计数等。 - **一题入门**：通过一个简单的例子介绍字典树的构建和使用。 - **练习题**：通过练习题深化理解。 #### 十二至十五、DP 入门、强化及优化 - **DP 入门**：介绍动态规划的基本概念和解题步骤。 - **强化**：深入探讨经典问题，如钱币找零问题。 - **优化**： - **二进制优化 DP**：利用二进制特性减少状态空间。 - **单调队列优化 DP**：适用于特定类型的子问题。 - **多路 DP**：处理多个维度的状态转移。 #### 十六至二十、高级数据结构与算法 - **区间 DP**：解决涉及区间的状态转移问题。 - **数位 DP**：用于处理数字串问题。 - **二分答案**：对于单调函数使用二分查找确定最优解。 - **二进制操作**：位运算技巧在算法中的应用。 - **状态压缩 DP**：使用二进制编码表示状态，减少状态空间。 #### 二十一至二十三、进阶主题 - **组合数学**：解决球盒问题、整数拆分等问题。 - **数论数学**：逆序数等数论概念在算法中的应用。 - **最优思想**： - **无序数组的最大差值**：寻找最大利润问题等。 - **期望/概率 DP**： - **概率模型**：基于概率分布的状态转移。 - **入门题目**：通过具体题目掌握基本概念。 - **赠券收集问题**：解决实际问题的应用。 - **高难度题目**：挑战更高难度的题目。 #### 二十四至二十五、总结与特殊技巧 - **DP 优化总结**：综合多种优化策略，提升解题效率。 - **单调栈**： - **简介**：单调栈的基本原理和实现方式。 - **应用**：如何在具体问题中使用单调栈。 - **练习题**：通过具体题目练习。 #### 二十六至二十八、数学与算法技巧 - **组合数学**： - **N 个球放入 M 个盒子问题**：经典的组合问题。 - **整数拆分**：将整数拆分为若干个数之和。 - **数论数学**：逆序数等概念的介绍。 - **最优思想**：无序数组的最大差值问题。 #### 二十九、数据结构 - 本章节涵盖了前面提到的各种数据结构，包括但不限于链式前向星、树状数组、字典树等，并提供了具体实例帮助理解每种数据结构的应用场景和实现细节。 以上内容全面介绍了从基础数据结构到高级算法的一系列知识点，旨在帮助读者系统地学习并掌握计算机科学领域的核心技能。通过这些知识点的学习，可以有效提高解决实际问题的能力，尤其是在信息学奥林匹克竞赛（NOIP）、CSP等比赛中取得好成绩。